Где в MQL4 / MQL5-реализации исходного родительского узла дерева C++ AVL возникает проблема?
Я не знаю, где у меня возникла проблема, но я получаю странную ошибку в моей реализации AVL, переведенную на MQL4/MQL5 язык.
В случае неудачи я попадаю в
- рекурсивно указывая на ту же проблему узла
или же
- отдельный узел без какого-либо родителя,
таким образом, балансируя, я сталкиваюсь с проблемой нулевого указателя.
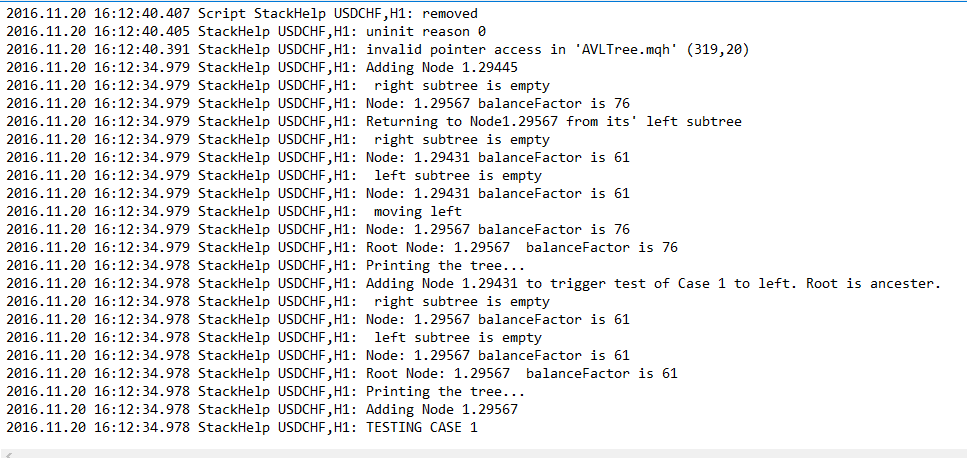
Тестовые случаи:
Копия / вставка терминала MetaTrader4/5 [ Journal ] находится ниже
Pass Case:
AVLTree *theAVLTree;
// Create a tree and test case 2
theAVLTree = new AVLTree();
Print("-----------------------------------------------");
Print("TESTING CASE 2");
// Add 50
Print("Adding Node 50");
theAVLTree.Insert(theAVLTree.CreateNewNode(50,4));
theAVLTree.PrintTree();
// Add 20
Print("Adding Node 20. Ancester's balance factor changes to L");
theAVLTree.Insert(theAVLTree.CreateNewNode(20,5));
theAVLTree.PrintTree();
// Add 70
Print("Adding Node 70 to trigger test of Case 2. Ancester's balance factor changes to =");
theAVLTree.Insert(theAVLTree.CreateNewNode(70,6));
theAVLTree.PrintTree();
// Add 90
Print("Adding Node 90. Ancester's balance factor changes to R.");
theAVLTree.Insert(theAVLTree.CreateNewNode(90,7));
theAVLTree.PrintTree();
// Add 15
Print("Adding Node 15 to trigger test of Case 2. Ancesters balance factor changes to =");
theAVLTree.Insert(theAVLTree.CreateNewNode(15,8));
theAVLTree.PrintTree();
Print("END TESTING CASE 2");
delete theAVLTree;
Print("-----------------------------------------------");
Print("-----------------------------------------------");
Неудачный случай:
AVLTree *theAVLTree;
//;;;;1.29397;1.29316;1.29259;1.29226;1.29298
// Test each case by adding some nodes to the tree then
// printing the tree after each insertion
// Create a tree and test case 1
theAVLTree = new AVLTree();
Print("TESTING CASE 1");
// Add 50
Print("Adding Node 1.29567");
theAVLTree.Insert(theAVLTree.CreateNewNode(1.29567,0));
theAVLTree.PrintTree();
// Add 20
Print("Adding Node 1.29431 to trigger test of Case 1 to left. Root is ancester.");
theAVLTree.Insert(theAVLTree.CreateNewNode(1.29431,1));
theAVLTree.PrintTree();
// Add 70
Print("Adding Node 1.29445");
theAVLTree.Insert(theAVLTree.CreateNewNode(1.29445,2));
theAVLTree.PrintTree();
// Add 90
Print("Adding Node 1.29433 to trigger test of Case 1 to right. Root is ancester.");
theAVLTree.Insert(theAVLTree.CreateNewNode(1.29433,3));
theAVLTree.PrintTree();
Print("END TESTING CASE 1");
delete theAVLTree;
Это MQL4/MQL5Код, но язык более или менее отражает CPP.
Исходный код для Cpp и заголовочного файла:
#property copyright "Copyright 2016, MetaQuotes Software Corp."
#property link "https://www.mql5.com"
#property strict
class AVLTreeNode
{
public:
double value;
int index;
// Other data fields can be inserted here
AVLTreeNode *left;
AVLTreeNode *right;
AVLTreeNode *parent;
char balanceFactor;
};
class AVLTree
{
private:
AVLTreeNode *root;
public:
AVLTree(); // Constructor
~AVLTree(); // Destructor
void Insert(AVLTreeNode *n);
void restoreAVL(AVLTreeNode *&ancestor, AVLTreeNode *&newNode);
void adjustBalanceFactors(AVLTreeNode *&end, AVLTreeNode *&_start);
void rotateLeft(AVLTreeNode *&n);
void rotateRight(AVLTreeNode *&n);
void adjustLeftRight(AVLTreeNode *&end, AVLTreeNode *&_start);
void adjustRightLeft(AVLTreeNode *&end, AVLTreeNode *&_start);
AVLTreeNode* CreateNewNode(double key,int index);
void PrintTree();
void FindNearest(double value,AVLTreeNode* &result[]);
private:
void ClearTree(AVLTreeNode *&n);
void Print(AVLTreeNode *&n);
AVLTreeNode* FindNearestHelper(AVLTreeNode* &pRoot, double value);
};
AVLTree::AVLTree()
{
root = NULL; // Initialize root to NULL
}
//------------------------------------------------------------------
// Class destructor
//------------------------------------------------------------------
AVLTree::~AVLTree()
{
// _start recursive destruction of tree
ClearTree(root);
}
//------------------------------------------------------------------
// ClearTree()
// Recursively delete all node in the tree.
//------------------------------------------------------------------
void AVLTree::ClearTree(AVLTreeNode *&n)
{
if(n != NULL)
{
ClearTree(n.left); // Recursively clear the left sub-tree
ClearTree(n.right); // Recursively clear the right sub-tree
delete n; // Delete this node
}
}
void AVLTree::Insert(AVLTreeNode *newNode)
{
AVLTreeNode *temp, *back, *ancestor;
temp = root;
back = NULL;
ancestor = NULL;
// Check for empty tree first
if(root == NULL)
{
root = newNode;
return;
}
// Tree is not empty so search for place to insert
while(temp != NULL) // Loop till temp falls out of the tree
{
back = temp;
// Mark ancestor that will be out of balance after
// this node is inserted
if(temp.balanceFactor != '=')
ancestor = temp;
if(newNode.value < temp.value)
temp = temp.left;
else
temp = temp.right;
}
// temp is now NULL
// back points to parent node to attach newNode to
// ancestor points to most recent out of balance ancestor
newNode.parent = back; // Set parent
if(newNode.value < back.value) // Insert at left
{
back.left = newNode;
}
else // Insert at right
{
back.right = newNode;
}
// Now call function to restore the tree's AVL property
restoreAVL(ancestor, newNode);
}
//------------------------------------------------------------------
// restoreAVL()
// Restore the AVL quality after inserting a new node.
// @param ancestor – most recent node back up the tree that is
// now out of balance.
// @param newNode– the newly inserted node.
//------------------------------------------------------------------
void AVLTree::restoreAVL(AVLTreeNode *&ancestor, AVLTreeNode *&newNode)
{
//--------------------------------------------------------------------------------
// Case 1: ancestor is NULL, i.e. balanceFactor of all ancestors' is '='
//--------------------------------------------------------------------------------
if(ancestor == NULL)
{
if(newNode.value < root.value) // newNode inserted to left of root
root.balanceFactor = 'L';
else
root.balanceFactor = 'R'; // newNode inserted to right of root
// Adjust the balanceFactor for all nodes from newNode back up to root
adjustBalanceFactors(root, newNode);
}
//--------------------------------------------------------------------------------
// Case 2: Insertion in opposite subtree of ancestor's balance factor, i.e.
// ancestor.balanceFactor = 'L' AND Insertion made in ancestor's right subtree
// OR
// ancestor.balanceFactor = 'R' AND Insertion made in ancestor's left subtree
//--------------------------------------------------------------------------------
else if(((ancestor.balanceFactor == 'L') && (newNode.value > ancestor.value)) ||
((ancestor.balanceFactor == 'R') && (newNode.value < ancestor.value)))
{
ancestor.balanceFactor = '=';
// Adjust the balanceFactor for all nodes from newNode back up to ancestor
adjustBalanceFactors(ancestor, newNode);
}
//--------------------------------------------------------------------------------
// Case 3: ancestor.balanceFactor = 'R' and the node inserted is
// in the right subtree of ancestor's right child
//--------------------------------------------------------------------------------
else if((ancestor.balanceFactor == 'R') && (newNode.value > ancestor.right.value))
{
ancestor.balanceFactor = '='; // Reset ancestor's balanceFactor
rotateLeft(ancestor); // Do single left rotation about ancestor
// Adjust the balanceFactor for all nodes from newNode back up to ancestor's parent
adjustBalanceFactors(ancestor.parent, newNode);
}
//--------------------------------------------------------------------------------
// Case 4: ancestor.balanceFactor is 'L' and the node inserted is
// in the left subtree of ancestor's left child
//--------------------------------------------------------------------------------
else if((ancestor.balanceFactor == 'L') && (newNode.value < ancestor.left.value))
{
ancestor.balanceFactor = '='; // Reset ancestor's balanceFactor
rotateRight(ancestor); // Do single right rotation about ancestor
// Adjust the balanceFactor for all nodes from newNode back up to ancestor's parent
adjustBalanceFactors(ancestor.parent, newNode);
}
//--------------------------------------------------------------------------------
// Case 5: ancestor.balanceFactor is 'L' and the node inserted is
// in the right subtree of ancestor's left child
//--------------------------------------------------------------------------------
else if((ancestor.balanceFactor == 'L') && (newNode.value > ancestor.left.value))
{
// Perform double right rotation (actually a left followed by a right)
rotateLeft(ancestor.left);
rotateRight(ancestor);
// Adjust the balanceFactor for all nodes from newNode back up to ancestor
adjustLeftRight(ancestor, newNode);
}
//--------------------------------------------------------------------------------
// Case 6: ancestor.balanceFactor is 'R' and the node inserted is
// in the left subtree of ancestor's right child
//--------------------------------------------------------------------------------
else
{
// Perform double left rotation (actually a right followed by a left)
rotateRight(ancestor.right);
rotateLeft(ancestor);
adjustRightLeft(ancestor, newNode);
}
}
//------------------------------------------------------------------
// Adjust the balance factor in all nodes from the inserted node's
// parent back up to but NOT including a designated end node.
// @param end– last node back up the tree that needs adjusting
// @param _start – node just inserted
//------------------------------------------------------------------
void AVLTree::adjustBalanceFactors(AVLTreeNode *&end, AVLTreeNode *&_start)
{
AVLTreeNode *temp = _start.parent; // Set _starting point at _start's parent
while(temp != end)
{
if(_start.value < temp.value)
temp.balanceFactor = 'L';
else
temp.balanceFactor = 'R';
temp = temp.parent;
} // end while
}
//------------------------------------------------------------------
// rotateLeft()
// Perform a single rotation left about n. This will rotate n's
// parent to become n's left child. Then n's left child will
// become the former parent's right child.
//------------------------------------------------------------------
void AVLTree::rotateLeft(AVLTreeNode *&n)
{
AVLTreeNode *temp = n.right; //Hold pointer to n's right child
n.right = temp.left; // Move temp 's left child to right child of n
if(temp.left != NULL) // If the left child does exist
temp .left.parent = n;// Reset the left child's parent
if(n.parent == NULL) // If n was the root
{
root = temp; // Make temp the new root
temp.parent = NULL; // Root has no parent
}
else if(n.parent.left == n) // If n was the left child of its' parent
n.parent.left = temp; // Make temp the new left child
else // If n was the right child of its' parent
n.parent.right = temp;// Make temp the new right child
if(temp!=n)
{
temp.left = n; // Move n to left child of temp
n.parent = temp; // Reset n's parent
}
}
//------------------------------------------------------------------
// rotateRight()
// Perform a single rotation right about n. This will rotate n's
// parent to become n's right child. Then n's right child will
// become the former parent's left child.
//------------------------------------------------------------------
void AVLTree::rotateRight(AVLTreeNode *&n)
{
AVLTreeNode *temp = n.left; //Hold pointer to temp
n.left = temp.right; // Move temp's right child to left child of n
if(temp.right != NULL) // If the right child does exist
temp.right.parent = n; // Reset right child's parent
if(n.parent == NULL) // If n was root
{
root = temp; // Make temp the root
temp.parent = NULL; // Root has no parent
}
else if(n.parent.left == n) // If was the left child of its' parent
n.parent.left = temp; // Make temp the new left child
else // If n was the right child of its' parent
n.parent.right = temp; // Make temp the new right child
temp.right = n; // Move n to right child of temp
n.parent = temp; // Reset n's parent
}
//------------------------------------------------------------------
// adjustLeftRight()
// @param end- last node back up the tree that needs adjusting
// @param _start - node just inserted
//------------------------------------------------------------------
void AVLTree::adjustLeftRight(AVLTreeNode *&end, AVLTreeNode *&_start)
{
if(end == root)
end.balanceFactor = '=';
else if(_start.value < end.parent.value)
{
end.balanceFactor = 'R';
adjustBalanceFactors(end.parent.left, _start);
}
else
{
end.balanceFactor = '=';
end.parent.left.balanceFactor = 'L';
adjustBalanceFactors(end, _start);
}
}
//------------------------------------------------------------------
// adjustRightLeft
// @param end- last node back up the tree that needs adjusting
// @param _start - node just inserted
//------------------------------------------------------------------
void AVLTree::adjustRightLeft(AVLTreeNode *&end, AVLTreeNode *&_start)
{
if(end == root)
end.balanceFactor = '=';
else if(_start.value > end.parent.value)
{
end.balanceFactor = 'L';
adjustBalanceFactors(end.parent.right, _start);
}
else
{
end.balanceFactor = '=';
end.parent.right.balanceFactor = 'R';
adjustBalanceFactors(end, _start);
}
}
//------------------------------------------------------------------
// PrintTree()
// Intiate a recursive traversal to print the tree
//------------------------------------------------------------------
void AVLTree::PrintTree()
{
Print("Printing the tree...");
Print("Root Node: "+ string(root.value) +" balanceFactor is "+string(root.balanceFactor));
Print(root);
}
//------------------------------------------------------------------
// Print()
// Perform a recursive traversal to print the tree
//------------------------------------------------------------------
void AVLTree::Print(AVLTreeNode *&n)
{
if(n != NULL)
{
Print("Node: "+ string(n.value) + " balanceFactor is "+ string(n.balanceFactor) + "");
if(n.left != NULL)
{
Print(" moving left");
Print(n.left);
Print("Returning to Node"+ string(n.value) + " from its' left subtree");
}
else
{
Print(" left subtree is empty");
}
Print("Node: "+ string(n.value) + " balanceFactor is "+ string(n.balanceFactor) + "");
if(n.right != NULL)
{
Print(" moving right");
Print(n.right);
Print("Returning to Node "+ string(n.value) + " from its' right subtree");
}
else
{
Print(" right subtree is empty");
}
}
}
AVLTreeNode* AVLTree::FindNearestHelper(AVLTreeNode* &pRoot, double value)
{
AVLTreeNode* pClosest = NULL;
double minDistance = 1.7976931348623159*MathPow(10,308); // = DBL_MAX; // SYSTEM CONST
AVLTreeNode* pNode = pRoot;
while(pNode != NULL){
double distance = MathAbs(pNode.value - value);
if(distance < minDistance){
minDistance = distance;
pClosest = pNode;
}
if(distance == 0)
break;
if(pNode.value > value)
pNode = pNode.left;
else if(pNode.value < value)
pNode = pNode.right;
}
return pClosest;
}
void AVLTree::FindNearest(double value,AVLTreeNode* &result[])
{
AVLTreeNode* nearest= FindNearestHelper(root,value);
if(nearest!=NULL)
{
int rSize=0;
rSize=rSize+1;
ArrayResize(result,rSize);
result[rSize-1]=nearest;
AVLTreeNode* nParent=nearest.parent;
AVLTreeNode* nLeft=nearest.left;
AVLTreeNode* nRight=nearest.right;
if(nearest.value>value)
{
if(nLeft!=NULL) nearest=nLeft;
else nearest=nParent;
}
else
{
if(nRight!=NULL)nearest=nRight;
else nearest=nParent;
}
if(nearest!=NULL)
{
rSize=rSize+1;
ArrayResize(result,rSize);
result[rSize-1]=nearest;
}
}
}
//---------------------------------------------
// Create a new tree node with the given key
//---------------------------------------------
AVLTreeNode* AVLTree::CreateNewNode(double key,int ind)
{
AVLTreeNode *temp = new AVLTreeNode();
temp.index = ind;
temp.value = key;
temp.left = NULL;
temp.right = NULL;
temp.parent = NULL;
temp.balanceFactor = '=';
return temp;
}
Более подробная информация в соответствии с запросом: Test MQL Script:
//+------------------------------------------------------------------+
//| StackHelp.mq4 |
//| Copyright 2016, MetaQuotes Software Corp. |
//| https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2016, MetaQuotes Software Corp."
#property link "https://www.mql5.com"
#property version "1.00"
#property strict
#include <Custom\AVLTree.mqh>
//+
//+------------------------------------------------------------------+
//| Script program start function |
//+------------------------------------------------------------------+
void OnStart()
{
//---
AVLTree *theAVLTree;
theAVLTree = new AVLTree();
Print("TESTING CASE 1");
// Add 1.29567
Print("Adding Node 1.29567");
theAVLTree.Insert(theAVLTree.CreateNewNode(1.29567,0));
theAVLTree.PrintTree();
// Add 1.29431
Print("Adding Node 1.29431 to trigger test of Case 1 to left. Root is ancester.");
theAVLTree.Insert(theAVLTree.CreateNewNode(1.29431,1));
theAVLTree.PrintTree();
// Add 1.29445
Print("Adding Node 1.29445");
theAVLTree.Insert(theAVLTree.CreateNewNode(1.29445,2));
theAVLTree.PrintTree();
// Add 1.2943
Print("Adding Node 1.29433 to trigger test of Case 1 to right. Root is ancester.");
theAVLTree.Insert(theAVLTree.CreateNewNode(1.29433,3));
theAVLTree.PrintTree();
Print("END TESTING CASE 1");
delete theAVLTree;
Print("END TESTING CASE 1");
delete theAVLTree;
}
1 ответ
Мой подозреваемый - асимметрия в :rotateLeft() против :rotateRight() класс-метода.
Первый содержит избегание сингулярности / циркулярных ссылок, второй - нет.
void AVLTree::rotateLeft( AVLTreeNode *&n )
{
AVLTreeNode *temp = n.right; // Hold pointer to n's right child
n.right = temp.left; // Move temp 's left child to right child of n
if ( temp.left != NULL ) // If the left child does exist
temp.left.parent = n; // Reset the left child's parent
if ( n.parent == NULL ) // If n was the root
{ root = temp; // Make temp the new root
temp.parent = NULL; // Root has no parent
}
else if ( n.parent.left == n ) // If n was the left child of its' parent
n.parent.left = temp; // Make temp the new left child
else // If n was the right child of its' parent
n.parent.right = temp; // Make temp the new right child
if ( temp != n ) // If !n ( avoid ( n.parent == n ) + ( n.left == n ) singularities / circulars )
{
temp.left = n; // Move n to left child of temp
n.parent = temp; // Reset n's parent
}
}
+ несколько крошечных деталей, прокомментированных ниже:
#property copyright "Copyright 2016, VyshuRam, VOLVO.COM"
#property link "https://www.volvo.com"
#property strict
class AVLTreeNode
{
public:
double value;
int index;
// ---------------------------------- // Other data fields can be inserted here
AVLTreeNode* left;
AVLTreeNode* right;
AVLTreeNode* parent;
char balanceFactor;
};
class AVLTree
{
private:
AVLTreeNode* root;
public:
AVLTree(); // Constructor
~AVLTree(); // Destructor
void Insert( AVLTreeNode* n );
void restoreAVL( AVLTreeNode* &ancestor,
AVLTreeNode* &newNode
);
void adjustBalanceFactors( AVLTreeNode* &end,
AVLTreeNode* &_start
);
void rotateLeft( AVLTreeNode* &n );
void rotateRight( AVLTreeNode* &n );
void adjustLeftRight( AVLTreeNode* &end,
AVLTreeNode* &_start
);
void adjustRightLeft( AVLTreeNode* &end,
AVLTreeNode* &_start
);
AVLTreeNode* CreateNewNode( double key,
int index );
void PrintTree();
void FindNearest( double value,
AVLTreeNode* &result[]
);
private:
void ClearTree( AVLTreeNode* &n );
void Print( AVLTreeNode* &n );
AVLTreeNode* FindNearestHelper( AVLTreeNode* &pRoot,
double value
);
};
AVLTree::AVLTree()
{
root = NULL; // Initialize root to NULL
}
//------------------------------------------------------------------
// Class destructor
//------------------------------------------------------------------
AVLTree::~AVLTree()
{
ClearTree( root ); // start recursive destruction of tree
}
//------------------------------------------------------------------
// ClearTree()
// Recursively delete all node in the tree.
//------------------------------------------------------------------
void AVLTree::ClearTree( AVLTreeNode *&n )
{
if ( n != NULL )
{
ClearTree( n.left ); // Recursively clear the left sub-tree
ClearTree( n.right ); // Recursively clear the right sub-tree
delete n; // Delete this node
}
}
void AVLTree::Insert( AVLTreeNode *newNode )
{
AVLTreeNode *temp, *back, *ancestor;
temp = root;
back = NULL;
ancestor = NULL;
if ( root == NULL ) // Check for empty tree first
{
root = newNode;
return;
}
// // Tree is not empty so search for place to insert
while ( temp != NULL ) // Loop till temp falls out of the tree
{
back = temp; // begins with temp == root
// Mark ancestor that will be out of balance after this node is inserted
if ( temp.balanceFactor != '=' ) ancestor = temp;
if ( newNode.value < temp.value ) temp = temp.left;
else temp = temp.right;
}
// temp is now NULL ( while(){..}-terminated )
// back points to parent node to attach a newNode to
// ancestor points to most recent out of balance ancestor
newNode.parent = back; // Set parent
if ( newNode.value < back.value ) // Insert at left
{
back.left = newNode;
}
else // Insert at right
{
back.right = newNode;
}
// Now call function to restore the tree's AVL property
restoreAVL( ancestor, newNode );
}
//------------------------------------------------------------------
// restoreAVL()
// Restore the AVL quality after inserting a new node.
// @param ancestor – most recent node back up the tree that is
// now out of balance.
// @param newNode– the newly inserted node.
//------------------------------------------------------------------
void AVLTree::restoreAVL( AVLTreeNode *&ancestor, AVLTreeNode *&newNode )
{
//--------------------------------------------------------------------------------
// Case 1: ancestor is NULL, i.e. balanceFactor of all ancestors' is '='
//--------------------------------------------------------------------------------
if ( ancestor == NULL )
{
if ( newNode.value < root.value )
root.balanceFactor = 'L'; // newNode inserted to left of root
else root.balanceFactor = 'R'; // newNode inserted to right of root
adjustBalanceFactors( root, // Adjust the balanceFactor
newNode // for all nodes
); // from newNode back up to root
}
//--------------------------------------------------------------------------------
// Case 2: Insertion in opposite subtree of ancestor's balance factor, i.e.
// ancestor.balanceFactor = 'L' AND Insertion made in ancestor's right subtree
// OR
// ancestor.balanceFactor = 'R' AND Insertion made in ancestor's left subtree
//--------------------------------------------------------------------------------
else if ( ( ( ancestor.balanceFactor == 'L' )
&& ( ancestor.value < newNode.value )
)
|| ( ( ancestor.balanceFactor == 'R' )
&& ( ancestor.value > newNode.value )
)
)
{
ancestor.balanceFactor = '=';
adjustBalanceFactors( ancestor, // Adjust the balanceFactor
newNode // for all nodes
); // from newNode back up to ancestor
}
//--------------------------------------------------------------------------------
// Case 3: ancestor.balanceFactor = 'R' and the node inserted is
// in the right subtree of ancestor's right child
//--------------------------------------------------------------------------------
else if ( ( ancestor.balanceFactor == 'R' )
&& ( ancestor.right.value < newNode.value )
)
{
ancestor.balanceFactor = '='; // Reset ancestor's balanceFactor
rotateLeft( ancestor ); // Do single left rotation about ancestor
adjustBalanceFactors( ancestor.parent, // Adjust the balanceFactor
newNode // for all nodes
); // from newNode back up to ancestor's parent
}
//--------------------------------------------------------------------------------
// Case 4: ancestor.balanceFactor is 'L' and the node inserted is
// in the left subtree of ancestor's left child
//--------------------------------------------------------------------------------
else if ( ( ancestor.balanceFactor == 'L' )
&& ( ancestor.left.value > newNode.value )
)
{
ancestor.balanceFactor = '='; // Reset ancestor's balanceFactor
rotateRight( ancestor ); // Do single right rotation about ancestor
adjustBalanceFactors( ancestor.parent, // Adjust the balanceFactor
newNode // for all nodes
); // from newNode back up to ancestor's parent
}
//--------------------------------------------------------------------------------
// Case 5: ancestor.balanceFactor is 'L' and the node inserted is
// in the right subtree of ancestor's left child
//--------------------------------------------------------------------------------
else if ( ( ancestor.balanceFactor == 'L' )
&& ( ancestor.left.value < newNode.value )
)
{
rotateLeft( ancestor.left ); // Perform double right rotation
rotateRight( ancestor ); // (actually a left followed by a right)
adjustLeftRight( ancestor, // Adjust the balanceFactor
newNode // for all nodes
); // from newNode back up to ancestor
}
//--------------------------------------------------------------------------------
// Case 6: ancestor.balanceFactor is 'R' and the node inserted is
// in the left subtree of ancestor's right child
//--------------------------------------------------------------------------------
else
{
rotateRight( ancestor.right ); // Perform double left rotation
rotateLeft( ancestor ); // (actually a right followed by a left)
adjustRightLeft( ancestor, // Adjust the balanceFactor
newNode // for all nodes
); // from newNode back up to ancestor
}
}
//------------------------------------------------------------------
// Adjust the balance factor in all nodes from the inserted node's
// parent back up to but NOT including a designated end node.
// @param end– last node back up the tree that needs adjusting
// @param _start – node just inserted
//------------------------------------------------------------------
void AVLTree::adjustBalanceFactors( AVLTreeNode *&end, AVLTreeNode *&_start )
{
AVLTreeNode *temp = _start.parent; // Set _starting point at _start's parent
while ( temp != end )
{
if ( _start.value < temp.value ) temp.balanceFactor = 'L';
else temp.balanceFactor = 'R';
temp = temp.parent;
} // end while
}
//------------------------------------------------------------------
// rotateLeft()
// Perform a single rotation left about n. This will rotate n's
// parent to become n's left child. Then n's left child will
// become the former parent's right child.
//------------------------------------------------------------------
void AVLTree::rotateLeft( AVLTreeNode *&n )
{
AVLTreeNode *temp = n.right; // Hold pointer to n's right child
n.right = temp.left; // Move temp 's left child to right child of n
if ( temp.left != NULL ) // If the left child does exist
temp.left.parent = n; // Reset the left child's parent
if ( n.parent == NULL ) // If n was the root
{ root = temp; // Make temp the new root
temp.parent = NULL; // Root has no parent
}
else if ( n.parent.left == n ) // If n was the left child of its' parent
n.parent.left = temp; // Make temp the new left child
else // If n was the right child of its' parent
n.parent.right = temp; // Make temp the new right child
if ( temp != n ) // If !n ( avoid ( n.parent == n ) + ( n.left == n ) singularities / circulars )
{
temp.left = n; // Move n to left child of temp
n.parent = temp; // Reset n's parent
}
}
//------------------------------------------------------------------
// rotateRight()
// Perform a single rotation right about n. This will rotate n's
// parent to become n's right child. Then n's right child will
// become the former parent's left child.
//------------------------------------------------------------------
void AVLTree::rotateRight( AVLTreeNode *&n )
{
AVLTreeNode *temp = n.left; // Hold pointer to temp
n.left = temp.right; // Move temp's right child to left child of n
if ( temp.right != NULL ) // If the right child does exist
temp.right.parent = n; // Reset right child's parent
if ( n.parent == NULL ) // If n was root
{ root = temp; // Make temp the root
temp.parent = NULL; // Root has no parent
}
else if ( n.parent.left == n ) // If was the left child of its' parent
n.parent.left = temp; // Make temp the new left child
else // If n was the right child of its' parent
n.parent.right = temp; // Make temp the new right child
temp.right = n; // Move n to right child of temp
n.parent = temp; // Reset n's parent
}
//------------------------------------------------------------------
// adjustLeftRight()
// @param end- last node back up the tree that needs adjusting
// @param _start - node just inserted
//------------------------------------------------------------------
void AVLTree::adjustLeftRight( AVLTreeNode *&end,
AVLTreeNode *&_start
)
{
if ( end == root )
end.balanceFactor = '=';
else if ( _start.value < end.parent.value )
{
end.balanceFactor = 'R';
adjustBalanceFactors( end.parent.left, _start );
}
else
{
end.balanceFactor = '=';
end.parent.left.balanceFactor = 'L';
adjustBalanceFactors( end, _start );
}
}
//------------------------------------------------------------------
// adjustRightLeft
// @param end- last node back up the tree that needs adjusting
// @param _start - node just inserted
//------------------------------------------------------------------
void AVLTree::adjustRightLeft( AVLTreeNode *&end,
AVLTreeNode *&_start
)
{
if ( end == root )
end.balanceFactor = '=';
else if ( _start.value > end.parent.value )
{
end.balanceFactor = 'L';
adjustBalanceFactors( end.parent.right, _start );
}
else
{
end.balanceFactor = '=';
end.parent.right.balanceFactor = 'R';
adjustBalanceFactors( end, _start );
}
}
//------------------------------------------------------------------
// PrintTree()
// Intiate a recursive traversal to print the tree
//------------------------------------------------------------------
void AVLTree::PrintTree()
{
Print( "Printing the tree..." );
Print( "Root Node: " + string( root.value ) +" balanceFactor is " + string( root.balanceFactor ) );
Print( root );
}
//------------------------------------------------------------------
// Print()
// Perform a recursive traversal to print the tree
//------------------------------------------------------------------
void AVLTree::Print( AVLTreeNode *&n )
{
if ( n != NULL )
{
Print( "Node: " + string( n.value ) + " balanceFactor is "+ string( n.balanceFactor ) + "" );
if ( n.left != NULL )
{
Print( " moving left" );
Print( n.left );
Print( "Returning to Node" + string( n.value ) + " from its' left subtree" );
}
else
{
Print( " left subtree is empty" );
}
Print( "Node: " + string( n.value ) + " balanceFactor is " + string( n.balanceFactor ) + "" );
if ( n.right != NULL )
{
Print( " moving right" );
Print( n.right );
Print( "Returning to Node " + string( n.value ) + " from its' right subtree" );
}
else
{
Print( " right subtree is empty" );
}
}
}
AVLTreeNode* AVLTree::FindNearestHelper( AVLTreeNode* &pRoot, double value )
{
AVLTreeNode* pClosest = NULL;
double minDistance = 1.7976931348623159 * MathPow( 10, 308 ); // = DBL_MAX; // SYSTEM CONST
AVLTreeNode* pNode = pRoot;
while ( pNode != NULL ){
double distance = MathAbs( pNode.value - value );
if ( minDistance > distance ){
minDistance = distance;
pClosest = pNode;
}
if ( distance == 0 ) break;
if ( pNode.value > value ) pNode = pNode.left;
else if ( pNode.value < value ) pNode = pNode.right;
}
return pClosest;
}
void AVLTree::FindNearest( double value, AVLTreeNode* &result[] )
{
AVLTreeNode* nearest= FindNearestHelper( root, value );
if ( nearest != NULL )
{
int rSize = 0; // ?| rSize = 1; ...........
rSize = rSize + 1; // ?|
ArrayResize( result, rSize );
result[rSize-1] = nearest;
AVLTreeNode* nParent = nearest.parent;
AVLTreeNode* nLeft = nearest.left;
AVLTreeNode* nRight = nearest.right;
if ( nearest.value > value )
{
if ( nLeft != NULL ) nearest = nLeft;
else nearest = nParent;
}
else
{
if ( nRight != NULL ) nearest = nRight;
else nearest = nParent;
}
if ( nearest != NULL )
{
rSize = rSize + 1;
ArrayResize( result, rSize );
result[rSize-1] = nearest;
}
}
}
//---------------------------------------------
// Create a new tree node with the given key
//---------------------------------------------
AVLTreeNode* AVLTree::CreateNewNode( double key,int ind )
{
AVLTreeNode *temp = new AVLTreeNode();
temp.index = ind;
temp.value = key;
temp.left = NULL;
temp.right = NULL;
temp.parent = NULL;
temp.balanceFactor = '=';
return temp;
}