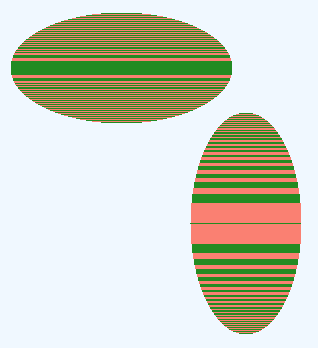Region.IsVisible(PointF) имеет очень низкую производительность для больших значений с плавающей запятой
У меня возникла странная проблема с производительностью, и было бы здорово, если бы я объяснил поведение, которое я испытываю.
Я использую System.Drawing.Region.IsVisible(PointF), чтобы определить, находится ли точка внутри многоугольника. Обычно это работает очень хорошо, но вчера я заметил, что производительность метода IsVisible становится очень медленной, если многоугольник сложный и состоит из больших значений x и y.
Ниже приведен код для воспроизведения проблемы (и изображение, которое показывает форму многоугольника), извините за большой размер массива, но многоугольник должен быть довольно сложным, прежде чем возникнет проблема.
При вызове IsVisible для исходных точек моей машине для завершения требуется 460 651 миллисекунд, тогда как когда я сначала делю все точки на 1000, а затем вызываю метод, это занимает 1 миллисекунду. Почему я вижу такую большую разницу во времени? Я не думал, что фактические значения с плавающей точкой будут влиять на производительность.
using System;
using System.Diagnostics;
using System.Drawing;
using System.Drawing.Drawing2D;
using System.Linq;
namespace PerformanceTest
{
class Program
{
static void Main(string[] args)
{
// Create complex polygon with large x and y values
float[] xValues = {1.014498E+07f, 1.016254E+07f, 1.019764E+07f, 1.021519E+07f, 1.023274E+07f, 1.026785E+07f, 1.026785E+07f, 1.02854E+07f, 1.02854E+07f, 1.030295E+07f, 1.03205E+07f, 1.033805E+07f, 1.035561E+07f, 1.037316E+07f, 1.039071E+07f, 1.040826E+07f, 1.042581E+07f, 1.044337E+07f, 1.046092E+07f, 1.047847E+07f, 1.049602E+07f, 1.051357E+07f, 1.054868E+07f, 1.056623E+07f, 1.058378E+07f, 1.060133E+07f, 1.061888E+07f, 1.061888E+07f, 1.063644E+07f, 1.065399E+07f, 1.068909E+07f, 1.068909E+07f, 1.070664E+07f, 1.07242E+07f, 1.074175E+07f, 1.074175E+07f, 1.07593E+07f, 1.07593E+07f, 1.077685E+07f, 1.07944E+07f, 1.07944E+07f, 1.081196E+07f, 1.081196E+07f, 1.081196E+07f, 1.082951E+07f, 1.084706E+07f, 1.084706E+07f, 1.086461E+07f, 1.086461E+07f, 1.088216E+07f, 1.089971E+07f, 1.091727E+07f, 1.093482E+07f, 1.098747E+07f, 1.100503E+07f, 1.102258E+07f, 1.104013E+07f, 1.105768E+07f, 1.107523E+07f, 1.107523E+07f, 1.109279E+07f, 1.109279E+07f, 1.109279E+07f, 1.109279E+07f, 1.109279E+07f, 1.111034E+07f, 1.111034E+07f, 1.111034E+07f, 1.111034E+07f, 1.111034E+07f, 1.112789E+07f, 1.112789E+07f, 1.112789E+07f, 1.114544E+07f, 1.116299E+07f, 1.118054E+07f, 1.11981E+07f, 1.12332E+07f, 1.125075E+07f, 1.12683E+07f, 1.128586E+07f, 1.130341E+07f, 1.135606E+07f, 1.137361E+07f, 1.139117E+07f, 1.140872E+07f, 1.144382E+07f, 1.146137E+07f, 1.147893E+07f, 1.149648E+07f, 1.151403E+07f, 1.153158E+07f, 1.154913E+07f, 1.156669E+07f, 1.156669E+07f, 1.158424E+07f, 1.158424E+07f, 1.158424E+07f, 1.158424E+07f, 1.158424E+07f, 1.158424E+07f, 1.158424E+07f, 1.158424E+07f, 1.158424E+07f, 1.158424E+07f, 1.158424E+07f, 1.156669E+07f, 1.156669E+07f, 1.151403E+07f, 1.149648E+07f, 1.149648E+07f, 1.149648E+07f, 1.149648E+07f, 1.149648E+07f, 1.149648E+07f, 1.149648E+07f, 1.149648E+07f, 1.149648E+07f, 1.153158E+07f, 1.154913E+07f, 1.156669E+07f, 1.156669E+07f, 1.158424E+07f, 1.160179E+07f, 1.160179E+07f, 1.161934E+07f, 1.165444E+07f, 1.1672E+07f, 1.168955E+07f, 1.17071E+07f, 1.172465E+07f, 1.17422E+07f, 1.175976E+07f, 1.177731E+07f, 1.179486E+07f, 1.181241E+07f, 1.182996E+07f, 1.184752E+07f, 1.186507E+07f, 1.188262E+07f, 1.190017E+07f, 1.190017E+07f, 1.191772E+07f, 1.191772E+07f, 1.193528E+07f, 1.193528E+07f, 1.193528E+07f, 1.193528E+07f, 1.193528E+07f, 1.193528E+07f, 1.193528E+07f, 1.193528E+07f, 1.193528E+07f, 1.193528E+07f, 1.193528E+07f, 1.193528E+07f, 1.193528E+07f, 1.193528E+07f, 1.193528E+07f, 1.193528E+07f, 1.193528E+07f, 1.193528E+07f, 1.193528E+07f, 1.193528E+07f, 1.195283E+07f, 1.197038E+07f, 1.198793E+07f, 1.200548E+07f, 1.202303E+07f, 1.204059E+07f, 1.205814E+07f, 1.207569E+07f, 1.209324E+07f, 1.211079E+07f, 1.212835E+07f, 1.21459E+07f, 1.216345E+07f, 1.2181E+07f, 1.219855E+07f, 1.221611E+07f, 1.221611E+07f, 1.223366E+07f, 1.225121E+07f, 1.226876E+07f, 1.226876E+07f, 1.228631E+07f, 1.230386E+07f, 1.230386E+07f, 1.230386E+07f, 1.232142E+07f, 1.232142E+07f, 1.232142E+07f, 1.232142E+07f, 1.232142E+07f, 1.232142E+07f, 1.232142E+07f, 1.232142E+07f, 1.235652E+07f, 1.235652E+07f, 1.237407E+07f, 1.237407E+07f, 1.239162E+07f, 1.239162E+07f, 1.240918E+07f, 1.242673E+07f, 1.242673E+07f, 1.244428E+07f, 1.247938E+07f, 1.249694E+07f, 1.251449E+07f, 1.253204E+07f, 1.254959E+07f, 1.256714E+07f, 1.258469E+07f, 1.260225E+07f, 1.263735E+07f, 1.26549E+07f, 1.267245E+07f, 1.269001E+07f, 1.270756E+07f, 1.272511E+07f, 1.272511E+07f, 1.274266E+07f, 1.274266E+07f, 1.276021E+07f, 1.276021E+07f, 1.277776E+07f, 1.277776E+07f, 1.277776E+07f, 1.277776E+07f, 1.279532E+07f, 1.279532E+07f, 1.279532E+07f, 1.281287E+07f, 1.281287E+07f, 1.281287E+07f, 1.281287E+07f, 1.281287E+07f, 1.281287E+07f, 1.281287E+07f, 1.281287E+07f, 1.281287E+07f, 1.281287E+07f, 1.281287E+07f, 1.281287E+07f, 1.281287E+07f, 1.281287E+07f, 1.281287E+07f, 1.279532E+07f, 1.277776E+07f, 1.276021E+07f, 1.276021E+07f, 1.274266E+07f, 1.274266E+07f, 1.272511E+07f, 1.272511E+07f, 1.272511E+07f, 1.274266E+07f, 1.276021E+07f, 1.279532E+07f, 1.281287E+07f, 1.283042E+07f, 1.284797E+07f, 1.286552E+07f, 1.288308E+07f, 1.290063E+07f, 1.291818E+07f, 1.293573E+07f, 1.295328E+07f, 1.295328E+07f, 1.297084E+07f, 1.297084E+07f, 1.298839E+07f, 1.298839E+07f, 1.298839E+07f, 1.298839E+07f, 1.298839E+07f, 1.298839E+07f, 1.298839E+07f, 1.298839E+07f, 1.298839E+07f, 1.298839E+07f, 1.298839E+07f, 1.298839E+07f, 1.298839E+07f, 1.298839E+07f, 1.298839E+07f, 1.298839E+07f, 1.298839E+07f, 1.298839E+07f, 1.298839E+07f, 1.298839E+07f, 1.298839E+07f, 1.298839E+07f, 1.300594E+07f, 1.300594E+07f, 1.302349E+07f, 1.304104E+07f, 1.305859E+07f, 1.30937E+07f, 1.311125E+07f, 1.31288E+07f, 1.314635E+07f, 1.316391E+07f, 1.318146E+07f, 1.319901E+07f, 1.321656E+07f, 1.323411E+07f, 1.325167E+07f, 1.325167E+07f, 1.326922E+07f, 1.326922E+07f, 1.328677E+07f, 1.330432E+07f, 1.330432E+07f, 1.330432E+07f, 1.332187E+07f, 1.333943E+07f, 1.335698E+07f, 1.335698E+07f, 1.337453E+07f, 1.339208E+07f, 1.340963E+07f, 1.340963E+07f, 1.342718E+07f, 1.344474E+07f, 1.346229E+07f, 1.347984E+07f, 1.349739E+07f, 1.351494E+07f, 1.355005E+07f, 1.35676E+07f, 1.36027E+07f, 1.363781E+07f, 1.367291E+07f, 1.367291E+07f, 1.370801E+07f, 1.372557E+07f, 1.376067E+07f, 1.377822E+07f, 1.381333E+07f, 1.383088E+07f, 1.384843E+07f, 1.386598E+07f, 1.390109E+07f, 1.391864E+07f, 1.391864E+07f, 1.393619E+07f, 1.395374E+07f, 1.397129E+07f, 1.398884E+07f, 1.40064E+07f, 1.402395E+07f, 1.405905E+07f, 1.409416E+07f, 1.412926E+07f, 1.414681E+07f, 1.418191E+07f, 1.419947E+07f, 1.421702E+07f, 1.423457E+07f, 1.426967E+07f, 1.430478E+07f, 1.433988E+07f, 1.435743E+07f, 1.437499E+07f, 1.439254E+07f, 1.439254E+07f, 1.442764E+07f, 1.442764E+07f, 1.444519E+07f, 1.446274E+07f, 1.446274E+07f, 1.446274E+07f, 1.446274E+07f, 1.446274E+07f, 1.446274E+07f, 1.446274E+07f, 1.446274E+07f, 1.446274E+07f, 1.446274E+07f, 1.446274E+07f, 1.444519E+07f, 1.442764E+07f, 1.441009E+07f, 1.439254E+07f, 1.437499E+07f, 1.435743E+07f, 1.433988E+07f, 1.432233E+07f, 1.430478E+07f, 1.430478E+07f, 1.426967E+07f, 1.426967E+07f, 1.423457E+07f, 1.421702E+07f, 1.418191E+07f, 1.414681E+07f, 1.412926E+07f, 1.409416E+07f, 1.405905E+07f, 1.402395E+07f, 1.40064E+07f, 1.395374E+07f, 1.393619E+07f, 1.391864E+07f, 1.390109E+07f, 1.390109E+07f, 1.388353E+07f, 1.388353E+07f, 1.388353E+07f, 1.388353E+07f, 1.388353E+07f, 1.388353E+07f, 1.388353E+07f, 1.388353E+07f, 1.388353E+07f, 1.388353E+07f, 1.390109E+07f, 1.391864E+07f, 1.393619E+07f, 1.395374E+07f, 1.398884E+07f, 1.398884E+07f, 1.40064E+07f, 1.402395E+07f, 1.402395E+07f, 1.40415E+07f, 1.405905E+07f, 1.40766E+07f, 1.412926E+07f, 1.414681E+07f, 1.416436E+07f, 1.418191E+07f, 1.419947E+07f, 1.421702E+07f, 1.423457E+07f, 1.423457E+07f, 1.423457E+07f, 1.423457E+07f, 1.423457E+07f, 1.423457E+07f, 1.423457E+07f, 1.423457E+07f, 1.423457E+07f, 1.423457E+07f, 1.423457E+07f, 1.423457E+07f, 1.423457E+07f, 1.421702E+07f, 1.419947E+07f, 1.418191E+07f, 1.416436E+07f, 1.416436E+07f, 1.412926E+07f, 1.411171E+07f, 1.409416E+07f, 1.40766E+07f, 1.405905E+07f, 1.40415E+07f, 1.402395E+07f, 1.40064E+07f, 1.397129E+07f, 1.397129E+07f, 1.395374E+07f, 1.393619E+07f, 1.393619E+07f, 1.391864E+07f, 1.391864E+07f, 1.390109E+07f, 1.388353E+07f, 1.388353E+07f, 1.386598E+07f, 1.384843E+07f, 1.383088E+07f, 1.379577E+07f, 1.376067E+07f, 1.372557E+07f, 1.370801E+07f, 1.369046E+07f, 1.365536E+07f, 1.363781E+07f, 1.362026E+07f, 1.36027E+07f, 1.358515E+07f, 1.35676E+07f, 1.35325E+07f, 1.351494E+07f, 1.349739E+07f, 1.347984E+07f, 1.346229E+07f, 1.344474E+07f, 1.339208E+07f, 1.337453E+07f, 1.335698E+07f, 1.333943E+07f, 1.332187E+07f, 1.332187E+07f, 1.330432E+07f, 1.326922E+07f, 1.325167E+07f, 1.323411E+07f, 1.321656E+07f, 1.319901E+07f, 1.316391E+07f, 1.314635E+07f, 1.31288E+07f, 1.311125E+07f, 1.307615E+07f, 1.304104E+07f, 1.302349E+07f, 1.300594E+07f, 1.300594E+07f, 1.300594E+07f, 1.300594E+07f, 1.300594E+07f, 1.300594E+07f, 1.300594E+07f, 1.302349E+07f, 1.304104E+07f, 1.307615E+07f, 1.30937E+07f, 1.311125E+07f, 1.314635E+07f, 1.316391E+07f, 1.318146E+07f, 1.319901E+07f, 1.321656E+07f, 1.323411E+07f, 1.323411E+07f, 1.323411E+07f, 1.323411E+07f, 1.325167E+07f, 1.325167E+07f, 1.325167E+07f, 1.325167E+07f, 1.325167E+07f, 1.325167E+07f, 1.325167E+07f, 1.325167E+07f, 1.325167E+07f, 1.325167E+07f, 1.325167E+07f, 1.325167E+07f, 1.325167E+07f, 1.325167E+07f, 1.323411E+07f, 1.323411E+07f, 1.321656E+07f, 1.319901E+07f, 1.318146E+07f, 1.316391E+07f, 1.314635E+07f, 1.31288E+07f, 1.305859E+07f, 1.304104E+07f, 1.298839E+07f, 1.295328E+07f, 1.291818E+07f, 1.288308E+07f, 1.286552E+07f, 1.284797E+07f, 1.283042E+07f, 1.279532E+07f, 1.277776E+07f, 1.276021E+07f, 1.272511E+07f, 1.270756E+07f, 1.269001E+07f, 1.26549E+07f, 1.263735E+07f, 1.260225E+07f, 1.258469E+07f, 1.256714E+07f, 1.256714E+07f, 1.254959E+07f, 1.253204E+07f, 1.253204E+07f, 1.253204E+07f, 1.251449E+07f, 1.251449E+07f, 1.251449E+07f, 1.251449E+07f, 1.251449E+07f, 1.249694E+07f, 1.249694E+07f, 1.249694E+07f, 1.249694E+07f, 1.247938E+07f, 1.247938E+07f, 1.246183E+07f, 1.244428E+07f, 1.240918E+07f, 1.239162E+07f, 1.235652E+07f, 1.233897E+07f, 1.230386E+07f, 1.226876E+07f, 1.225121E+07f, 1.221611E+07f, 1.219855E+07f, 1.219855E+07f, 1.2181E+07f, 1.216345E+07f, 1.216345E+07f, 1.21459E+07f, 1.21459E+07f, 1.212835E+07f, 1.212835E+07f, 1.212835E+07f, 1.212835E+07f, 1.212835E+07f, 1.211079E+07f, 1.211079E+07f, 1.211079E+07f, 1.211079E+07f, 1.211079E+07f, 1.211079E+07f, 1.211079E+07f, 1.211079E+07f, 1.211079E+07f, 1.211079E+07f, 1.211079E+07f, 1.211079E+07f, 1.211079E+07f, 1.211079E+07f, 1.211079E+07f, 1.211079E+07f, 1.211079E+07f, 1.211079E+07f, 1.211079E+07f, 1.209324E+07f, 1.207569E+07f, 1.207569E+07f, 1.204059E+07f, 1.202303E+07f, 1.200548E+07f, 1.198793E+07f, 1.197038E+07f, 1.195283E+07f, 1.193528E+07f, 1.191772E+07f, 1.190017E+07f, 1.188262E+07f, 1.186507E+07f, 1.181241E+07f, 1.181241E+07f, 1.179486E+07f, 1.177731E+07f, 1.177731E+07f, 1.177731E+07f, 1.175976E+07f, 1.175976E+07f, 1.17422E+07f, 1.17422E+07f, 1.17422E+07f, 1.17422E+07f, 1.17422E+07f, 1.17422E+07f, 1.172465E+07f, 1.172465E+07f, 1.172465E+07f, 1.172465E+07f, 1.172465E+07f, 1.172465E+07f, 1.172465E+07f, 1.172465E+07f, 1.172465E+07f, 1.172465E+07f, 1.17071E+07f, 1.168955E+07f, 1.1672E+07f, 1.163689E+07f, 1.161934E+07f, 1.160179E+07f, 1.156669E+07f, 1.154913E+07f, 1.151403E+07f, 1.149648E+07f, 1.147893E+07f, 1.146137E+07f, 1.144382E+07f, 1.144382E+07f, 1.139117E+07f, 1.139117E+07f, 1.137361E+07f, 1.137361E+07f, 1.137361E+07f, 1.137361E+07f, 1.137361E+07f, 1.137361E+07f, 1.135606E+07f, 1.135606E+07f, 1.135606E+07f, 1.135606E+07f, 1.135606E+07f, 1.135606E+07f, 1.135606E+07f, 1.135606E+07f, 1.135606E+07f, 1.135606E+07f, 1.133851E+07f, 1.133851E+07f, 1.133851E+07f, 1.133851E+07f, 1.133851E+07f, 1.130341E+07f, 1.130341E+07f, 1.128586E+07f, 1.12683E+07f, 1.125075E+07f, 1.121565E+07f, 1.116299E+07f, 1.112789E+07f, 1.107523E+07f, 1.105768E+07f, 1.102258E+07f, 1.098747E+07f, 1.095237E+07f, 1.091727E+07f, 1.089971E+07f, 1.088216E+07f, 1.086461E+07f, 1.082951E+07f, 1.081196E+07f, 1.081196E+07f, 1.07944E+07f, 1.07944E+07f, 1.077685E+07f, 1.07593E+07f, 1.07593E+07f, 1.074175E+07f, 1.074175E+07f, 1.074175E+07f, 1.074175E+07f, 1.074175E+07f, 1.074175E+07f, 1.074175E+07f, 1.074175E+07f, 1.074175E+07f, 1.07593E+07f, 1.07593E+07f, 1.077685E+07f, 1.07944E+07f, 1.07944E+07f, 1.081196E+07f, 1.082951E+07f, 1.082951E+07f, 1.086461E+07f, 1.088216E+07f, 1.089971E+07f, 1.089971E+07f, 1.091727E+07f, 1.091727E+07f, 1.091727E+07f, 1.091727E+07f, 1.091727E+07f, 1.091727E+07f, 1.089971E+07f, 1.088216E+07f, 1.082951E+07f, 1.07944E+07f, 1.07593E+07f, 1.070664E+07f, 1.068909E+07f, 1.067154E+07f, 1.065399E+07f, 1.063644E+07f, 1.061888E+07f, 1.060133E+07f, 1.058378E+07f, 1.056623E+07f, 1.054868E+07f, 1.051357E+07f, 1.049602E+07f, 1.047847E+07f, 1.046092E+07f, 1.042581E+07f, 1.039071E+07f, 1.030295E+07f, 1.026785E+07f, 1.023274E+07f, 1.019764E+07f, 1.018009E+07f, 1.016254E+07f, 1.014498E+07f, 1.010988E+07f, 1.009233E+07f, 1.007478E+07f, 1.005722E+07f, 1.003967E+07f, 1.002212E+07f, 9969464f, 9916809f, 9881705f, 9864154f, 9846602f, 9829050f, 9811497f, 9793945f, 9776394f, 9741290f, 9723738f, 9688635f, 9653531f, 9653531f, 9618427f, 9618427f, 9600875f, 9600875f, 9600875f, 9583323f, 9565771f, 9565771f, 9530667f, 9530667f, 9530667f, 9530667f, 9530667f, 9530667f, 9530667f, 9530667f, 9548219f, 9565771f, 9583323f, 9618427f, 9653531f, 9671083f, 9688635f, 9706186f, 9741290f, 9758842f, 9811497f, 9829050f, 9864154f, 9881705f, 9916809f, 9934361f, 9951913f, 9987016f, 1.000457E+07f, 1.003967E+07f, 1.005722E+07f, 1.007478E+07f, 1.010988E+07f, 1.014498E+07f, 1.016254E+07f, 1.016254E+07f, 1.018009E+07f, 1.019764E+07f, 1.021519E+07f, 1.023274E+07f, 1.023274E+07f, 1.023274E+07f, 1.023274E+07f, 1.023274E+07f, 1.023274E+07f, 1.023274E+07f, 1.023274E+07f, 1.021519E+07f, 1.019764E+07f, 1.016254E+07f, 1.014498E+07f, 1.012743E+07f, 1.009233E+07f, 1.003967E+07f, 1.000457E+07f, 9951913f, 9934361f, 9899257f, 9881705f, 9864154f, 9846602f, 9829050f, 9793945f, 9758842f, 9723738f, 9688635f, 9653531f, 9635979f, 9618427f, 9583323f, 9565771f, 9530667f, 9513116f, 9495564f, 9478012f, 9460460f, 9460460f, 9442908f, 9425357f, 9425357f, 9407805f, 9390253f, 9390253f, 9372701f, 9372701f, 9372701f, 9372701f, 9372701f, 9372701f, 9372701f, 9372701f, 9372701f, 9372701f, 9372701f, 9372701f, 9390253f, 9407805f, 9425357f, 9460460f, 9495564f, 9513116f, 9583323f, 9600875f, 9635979f, 9653531f, 9688635f, 9706186f, 9723738f, 9758842f, 9793945f, 9811497f, 9846602f};
float[] yValues = { 7286825f, 7286825f, 7269351f, 7269351f, 7269351f, 7269351f, 7251876f, 7251876f, 7234401f, 7234401f, 7234401f, 7234401f, 7234401f, 7234401f, 7234401f, 7234401f, 7234401f, 7234401f, 7234401f, 7234401f, 7234401f, 7216927f, 7199453f, 7181979f, 7181979f, 7164504f, 7164504f, 7147029f, 7129555f, 7112081f, 7077132f, 7042183f, 7024709f, 7007235f, 6972285f, 6954811f, 6937337f, 6919863f, 6902388f, 6884913f, 6867439f, 6867439f, 6832491f, 6815016f, 6797541f, 6780067f, 6762593f, 6762593f, 6745119f, 6745119f, 6727644f, 6727644f, 6710169f, 6710169f, 6710169f, 6710169f, 6710169f, 6710169f, 6710169f, 6727644f, 6762593f, 6780067f, 6832491f, 6849965f, 6867439f, 6902388f, 6937337f, 6954811f, 6972285f, 6989760f, 7024709f, 7042183f, 7077132f, 7094607f, 7112081f, 7129555f, 7129555f, 7129555f, 7129555f, 7129555f, 7129555f, 7147029f, 7147029f, 7147029f, 7147029f, 7147029f, 7147029f, 7147029f, 7147029f, 7147029f, 7147029f, 7147029f, 7147029f, 7147029f, 7129555f, 7112081f, 7077132f, 7059657f, 7007235f, 6972285f, 6954811f, 6937337f, 6902388f, 6867439f, 6832491f, 6815016f, 6797541f, 6780067f, 6710169f, 6710169f, 6692695f, 6675221f, 6640272f, 6622797f, 6605323f, 6587849f, 6570375f, 6535425f, 6517951f, 6500477f, 6483003f, 6465528f, 6448053f, 6448053f, 6430579f, 6430579f, 6413105f, 6413105f, 6413105f, 6413105f, 6413105f, 6413105f, 6413105f, 6413105f, 6413105f, 6413105f, 6413105f, 6413105f, 6413105f, 6413105f, 6430579f, 6448053f, 6483003f, 6500477f, 6552900f, 6570375f, 6622797f, 6640272f, 6657747f, 6675221f, 6692695f, 6710169f, 6745119f, 6762593f, 6780067f, 6797541f, 6849965f, 6867439f, 6902388f, 6954811f, 6972285f, 6989760f, 7007235f, 7042183f, 7059657f, 7059657f, 7059657f, 7059657f, 7059657f, 7059657f, 7059657f, 7059657f, 7059657f, 7059657f, 7059657f, 7059657f, 7059657f, 7059657f, 7059657f, 7059657f, 7042183f, 7042183f, 7024709f, 7007235f, 6989760f, 6989760f, 6972285f, 6954811f, 6937337f, 6919863f, 6902388f, 6867439f, 6832491f, 6815016f, 6797541f, 6780067f, 6762593f, 6745119f, 6727644f, 6710169f, 6692695f, 6675221f, 6657747f, 6657747f, 6640272f, 6622797f, 6622797f, 6622797f, 6622797f, 6622797f, 6622797f, 6622797f, 6622797f, 6622797f, 6622797f, 6640272f, 6657747f, 6692695f, 6692695f, 6710169f, 6727644f, 6745119f, 6762593f, 6780067f, 6780067f, 6797541f, 6815016f, 6832491f, 6849965f, 6867439f, 6884913f, 6902388f, 6919863f, 6937337f, 6954811f, 6972285f, 6989760f, 7007235f, 7024709f, 7042183f, 7059657f, 7077132f, 7094607f, 7112081f, 7129555f, 7147029f, 7164504f, 7181979f, 7199453f, 7234401f, 7234401f, 7251876f, 7251876f, 7269351f, 7286825f, 7304299f, 7321773f, 7321773f, 7321773f, 7321773f, 7321773f, 7321773f, 7321773f, 7321773f, 7321773f, 7321773f, 7321773f, 7304299f, 7286825f, 7269351f, 7251876f, 7234401f, 7216927f, 7199453f, 7181979f, 7164504f, 7147029f, 7129555f, 7112081f, 7094607f, 7077132f, 7042183f, 7024709f, 7007235f, 6989760f, 6954811f, 6937337f, 6919863f, 6902388f, 6849965f, 6832491f, 6815016f, 6797541f, 6780067f, 6780067f, 6762593f, 6762593f, 6762593f, 6745119f, 6745119f, 6745119f, 6745119f, 6745119f, 6745119f, 6762593f, 6762593f, 6797541f, 6832491f, 6867439f, 6884913f, 6884913f, 6919863f, 6954811f, 6954811f, 6972285f, 6989760f, 7007235f, 7042183f, 7042183f, 7059657f, 7077132f, 7094607f, 7094607f, 7112081f, 7112081f, 7112081f, 7112081f, 7112081f, 7112081f, 7112081f, 7112081f, 7112081f, 7112081f, 7112081f, 7094607f, 7077132f, 7042183f, 7024709f, 7024709f, 7007235f, 6989760f, 6989760f, 6972285f, 6954811f, 6937337f, 6937337f, 6919863f, 6902388f, 6902388f, 6902388f, 6902388f, 6902388f, 6902388f, 6902388f, 6902388f, 6902388f, 6902388f, 6902388f, 6902388f, 6902388f, 6902388f, 6902388f, 6919863f, 6919863f, 6954811f, 6972285f, 6972285f, 6989760f, 7024709f, 7042183f, 7059657f, 7094607f, 7112081f, 7129555f, 7164504f, 7181979f, 7199453f, 7234401f, 7251876f, 7269351f, 7286825f, 7321773f, 7321773f, 7339248f, 7339248f, 7356723f, 7374197f, 7374197f, 7374197f, 7374197f, 7374197f, 7391671f, 7391671f, 7409145f, 7409145f, 7426620f, 7426620f, 7426620f, 7444095f, 7444095f, 7461569f, 7479043f, 7496517f, 7513992f, 7513992f, 7513992f, 7531467f, 7548941f, 7548941f, 7566415f, 7601364f, 7618839f, 7636313f, 7653787f, 7671261f, 7688736f, 7706211f, 7741159f, 7793583f, 7828531f, 7846005f, 7880955f, 7880955f, 7898429f, 7898429f, 7915903f, 7933377f, 7933377f, 7950852f, 7950852f, 7950852f, 7950852f, 7950852f, 7950852f, 7950852f, 7968327f, 7985801f, 8003275f, 8020749f, 8038224f, 8055699f, 8073173f, 8090647f, 8108121f, 8125596f, 8160545f, 8178019f, 8195493f, 8212968f, 8212968f, 8230443f, 8247917f, 8265391f, 8282865f, 8282865f, 8282865f, 8282865f, 8282865f, 8282865f, 8282865f, 8282865f, 8265391f, 8230443f, 8212968f, 8195493f, 8178019f, 8160545f, 8160545f, 8143071f, 8143071f, 8125596f, 8108121f, 8108121f, 8090647f, 8090647f, 8073173f, 8038224f, 8038224f, 8020749f, 8020749f, 8003275f, 7985801f, 7985801f, 7968327f, 7950852f, 7950852f, 7933377f, 7933377f, 7933377f, 7933377f, 7915903f, 7898429f, 7898429f, 7898429f, 7898429f, 7898429f, 7898429f, 7880955f, 7880955f, 7880955f, 7880955f, 7880955f, 7880955f, 7880955f, 7880955f, 7880955f, 7880955f, 7880955f, 7898429f, 7898429f, 7933377f, 7968327f, 7985801f, 8003275f, 8020749f, 8055699f, 8073173f, 8108121f, 8108121f, 8143071f, 8178019f, 8178019f, 8212968f, 8212968f, 8230443f, 8247917f, 8265391f, 8282865f, 8282865f, 8317815f, 8335289f, 8352763f, 8387712f, 8405186f, 8422661f, 8440134f, 8457609f, 8475084f, 8510033f, 8527506f, 8544981f, 8562456f, 8614878f, 8632353f, 8667302f, 8684777f, 8737200f, 8772149f, 8789622f, 8824572f, 8842046f, 8859521f, 8876994f, 8894469f, 8929418f, 8929418f, 8946893f, 8946893f, 8946893f, 8946893f, 8946893f, 8946893f, 8946893f, 8946893f, 8946893f, 8946893f, 8911944f, 8894469f, 8859521f, 8824572f, 8789622f, 8772149f, 8702250f, 8684777f, 8667302f, 8632353f, 8614878f, 8597405f, 8562456f, 8544981f, 8510033f, 8492558f, 8475084f, 8457609f, 8440134f, 8422661f, 8405186f, 8387712f, 8370237f, 8352763f, 8352763f, 8352763f, 8352763f, 8352763f, 8352763f, 8352763f, 8352763f, 8352763f, 8352763f, 8370237f, 8370237f, 8387712f, 8387712f, 8405186f, 8422661f, 8422661f, 8440134f, 8457609f, 8492558f, 8527506f, 8544981f, 8562456f, 8579930f, 8597405f, 8614878f, 8632353f, 8649828f, 8667302f, 8702250f, 8719725f, 8737200f, 8772149f, 8789622f, 8807097f, 8824572f, 8842046f, 8876994f, 8894469f, 8911944f, 8929418f, 8946893f, 8964366f, 8964366f, 8981841f, 8999316f, 9016790f, 9034265f, 9034265f, 9051738f, 9051738f, 9051738f, 9051738f, 9051738f, 9051738f, 9051738f, 9016790f, 8999316f, 8964366f, 8946893f, 8929418f, 8911944f, 8876994f, 8859521f, 8842046f, 8824572f, 8807097f, 8789622f, 8772149f, 8754674f, 8702250f, 8667302f, 8649828f, 8632353f, 8614878f, 8597405f, 8579930f, 8562456f, 8544981f, 8510033f, 8492558f, 8492558f, 8492558f, 8492558f, 8492558f, 8492558f, 8492558f, 8492558f, 8492558f, 8492558f, 8492558f, 8492558f, 8510033f, 8544981f, 8544981f, 8562456f, 8562456f, 8597405f, 8614878f, 8632353f, 8667302f, 8702250f, 8719725f, 8754674f, 8789622f, 8824572f, 8842046f, 8859521f, 8876994f, 8911944f, 8929418f, 8964366f, 8964366f, 8999316f, 9016790f, 9034265f, 9086688f, 9104162f, 9139110f, 9156585f, 9174060f, 9209009f, 9243957f, 9261432f, 9261432f, 9261432f, 9261432f, 9261432f, 9261432f, 9261432f, 9261432f, 9261432f, 9261432f, 9261432f, 9243957f, 9226482f, 9191534f, 9174060f, 9156585f, 9086688f, 9051738f, 9034265f, 8999316f, 8981841f, 8964366f, 8929418f, 8894469f, 8876994f, 8842046f, 8824572f, 8807097f, 8789622f, 8772149f, 8754674f, 8702250f, 8684777f, 8667302f, 8667302f, 8649828f, 8614878f, 8597405f, 8579930f, 8562456f, 8562456f, 8527506f, 8510033f, 8492558f, 8475084f, 8440134f, 8422661f, 8422661f, 8387712f, 8370237f, 8370237f, 8370237f, 8370237f, 8370237f, 8335289f, 8335289f, 8335289f, 8335289f, 8335289f, 8335289f, 8335289f, 8335289f, 8335289f, 8335289f, 8335289f, 8352763f, 8370237f, 8405186f, 8440134f, 8457609f, 8492558f, 8510033f, 8527506f, 8562456f, 8579930f, 8597405f, 8597405f, 8632353f, 8632353f, 8667302f, 8702250f, 8719725f, 8754674f, 8754674f, 8754674f, 8754674f, 8754674f, 8754674f, 8754674f, 8754674f, 8737200f, 8719725f, 8702250f, 8684777f, 8667302f, 8649828f, 8632353f, 8614878f, 8562456f, 8527506f, 8440134f, 8422661f, 8387712f, 8352763f, 8317815f, 8300340f, 8282865f, 8265391f, 8247917f, 8212968f, 8212968f, 8160545f, 8143071f, 8125596f, 8108121f, 8108121f, 8090647f, 8090647f, 8073173f, 8073173f, 8055699f, 8055699f, 8055699f, 8038224f, 8038224f, 8038224f, 8038224f, 8038224f, 8020749f, 8020749f, 8003275f, 8003275f, 7985801f, 7950852f, 7933377f, 7915903f, 7915903f, 7880955f, 7863480f, 7846005f, 7828531f, 7793583f, 7776108f, 7758633f, 7741159f, 7723685f, 7706211f, 7706211f, 7706211f, 7706211f, 7706211f, 7706211f, 7706211f, 7706211f, 7706211f, 7706211f, 7706211f, 7706211f, 7723685f, 7723685f, 7741159f, 7741159f, 7741159f, 7741159f, 7741159f, 7741159f, 7741159f, 7741159f, 7741159f, 7741159f, 7741159f, 7741159f, 7741159f, 7741159f, 7741159f, 7741159f, 7723685f, 7723685f, 7688736f, 7671261f, 7653787f, 7583889f, 7566415f, 7513992f, 7461569f, 7444095f, 7409145f, 7374197f, 7356723f, 7321773f, 7304299f, 7286825f, 7269351f, 7251876f, 7234401f, 7199453f, 7181979f, 7164504f, 7164504f, 7164504f, 7164504f, 7164504f, 7164504f, 7164504f, 7164504f, 7164504f, 7164504f, 7164504f, 7164504f, 7164504f, 7181979f, 7199453f };
PointF[] points = xValues.Zip(yValues, (x, y) => new PointF(x, y)).ToArray();
// Create a region with the original values
GraphicsPath pathWithOriginalPoints = new GraphicsPath();
pathWithOriginalPoints.AddPolygon(points);
Region regionFromOriginalPoints = new Region(pathWithOriginalPoints);
// Create a region with the values divided by 1000
GraphicsPath pathDividedBy1000 = new GraphicsPath();
pathDividedBy1000.AddPolygon(points.Select(p => new PointF(p.X/1000f, p.Y/1000f)).ToArray());
Region regionDividedby1000 = new Region(pathDividedBy1000);
// Time call to Region.IsVisible(PointF)
var stopwatch = Stopwatch.StartNew();
Console.WriteLine("Computing region.IsVisible for points divided by 1000:");
regionDividedby1000.IsVisible(new PointF(0f, 0f));
var dividedBy1000Timing = stopwatch.ElapsedMilliseconds;
Console.WriteLine($"Elapsed time: {dividedBy1000Timing} ms");
stopwatch.Restart();
Console.WriteLine("Computing region.IsVisible for original points");
regionFromOriginalPoints.IsVisible(new PointF(0f, 0f));
var originalTiming = stopwatch.ElapsedMilliseconds;
Console.WriteLine($"Elapsed time: {originalTiming} ms");
}
}
}
2 ответа
транслятор
Время, необходимое, чтобы сделать один Region.IsVisible(Point) колл не зависит от количества баллов вообще. Вместо этого это зависит от количества прямоугольников, необходимых для полного и точного покрытия региона. Который зависит от..:
- формы, которые описывают эти точки и обычно
- размер формы.
Пример 1: прямоугольная область имеет четыре точки, и для ее покрытия всегда требуется один прямоугольник. Это не изменится, если вы добавите большое количество точек, если они все лежат по бокам прямоугольника!
Пример 2: Круглая область также (!) Имеет четыре точки (), но количество прямоугольников, необходимое для ее полного охвата **, зависит от диаметра этого круга. Смотрите графику внизу!
Полный рассказ
Region это не то, что я бы назвал "хорошо документированным" классом.
Вы можете видеть, что внутренняя работа, кажется, полагается на RegionData, который может получить доступ по телефону var RData = your Region.GetRegionData(),
Здесь то же самое: не очень хорошо задокументировано, если не сказать больше. Может быть, я просто не могу найти его, но, похоже, нет информации о том, как эти байты структурированы..
(Числа ниже предполагают, что каждая необходимая точка занимает 1 байт в качестве индикатора типа плюс 2+4 байта для двух координат с плавающей точкой. Это было бы похоже на PathPoints&PathTypes в GraphicsPath , В вашем примере с 924+1 баллами и 1+2*4 байтами это составляет 8325 байтов; есть еще 27 байтов; 8 мог держать масштабирование..)
Интересно, однако, одно: RegionData от обоих ваших Regions легко увидеть, что они имеют одинаковый размер.. 8352, Это признак того, что RegionData не имеют прямого отношения к дополнительному времени в любом случае..
Но есть еще одно, не менее загадочное, чтение: плохо документированный вызов: GetRegionScans, MSDN говорит об этом:
Возвращает массив структур RectangleF, которые аппроксимируют эту область после применения указанного преобразования матрицы.
Сначала давайте посмотрим, что произойдет, если мы вытащим эти "сканы" для обоих ваших регионов:
Matrix M = new Matrix();
var scans1 = regionFromOriginalPoints.GetRegionScans(M);
var scans2 = regionDividedby1000.GetRegionScans(M);
Я использую простую единичную матрицу (*), то есть без преобразования, и вот результаты:
scans1.Length = 5.960.690
scans2.Length = 5.956
Таким образом, он создает в 1000 раз больше прямоугольников, чтобы приблизить Region и, о чудо, для этого тоже требуется много времени..
В этом нет ничего удивительного: немасштабированный путь охватывает огромную площадь, и для ее приближения я бы ожидал, что понадобится еще много прямоугольников. Я не знаю, как работает приближение, но это может решить, хотя RectangleF возвращаются, прямоугольник с любой стороной менее 1 пикселя не требуется.
Итак, я заключаю, что IsVisible вызов внутренне должен создать эти аппроксимативные прямоугольники, и ему нужно их достаточно, чтобы покрыть каждый полный пиксель внутри области. (Обратите внимание, что Region не поддерживает частичные / сглаженные пиксели!) Чем больше границы области, тем больше пикселей вмещается и тем дольше длится процесс сканирования.
Я также предполагаю, что именно процесс сканирования съедает время.
Далее: делать RectangleF.Contains(Point) должно быть очень быстро, даже для миллиона звонков. Посмотрим; когда я измеряю это:
int hits = 0;
PointF pt = new PointF(123.456f, 789.012f);
foreach (RectangleF r in scans1) if (r.Contains(pt)) hits++;
..это только занимает 42ms завершить. Таким образом, после того как вы кэшировали прямоугольники сканирования, вы можете легко выполнить множество тестов на них вместо того, чтобы делать отдельные IsVisible звонки..
Вот краткое изложение чисел:
Ваш оригинальный путь:
количество точек многоугольника = 924
regionData1.Length = 8,352
scans1.Length = 5.960.690
Истекшее время1: 453,187 мсПуть уменьшен до 1000:
количество точек многоугольника = 924
regionData2.Length = 8,352
scans2.Length = 5.956
Истекшее время2: 2 мсИстекшее время для полного набора сканов: 41 мс
Наконец, чтобы лучше понять прямоугольники сканирования, я приблизил круг чередующимися цветами:
for (int i = 0; i < scans.Length; i++)
g.FillRectangle(i%2 == 0 ? Brushes.ForestGreen : Brushes.Salmon, scans[i]);
Вы можете видеть, что сверху и снизу каждой строки является один прямоугольник, потому что здесь кривая плоская, а координаты x быстро перемещаются наружу. Чем ближе мы подходим к середине, тем больше (т.е. выше) прямоугольников можно получить... Итак, мы видим, что аппроксимация строго следует за строками..
Это справедливо даже в том случае, если ограничивающий прямоугольник выше ширины и, используя столбцы, можно сделать меньше прямоугольников:
Здесь оба эллипса (222x111 а также 111x222) аппроксимируются 85 горизонтальные полосы. Это меньше, чем круг из-за разной кривизны..
(*) - Мы пропустили Matrix; но его можно использовать для изменения результата путем увеличения или уменьшения масштаба данных. Круг имеет Height из 222 пикселей и это занимает 135 сканировать прямоугольники, чтобы приблизить его. Если мы увеличим Matrix (то есть Graphics объект, используемый для представления Region): m.Scale(10,10); занимает 1315 отсканируйте прямоугольники, чтобы покрыть масштабированный круг.
Таким образом, матрица уменьшена на 0.001f может использоваться вместо масштабирования ваших точек данных; но он будет тестировать только уменьшенную версию и, скорее всего, пропустит пиксели вокруг границ или включит неправильные. Поэтому лучше использовать только ту шкалу, которая вам действительно нужна.
(* *) Обратите внимание, что циркуляр GraphicsPath имеет 13 PathPoints ; но на самом деле это всего лишь четыре действительные точки (плюс первая, повторенная для закрытия фигуры) плюс две контрольные точки между каждой парой точек; поэтому 5 + 4*2 = 13. Также обратите внимание, что любая строка в GraphicsPath либо прямая, либо кривая Безье. Это включает в себя дуги, эллипсы и круги!
Мы боролись с той же проблемой: с полигоном в 50 тысяч точек у нас уходит 45 секунд на построение прямоугольников за методом IsVisible(). Мы пытались кэшировать эти данные, но в итоге у нас было более 1 миллиона прямоугольников; с несколькими регионами у нас было сотни мегабайт данных для кэширования.
Наконец, мы перешли к алгоритму PNPoly, который занимает всего несколько мс:
https://wrf.ecse.rpi.edu/Research/Short_Notes/pnpoly.html
Вот версия C#:
public bool IsVisible(Point p, List<Point> points)
{
int i, j = points.Count - 1;
bool isVisible = false;
for (i = 0; i < points.Count; i++)
{
if (points[i].Y < p.Y && points[j].Y >= p.Y
|| points[j].Y < p.Y && points[i].Y >= p.Y)
{
if (points[i].X + (p.Y - points[i].Y) / (points[j].Y - points[i].Y)
* (points[j].X - points[i].X) < p.X)
{
isVisible = !isVisible;
}
}
j = i;
}
return isVisible;
}