Каково будет число достижимых состояний, если модельные состояния Petri-Net находятся в цикле
Если у меня есть модель сети Петри из 8 мест и 8 транзакций. В этой модели нет мертвых состояний, потому что токен находится в цикле и проходит все 8 мест в первом цикле. Во втором и оставшихся циклах он пройдет через 6 мест, потому что токен попадет в Place3 при выполнении T5. Здесь я хочу знать, каким будет число достижимых состояний. Достижимые состояния будут бесконечными (из-за цикла) или как? 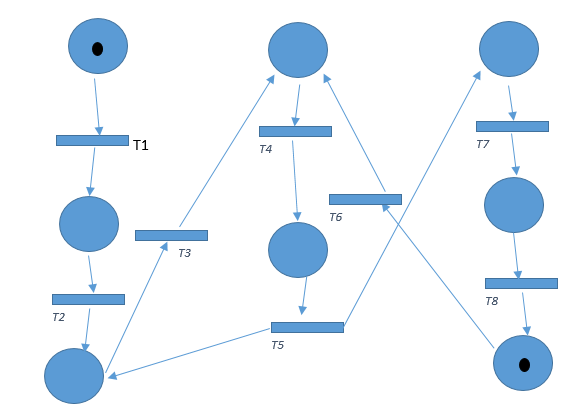
2 ответа
Немного сложно ответить, не видя точную сеть, но если предположить, что это простой цикл с одним токеном, то есть четыре состояния - различная маркировка мест с токенами - которые повторяются бесконечно.
Обновить
Ага! Это целый котелок рыбы. Olay, так что смоделируй это вручную. Я сделал это, положив один палец на каждый токен и следуя за ними. Я собираюсь назвать места от p_0 до P_7, взяв P_0 вверху слева и P_7 внизу справа, поэтому левый столбец - P_0, P_1, P_2, середина - P_3, P_4, правая P_5, P_6, P_7. Итак, мы начинаем с помеченных мест как {P_0,P_7}.
Начните:
{P_0, P_7}, T_1, T_6 огонь.
{P_1, P_3} и T_1,T_4 огонь.
{P_2, P_4} и T_2, T_5 стреляют и вот кикер:
{P_2, P_3, P_5} теперь у всех есть токены. Нет пути, который "съедает" токены, нет стоков, поэтому каждый раз, когда P_4 получает токен, T_5 срабатывает, и в P_5 появляется новый токен. T_5 будет включаться бесконечно часто, количество токенов будет увеличиваться как минимум на 1 каждый раз, поэтому набор достижимости бесконечен.
Это хорошая слайд-колода на сетях Петри. http://www.labri.fr/perso/anca/FDS/Pn-ESTII.pdf
Я думаю, что число "достижимых состояний" вашей сети бесконечно.
Я позволил себе создать интерактивную PDF-версию вашей диаграммы, чтобы вы могли "вручную" запускать переходы и видеть для себя вид меток, эволюционирующих от запуска разрешенных переходов.
Интерактивная версия сети Петри Усмана 1
Вот ссылка: https://www.academia.edu/34702296/An_Interactive_Version_of_Usmans_Petri_Net