Таблицы сопряженности в r2dtable слишком сконцентрированы
Я использую R's r2dtable функция для генерации таблиц сопряженности с заданными маргиналами. Однако при проверке итоговых таблиц значения выглядят слишком концентрированными по отношению к средним точкам. Пример:
set.seed(1)
matrices <- r2dtable(1e4, c(100, 100), c(100, 100))
vec.vals <- vapply(matrices, function(x) x[1, 1], numeric(1))
> table(vec.vals)
vec.vals
36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51
1 1 1 7 25 49 105 182 268 440 596 719 954 1072 1152 1048
52 53 54 55 56 57 58 59 60 61 62
1022 775 573 404 290 156 83 50 19 6 2
Таким образом, минимальное значение верхнего левого угла составляет 36, а максимальное - 62 из 10000 симуляций.
Есть ли способ получить несколько менее концентрированные матрицы?
2 ответа
Вы должны учитывать, что было бы крайне маловероятным, чтобы любое данное случайное ничье имело значение со значением и верхним левым углом 35. 1e4 попыток может быть недостаточно для реализации такого события. Посмотрите на теоретические предсказания (любезно предоставлено П. Далгаардом в список Релпа сегодня утром.):
round(dhyper(0:100,100,100,100)*1e4)
[1] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
[18] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
[35] 0 0 0 1 4 9 21 45 88 160 269 417 596 787 959 1081 1124
[52] 1081 959 787 596 417 269 160 88 45 21 9 4 1 0 0 0 0
[69] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
[86] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
Если вы увеличиваете число ничьих, вероятность одного значения 1 "увеличивается":
vec.vals <- vapply(matrices, function(x) x[1, 1], numeric(1)); table(vec.vals)
vec.vals
33 34 35 36 37 38 39 40 41 42 43 44 45
1 3 8 47 141 359 864 2148 4515 8946 15928 27013 41736
46 47 48 49 50 51 52 53 54 55 56 57 58
59558 78717 96153 108322 112524 107585 96042 78054 60019 41556 26848 16134 8627
59 60 61 62 63 64 65 66 68
4580 2092 933 351 138 42 11 4 1
... как и предполагалось:
round(dhyper(0:100,100,100,100)*1e6)
[1] 0 0 0 0 0 0 0 0 0 0 0 0
[13] 0 0 0 0 0 0 0 0 0 0 0 0
[25] 0 0 0 0 0 0 0 0 0 1 4 13
[37] 43 129 355 897 2087 4469 8819 16045 26927 41700 59614 78694
[49] 95943 108050 112416 108050 95943 78694 59614 41700 26927 16045 8819 4469
[61] 2087 897 355 129 43 13 4 1 0 0 0 0
[73] 0 0 0 0 0 0 0 0 0 0 0 0
[85] 0 0 0 0 0 0 0 0 0 0 0 0
[97] 0 0 0 0 0
Чтобы получить менее концентрированные матрицы, вам нужно найти баланс между количеством столбцов / строк, итогами и количеством матриц. Рассмотрим следующие наборы:
m2rep <- r2dtable(1e4, rep(100,2), rep(100,2))
m2seq <- r2dtable(1e4, seq(50,100,50), seq(50,100,50))
который дает различия в количестве уникальных значений:
> length(unique(unlist(m2rep)))
[1] 29
> length(unique(unlist(m2seq)))
[1] 58
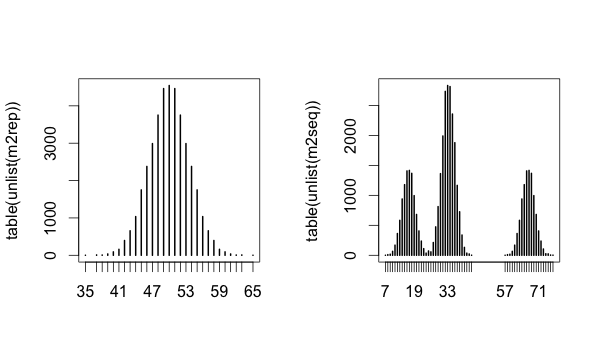
заговор это с:
par(mfrow = c(1,2))
plot(table(unlist(m2rep)))
plot(table(unlist(m2seq)))
дает:
Теперь рассмотрим:
m20rep <- r2dtable(1e4, rep(100,20), rep(100,20))
m20seq <- r2dtable(1e4, seq(50,1000,50), seq(50,1000,50))
который дает:
> length(unique(unlist(m20rep)))
[1] 20
> length(unique(unlist(m20seq)))
[1] 130
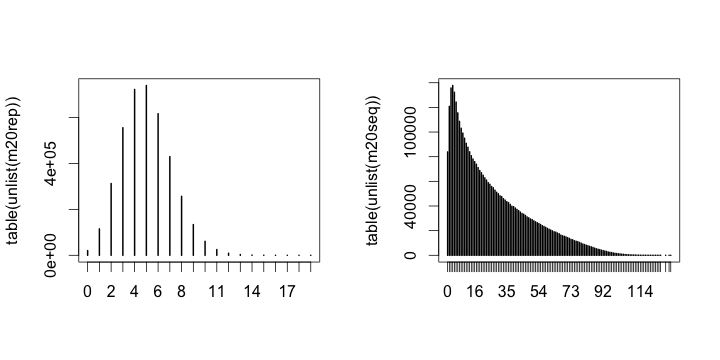
заговор это с:
par(mfrow = c(1,2))
plot(table(unlist(m20rep)))
plot(table(unlist(m20seq)))
дает:
Как видите, игра с параметрами помогает.
НТН