Наибольшее расстояние между множеством точек долготы / широты

Question

У меня есть набор координат lng/lat. Каким будет эффективный метод расчета наибольшего расстояния между любыми двумя точками в наборе ("максимальный диаметр", если хотите)?

Наивным способом является использование формулы Хаверсайна для вычисления расстояния между каждыми 2 точками и получения максимума, но это явно не масштабируется.

Изменить: точки расположены на достаточно маленькой области, измеряя область, в которой человек, несущий мобильное устройство, был активным в течение одного дня.

Answer 1

Я думаю, что следующее может быть полезным приближением, которое масштабируется линейно, а не квадратично с количеством точек, и это довольно легко реализовать:

1. рассчитать центр масс М из точек
2. найти точку P_0, которая имеет максимальное расстояние до M
3. найти точку P_1, которая имеет максимальное расстояние до P₀
4. приблизительный максимальный диаметр с расстоянием между P₀ и P₁

Это можно обобщить, повторив шаг 3 N раз и определив расстояние между P_N-1 и P_N

Шаг 1 может быть эффективно аппроксимирован М как среднее значение долготы и широты, что нормально, когда расстояния "малы", а полюса находятся достаточно далеко. Другие шаги могут быть выполнены с использованием формулы точного расстояния, но они намного быстрее, если координаты точек можно аппроксимировать как лежащие на плоскости. Как только "дальняя пара" (надеюсь, пара с максимальным расстоянием) найдена, ее расстояние можно пересчитать по точной формуле.

Примером приближения может быть следующее: если φ(M) и λ(M) - широта и долгота центра масс, рассчитанные как Σφ(P)/n и Σλ (P) / n,

• x (P) = (λ (P) - λ(M) + C) cos (φ (P))
• y (P) = φ (P) - φ(M) [это только для ясности, это также может быть просто y(P) = φ(P) ]

где C обычно 0, но может быть ± 360°, если набор точек пересекает линию λ=±180°. Чтобы найти максимальное расстояние, вы просто должны найти

• max ((x (P_N) - x (P_N-1))² + (y (P_N) - y (P_N-1))²)

(вам не нужен квадратный корень, потому что он монотонный)

Такое же преобразование координат можно использовать для повторения шага 1 (в новой системе координат), чтобы получить лучшую отправную точку. Я подозреваю, что если выполняются некоторые условия, описанные выше шаги (без повторения шага 3) всегда приводят к "истинной удаленной паре" (моя терминология). Если бы я только знал, какие условия...

РЕДАКТИРОВАТЬ:

Я ненавижу опираться на решения других, но кому-то придется.

Все еще сохраняя вышеуказанные 4 шага, с необязательным (но, вероятно, полезным, в зависимости от типичного распределения точек) повторением шага 3 и следуя решению Spacedman, выполнение вычислений в 3D преодолевает ограничения близости и расстояния от полюсов:

• x (P) = грех (φ (P))
• y (P) = cos (φ (P)) sin (λ (P))
• z (P) = cos (φ (P)) cos (λ (P))

(единственное приближение - это справедливо только для идеальной сферы)

Центр масс задается как x(M) = Σx(P)/n и т. Д., И максимум, который нужно искать, равен

• max ((x (P_N) - x (P_N-1))² + (y (P_N) - y (P_N-1))² + (z (P_N) - z (P_N-1))²)

Итак: сначала вы преобразуете сферические в декартовы координаты, затем начинаете с центра масс, чтобы найти, по крайней мере, в два шага (шаги 2 и 3) самую дальнюю точку от предыдущей точки. Вы можете повторять шаг 3 до тех пор, пока расстояние увеличивается, возможно, с максимальным количеством повторений, но это не отвлечет вас от локального максимума. Запуск из центра масс также не сильно поможет, если точки распределены по всей Земле.

РЕДАКТИРОВАТЬ 2:

Я выучил достаточно R, чтобы записать ядро ​​алгоритма (хороший язык для анализа данных!)

Для плоского приближения, игнорируя задачу вокруг линии λ=±180°:

# input: lng, lat (vectors)
rad = pi / 180;
x = (lng - mean(lng)) * cos(lat * rad)
y = (lat - mean(lat))
i = which.max((x - mean(x))^2 + (y       )^2)
j = which.max((x - x[i]   )^2 + (y - y[i])^2)
# output: i, j (indices)

На моем компьютере поиск индексов занимает менее секунды i а также j за 1000000 баллов.
Следующая 3D-версия немного медленнее, но работает для любого распределения точек (и не требует изменений при пересечении линии λ=±180°):

# input: lng, lat
rad = pi / 180
x = sin(lat * rad)
f = cos(lat * rad)
y = sin(lng * rad) * f
z = cos(lng * rad) * f
i = which.max((x - mean(x))^2 + (y - mean(y))^2 + (z - mean(z))^2)
j = which.max((x - x[i]   )^2 + (y - y[i]   )^2 + (z - z[i]   )^2)
k = which.max((x - x[j]   )^2 + (y - y[j]   )^2 + (z - z[j]   )^2) # optional
# output: j, k (or i, j)

Расчет k может быть опущен (т. е. результат может быть i а также j), в зависимости от данных и требований. С другой стороны, мои эксперименты показали, что вычисление дальнейшего индекса бесполезно.

Следует помнить, что в любом случае расстояние между результирующими точками является оценкой, которая является нижней границей "диаметра" набора, хотя очень часто это будет сам диаметр (как часто зависит от данных.)

РЕДАКТИРОВАТЬ 3:

К сожалению, относительная погрешность плоского приближения в крайних случаях может составлять 1-1/√3 ≅ 42,3%, что может быть неприемлемо, даже если очень редко. Алгоритм может быть изменен, чтобы иметь верхнюю границу приблизительно 20%, которую я получил по компасу и по прямой линии (аналитическое решение громоздко). Модифицированный алгоритм находит пару точек с локально максимальным расстоянием, затем повторяет те же шаги, но на этот раз, начиная со средней точки первой пары, возможно, находя другую пару:

# input: lng, lat
rad = pi / 180
x = (lng - mean(lng)) * cos(lat * rad)
y = (lat - mean(lat))
i.n_1 = 1 # n_1: n-1
x.n_1 = mean(x)
y.n_1 = 0 # = mean(y)
s.n_1 = 0 # s: square of distance
repeat {
   s = (x - x.n_1)^2 + (y - y.n_1)^2
   i.n = which.max(s)
   x.n = x[i.n]
   y.n = y[i.n]
   s.n = s[i.n]
   if (s.n <= s.n_1) break
   i.n_1 = i.n
   x.n_1 = x.n
   y.n_1 = y.n
   s.n_1 = s.n
}
i.m_1 = 1
x.m_1 = (x.n + x.n_1) / 2
y.m_1 = (y.n + y.n_1) / 2
s.m_1 = 0
m_ok  = TRUE
repeat {
   s = (x - x.m_1)^2 + (y - y.m_1)^2
   i.m = which.max(s)
   if (i.m == i.n || i.m == i.n_1) { m_ok = FALSE; break }
   x.m = x[i.m]
   y.m = y[i.m]
   s.m = s[i.m]
   if (s.m <= s.m_1) break
   i.m_1 = i.m
   x.m_1 = x.m
   y.m_1 = y.m
   s.m_1 = s.m
}
if (m_ok && s.m > s.n) {
   i = i.m
   j = i.m_1
} else {
   i = i.n
   j = i.n_1
}
# output: i, j

Трехмерный алгоритм может быть изменен аналогичным образом. Можно (как в 2D, так и в 3D) начать еще раз с середины второй пары точек (если она найдена). Верхняя граница в этом случае "оставлена ​​как упражнение для читателя":-).

Сравнение модифицированного алгоритма с (слишком) простым алгоритмом показало для нормального и для равномерного распределения квадратов почти удвоение времени обработки и уменьшение средней ошибки с 0,6% до 0,03% (порядок величины)., Дальнейший перезапуск со средней точки приводит к чуть лучшей средней ошибке, но почти равной максимальной ошибке.

РЕДАКТИРОВАТЬ 4:

Мне еще предстоит изучить эту статью, но похоже, что 20%, которые я нашел с помощью компаса и прямой линии, на самом деле 1-1/√(5-2√3) ≅ 19,3%

Answer 2

Теорема № 1: Порядок любых двух больших расстояний по кругу вдоль поверхности Земли такой же, как порядок по прямой линии между точками, где вы проходите через Землю.

Следовательно, превратите ваш широту в x,y,z на основе сферической земли произвольного радиуса или эллипсоида с заданными параметрами формы. Это пара синусов / косинусов на точку (не на пару точек).

Теперь у вас есть стандартная трехмерная задача, которая не зависит от вычисления расстояний Хаверсайна. Расстояние между точками просто евклидово (Пифагор в 3d). Нужен квадратный корень и несколько квадратов, и вы можете опустить квадратный корень, если вам нужны только сравнения.

Там могут быть причудливые структуры данных пространственного дерева, чтобы помочь с этим. Или такие алгоритмы, как http://www.tcs.fudan.edu.cn/rudolf/Courses/Algorithms/Alg_ss_07w/Webprojects/Qinbo_diameter/2d_alg.htm (нажмите "Далее" для 3d-методов). Или код C++ здесь: http://valis.cs.uiuc.edu/~sariel/papers/00/diameter/diam_prog.html

Как только вы нашли максимальную пару расстояний, вы можете использовать формулу Haversine, чтобы получить расстояние вдоль поверхности для этой пары.

Answer 3

Вы не говорите нам, будут ли эти точки расположены в достаточно маленькой части земного шара. Для действительно глобальных наборов точек мое первое предположение было бы запустить наивный алгоритм O(n^2), возможно, получив повышение производительности с помощью некоторой пространственной индексации (R*-деревья, восьмеричные деревья и т. Д.). Идея состоит в том, чтобы предварительно сгенерировать список n * (n-1) треугольника в матрице расстояний и передать его порциями в библиотеку быстрого расстояния, чтобы минимизировать ввод-вывод и обработать отток. Хаверсайн в порядке, вы также можете сделать это с помощью метода Винсенти (наибольший вклад во время выполнения - квадратичная сложность, а не (фиксированное число) итераций в формуле Винсенти). Как примечание, на самом деле вам не нужен R для этого материала.

РЕДАКТИРОВАТЬ #2: Алгоритм Barequet-Har-Peled(как указано Spacedman в его ответе) имеет сложность O((n+1/(e^3))log(1/e)) для e>0 и является стоит исследовать

Для квазиплоскостной задачи это известно как "диаметр выпуклой оболочки" и состоит из трех частей:

1. Вычисление выпуклой оболочки с помощью сканирования Грэма, которое является O (n * log (n)) - на самом деле, следует попытаться преобразовать точки в поперечную проекцию Меркатора (используя центр тяжести точек в наборе данных).
2. Нахождение антиподальных точек по алгоритму " Вращающиеся штангенциркули"- линейный O (n).
3. Нахождение наибольшего расстояния среди всех антиподальных пар - линейный поиск, O(n).

Ссылка с псевдокодом и обсуждение: http://fredfsh.com/2013/05/03/convex-hull-and-its-diameter/

См. Также обсуждение связанного вопроса здесь: https://gis.stackexchange.com/questions/17358/how-can-i-find-the-farthest-point-from-a-set-of-existing-points

РЕДАКТИРОВАТЬ: Решение Spacedman указал мне на алгоритм Malandain-Boissonnat(см. Статью в формате PDF здесь). Тем не менее, это хуже или так же, как алгоритм грубого наивного O(n^2).

Answer 4

Вот наивный пример, который не очень хорошо масштабируется (как вы говорите), как вы говорите, но может помочь в построении решения в R.

## lonlat points
n <- 100
d <- cbind(runif(n, -180, 180), runif(n, -90, 90))


library(sp)
## distances on WGS84 ellipsoid
x <- spDists(d, longlat = TRUE)

## row, then column index of furthest points
ind <- c(row(x)[which.max(x)], col(x)[which.max(x)])

## maps
library(maptools)
data(wrld_simpl)
plot(as(wrld_simpl, "SpatialLines"), col = "grey")

points(d, pch = 16, cex = 0.5)

## draw the points and a line between  on the page
points(d[ind, ], pch = 16)
lines(d[ind, ], lwd = 2)


## for extra credit, draw the great circle on which the furthest points lie
library(geosphere)


lines(greatCircle(d[ind[1], ], d[ind[2], ]), col = "firebrick")

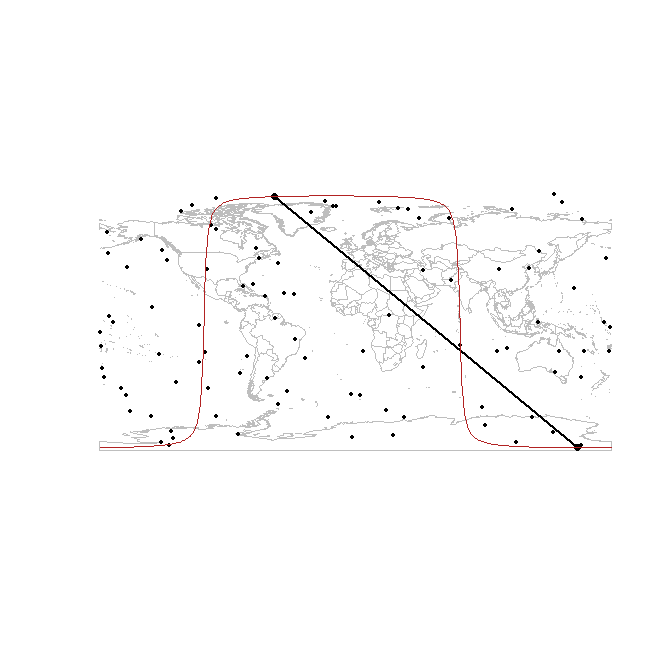
geosphere Пакет предоставляет больше возможностей для расчета расстояния, если это необходимо. Увидеть ?spDists в sp для деталей, используемых здесь.