Почему scipy.optimize.minimize (по умолчанию) сообщает об успехе, не переходя со Skyfield?

Question

scipy.optimize.minimize использование метода по умолчанию возвращает начальное значение в качестве результата, без каких-либо сообщений об ошибках или предупреждений. Хотя использование метода Nelder-Mead, предложенного в этом ответе, решает проблему, я хотел бы понять:

Почему метод по умолчанию возвращает неправильный ответ без предупреждения отправной точки в качестве ответа - и есть ли способ защитить меня от "неправильного ответа без предупреждения", чтобы избежать такого поведения в этом случае?

Обратите внимание, функция separation использует пакет Python Skyfield для генерации значений, которые должны быть минимизированы, что не гарантируется гладким, поэтому может быть именно поэтому Simplex лучше здесь.

РЕЗУЛЬТАТЫ:

результат теста: [ 2.14159739 ] "правильный": 2.14159265359 начальный: 0.0

результат по умолчанию: [ 10000. ] 'правильный': 13054 начальный: 10000

Результат Nelder -Mead: [ 13053.81011963 ] 'правильно': 13054, начальное: 10000

FULL OUTPUT using DEFAULT METHOD:
   status: 0
  success: True
     njev: 1
     nfev: 3
 hess_inv: array([[1]])
      fun: 1694.98753895812
        x: array([ 10000.])
  message: 'Optimization terminated successfully.'
      jac: array([ 0.])
      nit: 0

FULL OUTPUT using Nelder-Mead METHOD:
  status: 0
    nfev: 63
 success: True
     fun: 3.2179306044608054
       x: array([ 13053.81011963])
 message: 'Optimization terminated successfully.'
     nit: 28

Вот полный сценарий:

def g(x, a, b):
    return np.cos(a*x + b)

def separation(seconds, lat, lon):
    lat, lon, seconds = float(lat), float(lon), float(seconds) # necessary it seems
    place = earth.topos(lat, lon)
    jd = JulianDate(utc=(2016, 3, 9, 0, 0, seconds))
    mpos = place.at(jd).observe(moon).apparent().position.km
    spos = place.at(jd).observe(sun).apparent().position.km
    mlen = np.sqrt((mpos**2).sum())
    slen = np.sqrt((spos**2).sum())
    sepa = ((3600.*180./np.pi) *
            np.arccos(np.dot(mpos, spos)/(mlen*slen)))
    return sepa

from skyfield.api import load, now, JulianDate
import numpy as np
from scipy.optimize import minimize

data = load('de421.bsp')

sun   = data['sun']
earth = data['earth']
moon  = data['moon']

x_init = 0.0
out_g = minimize(g, x_init, args=(1, 1))
print "test result: ", out_g.x, "'correct': ", np.pi-1, "initial: ", x_init    # gives right answer

sec_init = 10000
out_s_def = minimize(separation, sec_init, args=(32.5, 215.1))
print "default result: ", out_s_def.x, "'correct': ", 13054, "initial: ", sec_init

sec_init = 10000
out_s_NM = minimize(separation, sec_init, args=(32.5, 215.1),
                 method = "Nelder-Mead")
print "Nelder-Mead result: ", out_s_NM.x, "'correct': ", 13054, "initial: ", sec_init

print ""
print "FULL OUTPUT using DEFAULT METHOD:"
print out_s_def
print ""
print "FULL OUTPUT using Nelder-Mead METHOD:"
print out_s_NM

Answer 1

1)

Ваша функция кусочно-постоянна (имеет мелкомасштабную "лестничную клетку"). Это не везде дифференцируемо.

Градиент функции при первоначальном предположении равен нулю.

Оптимизатор BFGS по умолчанию видит нулевой градиент и решает, что он является локальным минимумом по своим критериям (которые основаны на предположениях о входной функции, которые в этом случае не верны, например, дифференцируемость).

В основном, ровные области бомбят оптимизатор. Оптимизатор исследует функцию в небольшой ровной области вокруг начальной точки, где все выглядит так, будто функция является просто константой, поэтому думает, что вы дали ей постоянную функцию. Поскольку ваша функция не везде дифференцируема, возможно, что почти все начальные точки находятся внутри таких плоских областей, так что это может произойти без везения при выборе начальной точки.

Также обратите внимание, что Nelder-Mead не застрахован от этого - просто случается, что его начальный симплекс больше, чем размер лестницы, поэтому он исследует функцию вокруг большего места. Если начальный симплекс будет меньше, чем размер лестницы, оптимизатор будет вести себя так же, как BFGS.

2)

Общий ответ: локальные оптимизаторы возвращают локальные оптимумы. Совпадают ли они с истинным оптимумом, зависит от свойств функции.

В общем, чтобы увидеть, застряли ли вы в локальном оптимуме, попробуйте разные начальные догадки.

Кроме того, использование оптимизатора на основе производной для недифференцируемой функции не является хорошей идеей. Если функция дифференцируется в "большом" масштабе, вы можете отрегулировать размер шага численного дифференцирования.

Поскольку не существует дешевого / общего способа численной проверки, если функция везде дифференцируема, такая проверка не выполняется - вместо этого это предположение в методе оптимизации, которое должно быть обеспечено тем, кто вводит целевую функцию и выбирает метод оптимизации.,

Answer 2

Я не могу превозносить ценность print заявление о том, как алгоритм ведет себя во времени. Если вы попытаетесь добавить один в верхней части вашего separation() функция, то вы увидите, как подпрограммы минимизации работают в направлении ответа:

def separation(seconds, lat, lon):
    print seconds
    ...

Добавление этой строки позволит вам увидеть, что метод Nelder-Mead производит тщательный поиск диапазона секунд, шагая вперед с шагом в 500 секунд, прежде чем он начнет играть:

[ 10000.]
[ 10500.]
[ 11000.]
[ 11500.]
[ 12500.]
...

Конечно, он не знает, что это 500-секундные приращения, потому что для решения, подобного этому, проблема не имеет единиц измерения. Эти корректировки могут составлять 500 метров, или 500 ангстрем, или 500 лет. Но он спотыкается вслепую и, в случае с Nelder-Mead, видит достаточно того, как выходные данные меняются в зависимости от того, как вводить ответ, который вам нравится.

Здесь, для сравнения, весь поиск выполняется по умолчанию:

[ 10000.]
[ 10000.00000001]
[ 10000.]

Вот и все. Он пытается слегка отступить на 1e-8 секунд, не видит различий в ответе, который получает, и сдается - как правильно утверждали несколько других ответов.

Иногда вы можете исправить ситуацию, подобную этой, сказав алгоритму: (а) сделать больший шаг для начала и (б) прекратить тестирование, как только размер шага, который он делает, становится маленьким - скажем, когда он падает до миллисекунды. Вы можете попробовать что-то вроде:

out_s_def = minimize(separation, sec_init, args=(32.5, 215.1),
                     tol=1e-3, options={'eps': 500})

В этом случае все еще кажется, что техника минимизации по умолчанию является слишком хрупкой, чтобы конструктивно находить минимум, даже когда предоставляется эта помощь, поэтому мы можем сделать что-то еще: мы можем сказать функции минимизации, с каким количеством битов она действительно должна играть.

Видите ли, эти процедуры минимизации часто пишутся с довольно явным знанием того, насколько точной может быть вытолкнута 64-битная операция с плавающей запятой, прежде чем больше нет точности, и все они предназначены для остановки до этой точки. Но вы скрываете точность: вы говорите подпрограмме "дай мне количество секунд", которая заставляет их думать, что они могут играть даже с очень маленькими младшими цифрами значения секунд, когда на самом деле секунды объединяются с не только часы и дни, но и годы, и при этом любая крошечная точность внизу секунд теряется - хотя минимизатор не знает!

Итак, давайте выставим реальное время с плавающей запятой алгоритму. В процессе я сделаю три вещи:

1. Давайте избегать необходимости float() маневр вы делаете. наш print выражение показывает проблему: даже если вы предоставили скалярное число с плавающей точкой, минимизатор все равно превращает его в массив NumPy:

   (array([ 10000.]), 32.5, 215.1)
   

   Но это легко исправить: теперь, когда Skyfield имеет separation_from() встроенный, который может нормально обрабатывать массивы, мы будем использовать его:

   sepa = mpos.separation_from(spos)
   return sepa.degrees
   

2. Я переключусь на новый синтаксис для создания дат, который Скайфилд принял, поскольку он приближается к 1.0.

Это дает нам что-то вроде (но обратите внимание, что это будет быстрее, если вы только построили topos один раз и передал его, вместо того, чтобы перестраивать его и заставлять каждый раз делать свою математику):

ts = load.timescale()

...

def separation(tt_jd, lat, lon):
    place = earth.topos(lat, lon)
    t = ts.tt(jd=tt_jd)
    mpos = place.at(t).observe(moon).apparent()
    spos = place.at(t).observe(sun).apparent()
    return mpos.separation_from(spos).degrees

...

sec_init = 10000.0
jd_init = ts.utc(2016, 3, 9, 0, 0, sec_init).tt
out_s_def = minimize(separation, jd_init, args=(32.5, 215.1))

Результатом является успешное минирование, дающее - я думаю, вы могли бы перепроверить меня здесь? - ответ, который вы ищете:

print ts.tt(jd=out_s_def.x).utc_jpl()

['A.D. 2016-Mar-09 03:37:33.8224 UT']

Я надеюсь вскоре объединить несколько предварительно подготовленных подпрограмм минификации со Skyfield - на самом деле, серьезной причиной для написания этой программы вместо PyEphem было желание использовать мощные оптимизаторы SciPy и отказаться от довольно анемичных, которые PyEphem реализует в C. Главное, с чем они должны быть осторожны, это то, что произошло здесь: оптимизатору нужно дать цифры с плавающей запятой, чтобы они колебались, которые являются существенными на всем пути вниз.

Может быть, мне стоит посмотреть, как объекты Time могут составлять свое время из двух объектов с плавающей запятой, чтобы можно было представить намного больше секундных цифр. Я думаю, что AstroPy сделал это, и это традиционно в программировании астрономии.

Answer 3

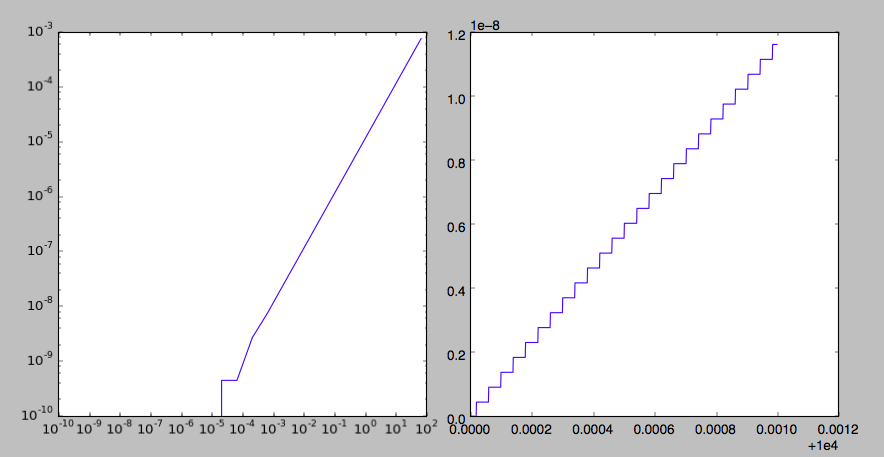
Принятый ответ от @pv. объясняет, что Skyfield имеет "лестничный" ответ, означающий, что некоторые значения, которые он возвращает, являются локально плоскими, за исключением дискретных переходов.

Я провел небольшой эксперимент на первом шаге - преобразовал время в объекты JulianDate, на самом деле это выглядит примерно как 40 микросекунд на приращение, или около 5E-10 дней. Это разумно, учитывая, что базы данных JPL охватывают тысячи лет. Хотя это, вероятно, хорошо для почти любого общего применения в астрономическом масштабе, на самом деле это не так гладко. Как указывает ответ - локальная плоскостность вызовет "успех" в некоторых (возможно, во многих) минимизаторах. Это ожидаемо и разумно и никоим образом не является провалом метода.

from skyfield.api import load, now, JulianDate
import numpy as np
import matplotlib.pyplot as plt

t  = 10000 + np.logspace(-10, 2, 25)        # logarithmic spacing
jd = JulianDate(utc=(2016, 3, 9, 0, 0, t))

dt  = t[1:] - t[:-1]
djd = jd.tt[1:] - jd.tt[:-1]

t  = 10000 + np.linspace(0, 0.001, 1001)        # linear spacing
jd = JulianDate(utc=(2016, 3, 9, 0, 0, t))

plt.figure()

plt.subplot(1,2,1)

plt.plot(dt, djd)
plt.xscale('log')
plt.yscale('log')

plt.subplot(1,2,2)

plt.plot(t, jd.tt-jd.tt[0])

plt.show()