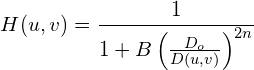High Pass Butterworth Фильтр по изображениям в MATLAB

Question

Мне нужно реализовать фильтр высоких частот Баттерворта в MATLAB для целей фильтрации изображений. Я реализовал один, но, похоже, он не работает. Вот код, который я написал. Может кто-нибудь сказать мне, что не так?

n=1;
d=50;
A=1.5;
im=imread('imagex.jpg');
h=size(im,1);
w=size(im,2);
[x y]=meshgrid(-floor(w/2):floor(w-1/2),-floor(h/2):floor(h-1/2));
hhp=(1./(d./(x.^2+y.^2).^0.5).^(2*n));
image_2Dfilter=fftshift(fft2(im));
Image_butterworth=image_2Dfilter;
imshow(Image_butterworth);
ifftshow(Image_butterworth);

Answer 1

Во-первых, нет такой команды под названием ifftshow, Во-вторых, вы ничего не фильтруете. Все, что вы делаете, это визуализируете спектр изображения.

С точки зрения визуализации спектра, то, как вы делаете это прямо сейчас, очень опасно. Во-первых, вы визуализируете коэффициенты для каждого компонента пространственной частоты, который имеет комплексную природу. Если вы хотите визуализировать спектр таким образом, который имеет смысл для большинства из нас, лучше взглянуть на величину или фазу. Однако, поскольку это фильтр Баттерворта, лучше всего применить его к величине фильтра.

Вы можете найти величину спектра, используя abs функция. Даже если вы делаете это, если вы сделали imshow непосредственно по величине вы получите визуализацию, которая равна нулю везде, кроме середины. Это связано с тем, что компонент постоянного тока настолько велик, а остальная часть спектра мала по сравнению.

Позвольте мне показать вам пример. Это изображение оператора, которое является частью набора инструментов для обработки изображений:

im = imread('cameraman.tif');
figure;
imshow(im);

Теперь давайте визуализируем спектр и убедимся, что компонент постоянного тока находится в центре изображения - вы уже сделали это с fftshift, Это также хорошая идея, чтобы бросить изображениеdouble чтобы обеспечить лучшую точность данных. Кроме того, убедитесь, что вы подаете заявку abs найти величину:

fftim = fftshift(fft2(double(im)));
mag = abs(fftim);
figure;
imshow(mag, []);

Как видите, это не очень полезно по той причине, о которой я упоминал. Лучшим способом визуализации спектра изображения обычно является применение лог- преобразования к спектру. Это также полезно, если вы хотите уменьшить или удалить среднее значение, чтобы динамический диапазон лучше подходил для отображения. Другими словами, вы должны добавить 1 к величине, а затем применить логарифм к величине, чтобы более высокие значения могли сузиться. Неважно, какую базу вы используете, поэтому я просто использую натуральный логарифм, который инкапсулируется log команда:

figure;
imshow(log(1 + mag), []);

Теперь это намного лучше. Теперь перейдем к вашему фильтрующему механизму. Ваш фильтр Баттерворта немного неправильный. meshgrid координат немного неверно. -1 операция, которая находится в конце интервала, должна выходить наружу:

[x y]=meshgrid(-floor(w/2):floor(w/2)-1,-floor(h/2):floor(h/2)-1);

Помните, что вы определяете симметричный интервал относительно центра изображения, и то, что у вас изначально было неверно. Я также хотел бы отметить, что это похоже на фильтр верхних частот, поэтому вывод должен выглядеть как обнаружение края. Кроме того, определение фильтра высоких частот Баттерворта неверно. Правильное определение фильтра в частотной области:

D(u,v) расстояние от центра изображения в частотной области, Do это расстояние отсечки в то время как B является управляющим масштабным коэффициентом, управляющим желаемым коэффициентом усиления на расстоянии отсечки. n это порядок фильтра. Do в вашем случае это d = 50, На практике, B = sqrt(2) - 1 так что на расстоянии отсечки Do, D(u,v) = 1 / sqrt(2) = 0.707, которая является частотой среза 3 дБ, в основном наблюдаемой в электронных схемах фильтров. Иногда вы увидите B устанавливается для 1 для простоты, но обычно это установить B = sqrt(2) - 1,

Тем не менее, ваш текущий код не выполняет никакой фильтрации. Для фильтрации в частотной области вы просто умножаете спектр изображения на спектр самого фильтра. Это эквивалентно свертке в пространственной области. Как только вы это сделаете, вы просто отмените fftshift что было выполнено на изображении, возьмите обратное БПФ и затем исключите любые мнимые компоненты, которые из-за числовой неточности. Кроме того, давайте приведем к uint8 чтобы убедиться, что мы уважаем исходный тип изображения.

Это можно сделать так:

%// Your code with meshgrid fix
n=1;
d=50;
h=size(im,1);
w=size(im,2);
fftim = fftshift(fft2(double(im)));
[x y]=meshgrid(-floor(w/2):floor(w/2)-1,-floor(h/2):floor(h/2)-1);
%hhp=(1./(d./(x.^2+y.^2).^0.5).^(2*n));

%%%%%%// New code
B = sqrt(2) - 1; %// Define B
D = sqrt(x.^2 + y.^2); %// Define distance to centre
hhp = 1 ./ (1 + B * ((d ./ D).^(2 * n)));
out_spec_centre = fftim .* hhp;

%// Uncentre spectrum
out_spec = ifftshift(out_spec_centre);

%// Inverse FFT, get real components, and cast
out = uint8(real(ifft2(out_spec)));

%// Show image
imshow(out);

Если вы хотите увидеть, как выглядит отфильтрованный спектр, просто сделайте это:

figure;
imshow(log(1 + abs(out_spec_centre)), []);

Мы получаем:

Это имеет смысл. Вы видите, что в середине спектра он немного темнее по сравнению с внешними краями спектра. Это связано с тем, что с помощью фильтра высоких частот Баттерворта вы усиливаете высокочастотные слагаемые, и он визуализируется как более высокая интенсивность.

Сейчас, out содержит ваше отфильтрованное изображение, и мы наконец получаем это:

Это выглядит как хороший результат! Тем не менее, наивно бросая изображение uint8 обрезает все отрицательные значения до 0, а любые положительные значения больше, чем от 255 до 255. Поскольку это обнаружение фронта, вы хотите обнаруживать как отрицательные, так и положительные переходы... поэтому хорошей идеей будет нормализовать выходной сигнал так, чтобы он находился в диапазоне от [0,1], а затем бросить с uint8 после умножения на 255. Таким образом, никакие изменения в изображении не будут отображаться серым, отрицательные изменения будут отображаться как темные, а положительные изменения будут отображаться в белом цвете.... так что вы должны сделать что-то вроде этого:

%// Your code with meshgrid fix
n=1;
d=50;
h=size(im,1);
w=size(im,2);
fftim = fftshift(fft2(double(im)));
[x y]=meshgrid(-floor(w/2):floor(w/2)-1,-floor(h/2):floor(h/2)-1);
%hhp=(1./(d./(x.^2+y.^2).^0.5).^(2*n));

%%%%%%// New code
B = sqrt(2) - 1; %// Define B
D = sqrt(x.^2 + y.^2); %// Define distance to centre
hhp = 1 ./ (1 + B * ((d ./ D).^(2 * n)));
out_spec_centre = fftim .* hhp;

%// Uncentre spectrum
out_spec = ifftshift(out_spec_centre);

%// Inverse FFT, get real components
out = real(ifft2(out_spec));

%// Normalize and cast
out = (out - min(out(:))) / (max(out(:)) - min(out(:)));
out = uint8(255*out);

%// Show image
imshow(out);

Мы получаем это:

Answer 2

Я думаю, что вы должны работать немного по-другому

n=1;
D0=50; % change the name for d0, d is usuaally the (u²+v²)⁽1/2)

A=1.5; % normally the amplitude is 1

im=imread('cameraman.jpg');

[M,N]=size(im); % is easy to get the h and w like this

% compute the 2d fourier transform in order to multiply

F=fft2(double(im));

% compute your filter and do the meshgrid for your matrix but it is M*n, and get only the real part

u=0:(M-1);
v=0:(N-1);

idx=find(u>M/2);
u(idx)=u(idx)-M;
idy=find(v>N/2);
v(idy)=v(idy)-N;
[V,U]=meshgrid(v,u);
D=sqrt(U.^2+V.^2);
H =A * (1./(1 + (D0./D).^(2*n)));

% multiply element by element

G=H.*F;
g=real(ifft2(double(G)));
subplot(1,2,1); imshow(im); title('Input image');
subplot(1,2,2); imshow(g,[ ]); title('filtered image');