Равномерная выборка в круге единицы

Question

Я хочу выбрать двухмерный вектор x из равномерного распределения с ∥x∥ ≤ 1. Я знаю, что могу выбрать из равномерного распределения как

numpy.random.uniform(0.0, 1.0, 2)

но как я могу убедиться, что ∥x∥ ≤ 1?

Answer 1

Это можно сделать путем рандомизации угла и длины и преобразования их в декартовы координаты:

import numpy as np

length = np.sqrt(np.random.uniform(0, 1))
angle = np.pi * np.random.uniform(0, 2)

x = length * np.cos(angle)
y = length * np.sin(angle)

Редактировать: iguarna комментарий о первоначальном ответе является правильным. Для того, чтобы нарисовать точку равномерно, length должен быть квадратный корень из нарисованного случайного числа. Ссылка на него может быть найдена здесь: Имитация равномерного распределения на диске. Например, это результат случайных результатов без квадратного корня: 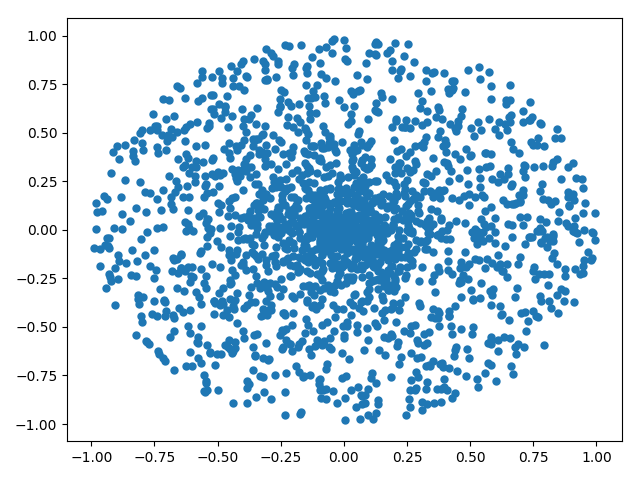И с квадратным корнем: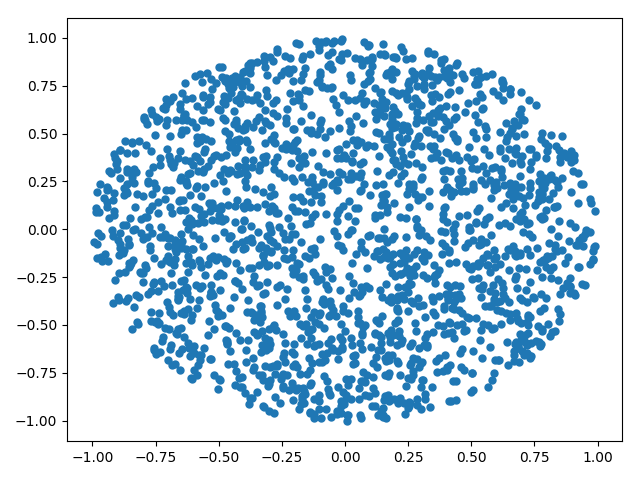

Answer 2

Выборка угла и длины, как указано выше, не гарантирует равномерную выборку из круга. В этом случае P (a)> P (b), если || a || > || b ||, Чтобы сделать выборку из круга, сделайте следующее:

length = np.random.uniform(0, 1)
angle = np.pi * np.random.uniform(0, 2)

x = np.sqrt(length) * np.cos(angle)
y = np.sqrt(length) * np.sin(angle)