Каково время выполнения моего алгоритма?

Question

Я пишу алгоритм, который сначала примет файл конфигурации с различными конечными точками и связанный с ними метод, как показано ниже:

/guest guestEndpoint
/guest/lists listEndpoint
/guest/friends guestFriendsEndpoint
/guest/X/friends guetFriendsEndpoint
/guest/X/friends/X guestFriendsEndpoint
/X/guest guestEndpoint
/X/lists listEndpoint
/options optionsEndpoint

X здесь представляет собой подстановочный знак, поэтому любая строка будет соответствовать этому. Алгоритм будет принимать это в качестве входных данных и строить дерево с каждым узлом, представляющим один токен между /"S. Каждый лист будет действительной конечной точкой.

Затем, когда пользователь переходит в нечто вроде guest/abc/friends это будет пересекать дерево, начиная с корня, а затем искать guest узел, прикрепленный к корню, если он существует, перейдите на узел guest, если guest здесь гость будет иметь wildcard узел, так что если abc не совпадает ни с одним из guestузлы, но там был wildcard присутствующий узел будет идти к wildcard, Тогда это будет выглядеть из wildcard чтобы увидеть, если это было friends узел, если так иди туда. Тогда если friendsэто листовой узел, он вернул бы соответствующий метод.

Имеет ли этот алгоритм смысл? Я задаюсь вопросом, каково время выполнения поиска. Я думаю, что это будет O(n), где n - количество токенов в параметре, который был передан.

Вот изображение графика, который я бы построил на основе приведенного выше ввода. Каждый ромб представляет метод конечной точки.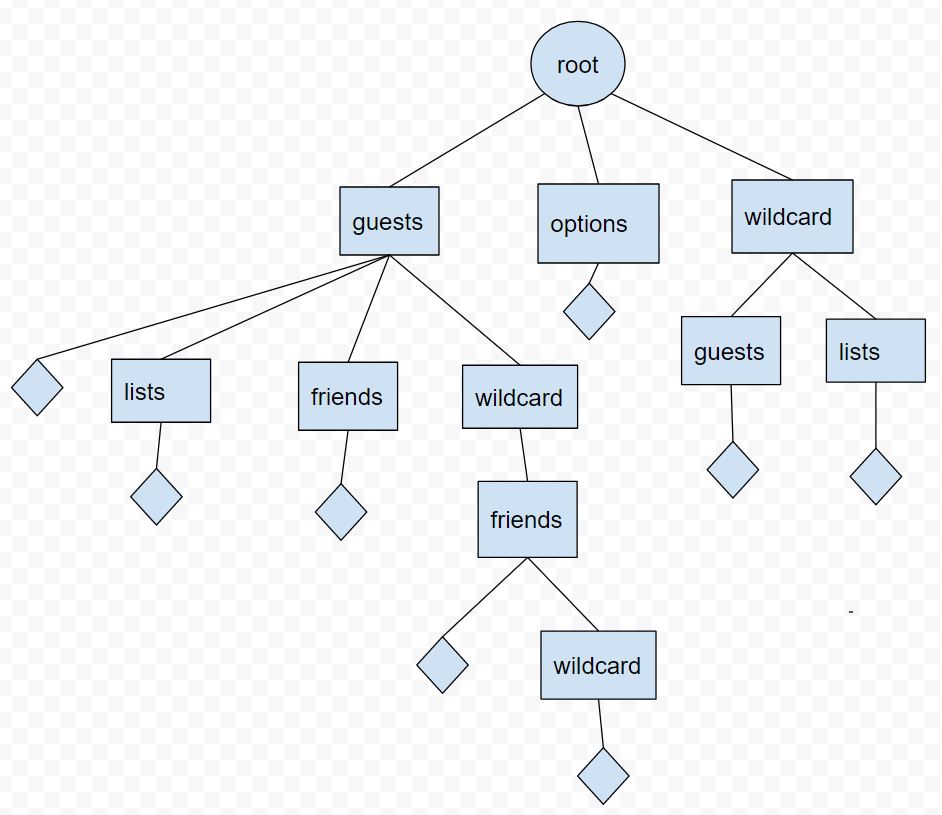

Спасибо за любую помощь!

Answer 1

Наихудшее время поиска будет O(E+N), где E - число, если ребра, а N - количество узлов. Потому что мы не знаем, сколько узлов на каждом уровне. Таким образом, по вашему алгоритму вы находите первый узел в нужной последовательности, выполняя поиск по уровню, так как у вас нет параметров, чтобы проверить, проходит ли нужный путь. (Я знаю, что число узлов будет уменьшаться каждый раз, когда я опускаюсь на один уровень, но насколько это неопределенно в этом случае) Это даже не n-массив.

Подстановочный знак не поможет уменьшить временную сложность наихудшего случая и будет неуверен, чтобы узнать лучший случай дерева. Проверка группового символа занимает постоянное время и не учитывается во время выполнения.

Теперь алгоритм выглядит немного запутанным, что вы будете делать, когда у вас есть два варианта

1) у вас есть естественный совпадающий узел 2) у вас есть шаблонный узел.

На том же уровне, куда вы пойдете? Предположим, мы идем в том направлении, в котором вы впервые встретились. Но что, если это не фактический путь, который вы узнаете на последнем узле, чтобы вы вернули его назад. Чтобы избежать этого, вы будете хранить отметку о количестве доступных путей на каждом уровне по BFS и выполнять поиск. Таким образом, сложность времени в наихудшем случае будет O(E+N), если вы обработали все случаи.