Foldr и Foldl дальнейшие объяснения и примеры

Я смотрел на различные сгибы и сгибы в целом, а также несколько других, и они объясняют это довольно хорошо.

У меня все еще проблемы с тем, как лямбда будет работать в этом случае.

foldr (\y ys -> ys ++ [y]) [] [1,2,3]

Может ли кто-нибудь пройти этот шаг за шагом и попытаться объяснить это мне?

А также как бы foldl Работа?

Источник

6 ответов

Решение

С помощью

foldr f z []     = z
foldr f z (x:xs) = x `f` foldr f z xs

А также

k y ys = ys ++ [y]

Давайте распакуем:

foldr k [] [1,2,3]
= k 1 (foldr k [] [2,3]
= k 1 (k 2 (foldr k [] [3]))
= k 1 (k 2 (k 3 (foldr k [] [])))
= (k 2 (k 3 (foldr k [] []))) ++ [1]
= ((k 3 (foldr k [] [])) ++ [2]) ++ [1]
= (((foldr k [] []) ++ [3]) ++ [2]) ++ [1]
= ((([]) ++ [3]) ++ [2]) ++ [1]
= (([3]) ++ [2]) ++ [1]
= ([3,2]) ++ [1]
= [3,2,1]
Источник

Foldr это простая вещь:

foldr :: (a->b->b) -> b -> [a] -> b

Требуется функция, которая чем-то похожа на (:),

(:) :: a -> [a] -> [a]

и значение, которое похоже на пустой список [],

[] :: [a]

и заменяет каждый: и [] в некотором списке.

Это выглядит так:

foldr f e (1:2:3:[]) = 1 `f` (2 `f` (3 `f` e))

Вы также можете представить foldr как некоторый конечный автомат:

f - переход,

f :: input -> state -> state

и е - начальное состояние.

e :: state

foldr (foldRIGHT) запускает конечный автомат с переходом f и начальным состоянием e над списком входов, начиная с правого конца. Представьте, что в инфиксной записи f как человек, идущий справа налево.

foldl (foldLEFT) делает то же самое из-LEFT, но функция перехода, написанная в инфиксной записи, получает свой входной аргумент справа. Таким образом, машина использует список, начиная с левого конца. Пакман использует список из -LEFT с открытым ртом вправо, потому что рот (b->a->b) вместо (a->b->b).

foldl :: (b->a->b) -> b -> [a] -> b

Чтобы это было понятно, представьте функцию минус как переход:

foldl (-) 100 [1]         = 99 = ((100)-1)
foldl (-) 100 [1,2]       = 97 = (( 99)-2) = (((100)-1)-2)
foldl (-) 100 [1,2,3]     = 94 = (( 97)-3)
foldl (-) 100 [1,2,3,4]   = 90 = (( 94)-4)
foldl (-) 100 [1,2,3,4,5] = 85 = (( 90)-5)

foldr (-) 100 [1]         = -99 = (1-(100))
foldr (-) 100 [2,1]       = 101 = (2-(-99)) = (2-(1-(100)))
foldr (-) 100 [3,2,1]     = -98 = (3-(101))
foldr (-) 100 [4,3,2,1]   = 102 = (4-(-98))
foldr (-) 100 [5,4,3,2,1] = -97 = (5-(102))

Возможно, вы захотите использовать foldr в ситуациях, когда список может быть бесконечным, и когда оценка должна быть ленивой:

foldr (either (\l (ls,rs)->(l:ls,rs))
              (\r (ls,rs)->(ls,r:rs))
      ) ([],[]) :: [Either l r]->([l],[r])

И вы, вероятно, захотите использовать строгую версию foldl, которая является foldl', когда вы используете весь список для вывода. Это может работать лучше и может препятствовать возникновению исключений переполнения стека или нехватки памяти (в зависимости от компилятора) из-за очень длинных списков в сочетании с отложенной оценкой:

foldl' (+) 0 [1..100000000] = 5000000050000000
foldl  (+) 0 [1..100000000] = error "stack overflow or out of memory" -- dont try in ghci
foldr  (+) 0 [1..100000000] = error "stack overflow or out of memory" -- dont try in ghci

Первый - шаг за шагом - создает одну запись в списке, оценивает ее и использует ее.

Второй создает сначала очень длинную формулу, тратя память на ((...((0+1)+2)+3)+...), а затем оценивает все это.

Третий похож на второй, но с другой формулой.

Источник

Определение foldr является:

foldr f z []     = z
foldr f z (x:xs) = f x (foldr f z xs)

Итак, вот пошаговое сокращение вашего примера:

  foldr (\y ys -> ys ++ [y]) [] [1,2,3]
= (\y ys -> ys ++ [y]) 1 (foldr (\y ys -> ys ++ [y]) [] [2,3])
= (foldr (\y ys -> ys ++ [y]) [] [2,3]) ++ [1]
= (\y ys -> ys ++ [y]) 2 (foldr (\y ys -> ys ++ [y]) [] [3]) ++ [1]
= (foldr (\y ys -> ys ++ [y]) [] [3]) ++ [2] ++ [1]
= (\y ys -> ys ++ [y]) 3 (foldr (\y ys -> ys ++ [y]) [] []) ++ [2] ++ [1]
= (foldr (\y ys -> ys ++ [y]) [] []) ++ [3] ++ [2] ++ [1]
= [] ++ [3] ++ [2] ++ [1]
= [3,2,1]
Источник

Обозначение инфикса, вероятно, будет более понятным здесь.

Давайте начнем с определения:

foldr f z []     = z
foldr f z (x:xs) = x `f` (foldr f z xs)

Для краткости напишем g вместо (\y ys -> ys ++ [y]), Следующие строки эквивалентны:

foldr g [] [1,2,3]
1 `g` (foldr g [] [2,3])
1 `g` (2 `g` (foldr g [] [3]))
1 `g` (2 `g` (3 `g` (foldr g [] [])))
1 `g` (2 `g` (3 `g` []))
(2 `g` (3 `g` [])) ++ [1]
(3 `g` []) ++ [2] ++ [1]
[3] ++ [2] ++ [1]
[3,2,1]
Источник

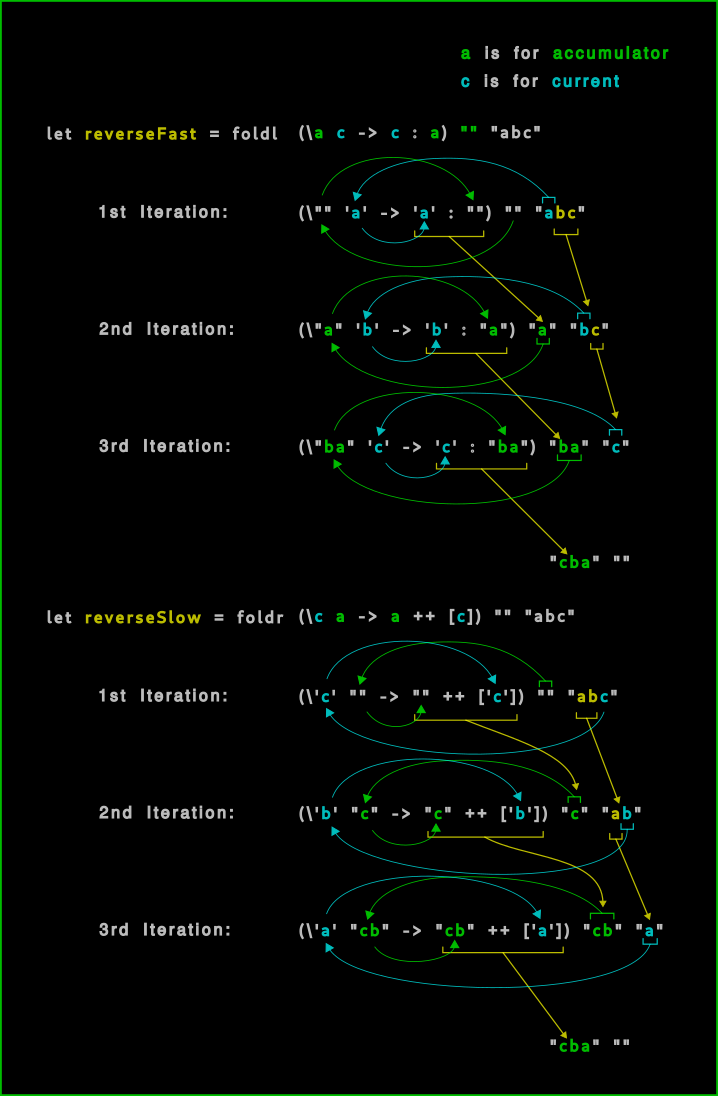
Я склонен запоминать вещи в движении, поэтому я представляю и визуализирую значения, летающие вокруг. Это мое внутреннее представление foldl и foldr.

Диаграмма ниже делает несколько вещей:

  1. называет аргументы функций сгиба интуитивно понятным (для меня) способом,
  2. показывает, с какого конца работает каждая конкретная складка (складка слева, складка справа),
  3. цветовая маркировка аккумулятора и текущих значений,
  4. отслеживает значения через лямбда-функцию, отображая их на следующую итерацию свертки.

Мнемонически я помню аргументы foldl в алфавитном порядке (\a c ->), а аргументы foldr должны быть в обратном алфавитном порядке (\c a ->). lозначает брать слева,rзначит брать справа.

Источник

Во-первых, я запомнил это с помощью операции ассоциативно-чувствительного вычитания :

      foldl (\a b -> a - b) 1 [2] = -1
foldr (\a b -> a - b) 1 [2] = 1

Во-вторых, foldl начинается с самого левого или первого элемента списка, тогда как foldrначинается с самого правого или последнего элемента списка. Выше это неочевидно, поскольку в списке всего один элемент.

Моя мнемоника такова: left или же right описывает две вещи:

  • размещение минуса ( -) символ
  • начальный элемент списка
Источник
Другие вопросы по тегам