Алгоритм для определения повторного схождения графа (аналогично общему поддереву?)

Question

Я работал над этой проблемой весь день, я переписываю один из наших устаревших продуктов, и мне трудно определить, как найти конкретный узел в моей блок-схеме. Эта проблема напоминает мне об университете, но я не могу придумать алгоритм для решения этой проблемы.

Я приложил 3 снимка экрана, чтобы помочь объяснить это, но основная проблема, учитывая ДА / НЕТ? узел принятия решений, найдите ближайший дочерний узел, который завершает ветвь.

Я работаю в C# .NET и JSON. В JSON у меня есть объект, который дает каждому узлу уникальный идентификатор, а также идентифицирует каждую "ссылку" от одного узла к следующему. Я хотел бы написать функцию (или несколько) для определения первого "конечного узла", заданного разветвленным узлом в C#. В настоящее время я встроил JSON в XML в C#.

Любые и всякие идеи поощряются, на самом деле не поиском кода, а подходом / алгоритмом.

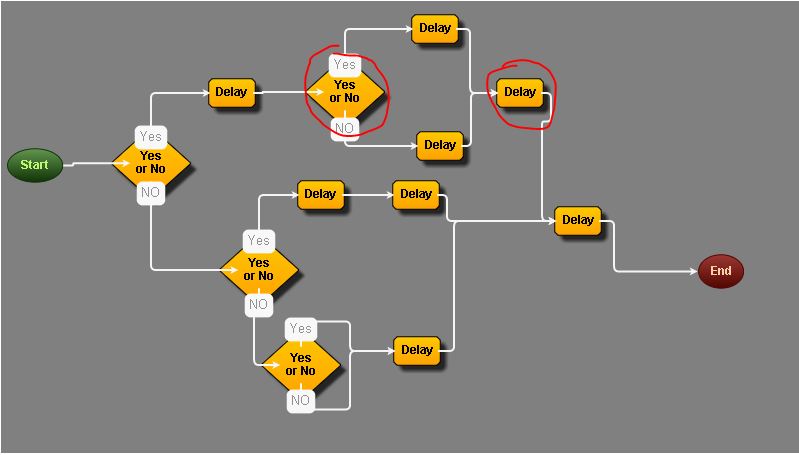
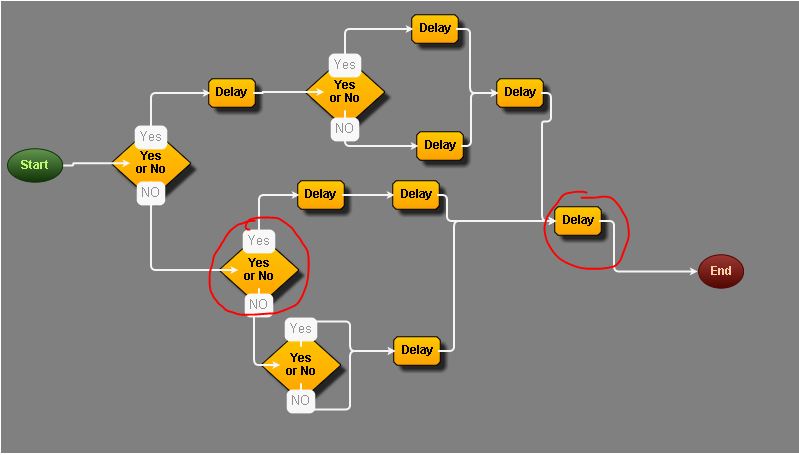
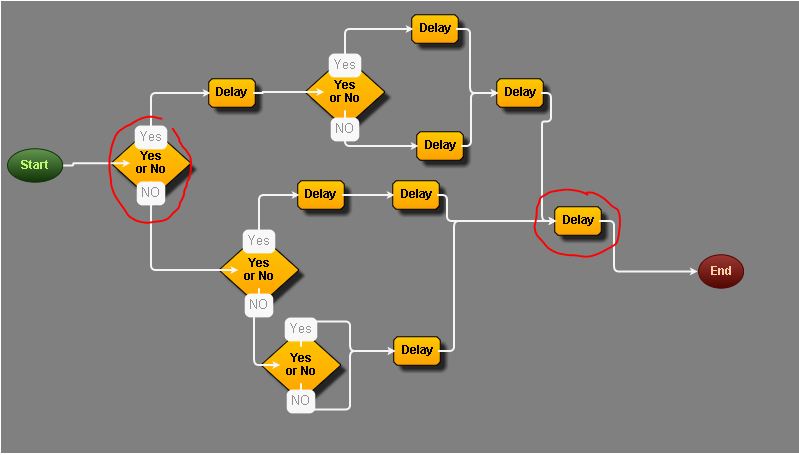
Прилагается вывод в формате jSON из диаграммы:

{ "class": "go.GraphLinksModel",
  "linkFromPortIdProperty": "fromPort",
  "linkToPortIdProperty": "toPort",
  "nodeDataArray": [ 
{"key":-1, "category":"Start", "loc":"169 288", "text":"Start"},
{"key":-2, "category":"End", "loc":"855 394", "text":"End"},
{"category":"Branch", "text":"Yes or No", "key":-4, "loc":"284.8837209302326 285.7848837209302"},
{"category":"DelayNode", "text":"Delay", "key":-3, "loc":"365.8837209302326 215.52345997177622"},
{"category":"Branch", "text":"Yes or No", "key":-5, "loc":"478.8837209302326 214.52345997177622"},
{"category":"DelayNode", "text":"Delay", "key":-6, "loc":"568.8837209302326 151.52345997177622"},
{"category":"DelayNode", "text":"Delay", "key":-7, "loc":"573.8837209302326 268.5234599717762"},
{"category":"DelayNode", "text":"Delay", "key":-8, "loc":"653.8837209302326 215.52345997177622"},
{"category":"Branch", "text":"Yes or No", "key":-9, "loc":"392.8837209302326 392.5234599717762"},
{"category":"DelayNode", "text":"Delay", "key":-10, "loc":"454.8837209302326 317.5234599717762"},
{"category":"DelayNode", "text":"Delay", "key":-11, "loc":"550.8837209302326 473.5234599717762"},
{"category":"DelayNode", "text":"Delay", "key":-12, "loc":"549.8837209302326 317.5234599717762"},
{"category":"DelayNode", "text":"Delay", "key":-13, "loc":"711.8837209302326 343.5234599717762"},
{"category":"Branch", "text":"Yes or No", "key":-14, "loc":"434.8837209302326 487.5234599717762"}
 ],
  "linkDataArray": [ 
{"from":-4, "to":-3, "fromPort":"T", "toPort":"L", "visible":true},
{"from":-1, "to":-4, "fromPort":"R", "toPort":"L"},
{"from":-3, "to":-5, "fromPort":"R", "toPort":"L"},
{"from":-5, "to":-6, "fromPort":"T", "toPort":"L", "visible":true},
{"from":-5, "to":-7, "fromPort":"B", "toPort":"L", "visible":true, "text":"NO"},
{"from":-6, "to":-8, "fromPort":"R", "toPort":"L"},
{"from":-7, "to":-8, "fromPort":"R", "toPort":"L"},
{"from":-4, "to":-9, "fromPort":"B", "toPort":"L", "visible":true, "text":"NO"},
{"from":-9, "to":-10, "fromPort":"T", "toPort":"L", "visible":true},
{"from":-10, "to":-12, "fromPort":"R", "toPort":"L"},
{"from":-11, "to":-13, "fromPort":"R", "toPort":"L"},
{"from":-12, "to":-13, "fromPort":"R", "toPort":"L"},
{"from":-8, "to":-13, "fromPort":"R", "toPort":"L"},
{"from":-13, "to":-2, "fromPort":"R", "toPort":"L"},
{"from":-9, "to":-14, "fromPort":"B", "toPort":"L", "visible":true, "text":"NO"},
{"from":-14, "to":-11, "fromPort":"T", "toPort":"L", "visible":true},
{"from":-14, "to":-11, "fromPort":"B", "toPort":"L", "visible":true, "text":"NO"}
 ]}

Answer 1

ОБНОВЛЕНИЕ: я нашел другое решение, на этот раз используя стандартное решение проблемы самого низкого общего предка. Смотрите мой другой ответ.

---

Как отмечается в комментариях к ответу Орен, Орен фактически ответил на вопрос "какой самый близкий узел может быть достигнут из обеих ветвей?" Но вопрос, на который на самом деле нужно ответить: "Какой самый близкий узел должен быть достигнут обеими ветвями?"

Решить эту проблему гораздо сложнее, и я не знаю эффективного решения на моей голове. Однако вот эскиз алгоритма, который будет работать.

Предположим, что данный узел принятия решений называется A, а WOLOG имеет двух дочерних элементов B и C. Тогда возникает вопрос: что это за узел, называемый G, который имеет эти два свойства:

• Каждый возможный путь от B до END и каждый возможный путь от C до END проходит через G.
• G - ближайший к B и C узел, имеющий первое свойство.

(Обратите внимание, что G может быть END. У нас может быть A ->B, A->C, B->END, C->END.)

Мы можем начать с набора кандидатов на возможные G достаточно легко. Выберите любой путь от B до END - выберите его наугад, если хотите - и поместите его узлы в хэш-набор. Затем выберите любой путь от C до END и поместите его узлы в хэш-набор. Пересечение этих двух множеств содержит G. Назовите множество пересечений Альфа.

Итак, теперь давайте удалим из Альфы все узлы, которые определенно не являются G. Для каждого узла N в наборе Альфа:

• Построить новый граф, идентичный исходному графу, но без N.
• Достигнут ли END из B или C в новом графике? Если да, то N определенно не является G. Если нет, добавьте N, чтобы установить бета-версию.

Если, когда мы закончим, бета-версия пуста, то G будет END.

В противном случае в бета-версии есть узлы. Каждый из этих узлов обладает свойством, что, если он будет удален, нет другого способа добраться из B или C в END. Ровно один из этих узлов должен быть ближе всего к B- если бы два были одинаково близки, то один из них не был бы необходим! - так же сделайте обход в ширину из B, и когда вы впервые встретитесь с узлом в бете, это ваш G.

Этот эскиз не выглядит быстрым, если график большой, но я уверен, что он будет работать. Мне было бы интересно узнать, есть ли лучшее решение.

Answer 2

Мне нравится ответ Алекса, и он кажется очень эффективным. Вот еще один способ решить вашу проблему, которая, как выясняется, на самом деле является проблемой самого низкого общего предка. Это чрезвычайно хорошо изученная проблема в теории графов; Сначала я просто этого не видел, потому что ты должен перевернуть все стрелки.

С этим решением вы выполняете дорогостоящую предварительную обработку один раз, и тогда у вас есть структура данных, с которой вы можете просто прочитать ответ.

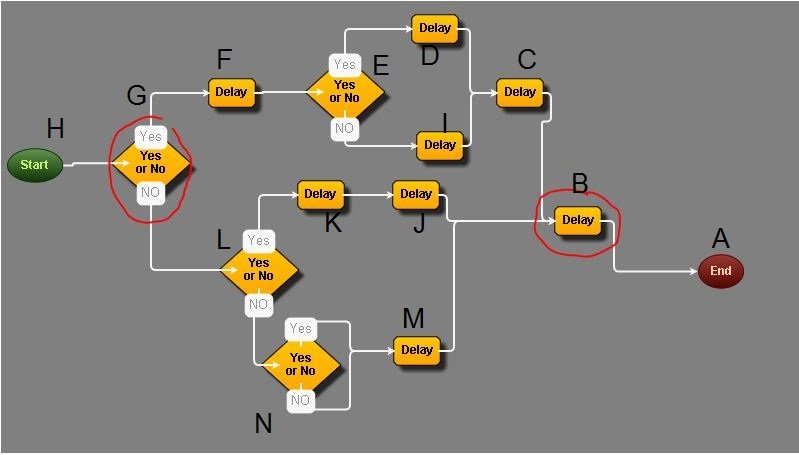
Я пометил узлы на вашем графике. Сначала вы обращаете все стрелки, а затем выстраиваете эйлерово обход полученного DAG, на каждом шаге вспоминая, как далеко вы находитесь от "корня" (конца).

Эйлерово прохождение гласит: "Приходи в себя, возвращайся к соседу, посещай себя, посещай соседа,… посещай себя". То есть, если бы мы писали это на C#, мы бы сказали что-то вроде:

void Eulerian(Node n, int i, List<Tuple<Node, int>> traversal)
{
    traversal.Add(Tuple.Create(node, i));
    foreach(Node neighbour in node.Neighbours)
    {
        Eulerian(neighbour, i + 1, traversal);
        traversal.Add(Tuple.Create(node, i));
    }
}

Эйлеровый обход - это обход, который вы бы на самом деле предприняли, если бы шли по графику.

График, который вы привели в качестве примера, имеет следующий эйлеровский обход, когда вы переворачиваете все стрелки и начинаете с КОНЦА.

A0 B1 C2 D3 E4 F5 G6 H7 G6 F5 E4 D3 C2 I3 E4 F5 G6 H7 G6 F5 E4 I3 C2 
B1 J2 K3 L4 G5 H6 G5 L4 K3 J2 B1 M2 N3 L4 G5 H6 G5 L4 N3 M2 N3 L4 G5 
H6 G5 L4 N3 M2 B1 A0

Ответ на ваш вопрос теперь можно прочитать из прохождения. В ваших примерах у вас есть узлы решения E, L и G.

Для E: найдите первое и последнее вхождения E в обход. Теперь ищите узлы между этими двумя в обходе для поиска с наименьшим числом. Это С, со счетом 2.

Для L: найдите первое и последнее вхождения L в обход. Узел с наименьшим числом между ними - B, со счетом 1.

Для G: снова узел с самым низким показателем между первым и последним появлением G является B.

Вычисление обхода может быть дорогим, если график большой, но приятно то, что вам нужно сделать это только один раз. После этого это просто проблема линейного поиска. (И вы могли бы сделать это проблемой сублинейного поиска, если бы вы действительно этого хотели, но это кажется большой дополнительной работой.)

Answer 3

Если я понимаю проблему, вы пытаетесь найти первый общий узел между поддеревьями "да" и "нет". В этом случае простым способом сделать это будет обход в ширину поддерева yes, добавление каждого элемента в список. Затем выполните обход в ширину или поддерево no, останавливаясь, когда элемент этого поддерева появляется в списке "yes".

Answer 4

Это можно сделать за O(V + E), используя два поиска в ширину / глубину.

Сначала давайте охарактеризуем проблему. Нам дан график, начальный узел A и конечный узел END. Как определено @EricLippert (и немного адаптировано мной, поскольку мы можем эквивалентно использовать A вместо B и C), мы ищем узел G с этими двумя свойствами:

• Каждый возможный путь от А до КОНЦА проходит через G.
• G - ближайший к A узел, имеющий первое свойство.

Во-первых, мы находим путь от A до END, используя поиск X-first. Пусть P = (p1, p2, p3, ..., pk) с p1 = A и pk = END будет этим путем, и пронумеровайте их 1, 2, ..., k (так что pi имеет номер i). Сохраните эти числа с узлами на графике. Удалите ребра, используемые P из графика. Выполните еще один X-первый поиск из A и найдите узел с наибольшим номером pi, который доступен из A. Мы слегка адаптируем этот поиск: каждый раз, когда мы находим достижимый узел pj, который выше, чем предыдущий узел с наивысшим достижимым pk, мы добавляем все ребра в подпуть (pk, pk+1, ..., pj) обратно в граф и пометить все эти промежуточные узлы как достижимые, а также добавить все узлы, которые были недоступны ранее, в используемую очередь / стек в нашем X-первом поиске обработки. Верните пи, найденный таким образом.

Теперь мы покажем, что pi удовлетворяет условиям G. Предположим (с целью достижения противоречия) у нас есть путь S=(s1, s2, s3, ..., sj) с s1 = A и sj = END, что не проходит через пи. Некоторые префиксы (s1, s2, s3, ... sm) этого пути согласуются с нашим путем P, поэтому s1=p1, s2=p2, ..., sm=pm, но sm+1!= Pm+1. Так как S не прошел через pi, а pi был достигнут нашим вторым поиском X-first, sm становится достижимым в нашем втором поиске X-first, когда мы добавляем ребра, используемые (s1, s2, s3, ..., sm), Поэтому наш второй X-первый поиск будет также проходить по остальной части пути S, пока он не достигнет либо END, либо какое-либо ребро, используемое в S (pr, pr+1), будет лежать на пути P, но r > i, и, следовательно, это ребро удален. Однако тогда мы обнаружили бы, что pr (или END) достижимо и r > i, поэтому мы бы не вернули pi, что противоречит. Следовательно, все пути проходят через пи.

Теперь предположим, что есть некоторый узел G, который имеет свойства, указанные выше, но находится "ближе" к A, чем pi. Поскольку все пути проходят через G', P также проходит через G', поэтому есть некоторые v с pv=G'и v

Первый X-первый поиск занимает O(V + E) времени. Второй также занимает время O(V + E): все узлы добавляются в очередь / стек не более одного раза, поэтому время выполнения сохраняется, даже если мы добавляем ребра обратно в граф; окончательное число ребер также не превышает число ребер исходного графа. Поддержание индексов пути и самого высокого найденного пока индекса занимает также время O(V + E), поэтому мы заключаем, что наш алгоритм работает за время O(V + E).

Answer 5

Так что я больше задумался над этим, принимая во внимание некоторые ответы, представленные здесь, я не совсем начал писать код для него, но, учитывая один из ответов, я немного изменил его в псевдокод.

Я думаю, что более эффективным подходом было бы отслеживать все результаты для любого узла ветви в общей паре словарь-переменная (ключ, значение). Есть мысли по поводу этого подхода? Я должен упомянуть одну вещь: граф никогда не должен увеличиваться до более чем 25 узлов.

//call this function for all nodes with 2 children
int getFirstCommonAllpathEndNode(currentNodeId, xml, endNodeId){

    Array[] possibleNodeIds;
    //traverse child nodes
    foreach(childnode of CurrentNode.TopPortChildNode){
        if(childNode has 2 ports)
        {
            possibleNodeIds.add( getFirstCommonAllPathEndNode(childNode.id, xml, endnodeId));
        }
        else{
            possibleNodeIds.add(childNode.Id);
        }
    }

    foreach(childnode of CurrentNode.BottomPortChildNode){
        if(childNode has 2 ports)
        {
            //recursive call for this branch to get it's first common all path end node
            var someNodeId = getFirstCommonAllPathEndNode(childNode.id, xml, endnodeId) 
            if(possibleNodeIds contains someNodeId) 
                return someNodeId;
            //otherwise skip forward to someNodeId as next node to process in for loop
        }
        else{
            if (possibleNodeIds contains childNode.Id)
                return childNode.id
        }
    }
    //return the endNode if nothing else is satisfied. although this code should never be hit
    return endNodeId;
}