Использование FiPy и Mayavi для решения уравнения диффузии в 3D
Я заинтересован в решении,
\frac{\delta \phi}{\delta t} - D \nabla^2 \phi - \alpha \phi - \gamma \phi = 0
Следующее работает, но у меня есть несколько вопросов:
- Можно ли повысить производительность с помощью FiPy? Я чувствую себя как
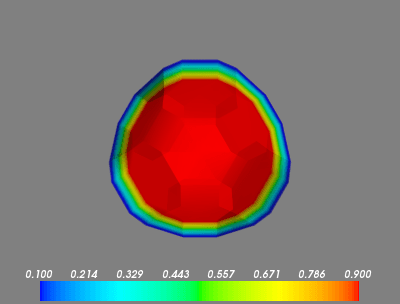
nx, ny, nzБункеры здесь очень маленькие, несмотря на длительное время вычислений.Я не понимаю, почему массивыX, Y, and Zтакие большие. - Обратите внимание, что в первом кадре мы увеличены. Как я могу заставить экстенты автоматически
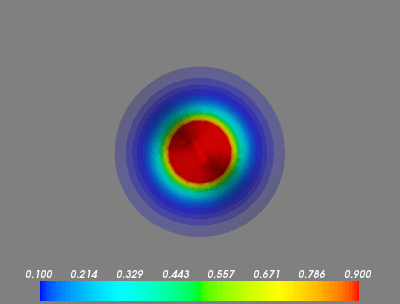
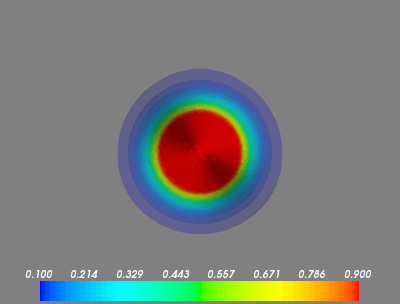
[0..nx, 0..ny, 0..nz]на всех участках? - Данные для первого кадра - это сфера точек со значениями
1.0окружен0.0, Почему появляется градиент? Mayavi интерполирует? Если так, как я могу отключить это?
Код:
from fipy import *
import mayavi.mlab as mlab
import numpy as np
import time
# Spatial parameters
nx = ny = nz = 30 # bins
dx = dy = dz = 1 # Must this be an integer?
L = nx * dx
# Diffusion and time step
D = 1.
dt = 10.0 * dx**2 / (2. * D)
steps = 4
# Initial value and radius of concentration
phi0 = 1.0
r = 3.0
# Rates
alpha = 1.0 # Source coeficcient
gamma = .01 # Sink coeficcient
mesh = Grid3D(nx=nx, ny=ny, nz=nz, dx=dx, dy=dy, dz=dz)
X, Y, Z = mesh.cellCenters # These are large arrays
phi = CellVariable(mesh=mesh, name=r"$\phi$", value=0.)
src = phi * alpha # Source term (zeroth order reaction)
degr = -gamma * phi # Sink term (degredation)
eq = TransientTerm() == DiffusionTerm(D) + src + degr
# Initial concentration is a sphere located in the center of a bounded cube
phi.setValue(1.0, where=( ((X-nx/2))**2 + (Y-ny/2)**2 + (Z-nz/2)**2 < r**2) )
# Solve
start_time = time.time()
results = [phi.getNumericValue().copy()]
for step in range(steps):
eq.solve(var=phi, dt=dt)
results.append(phi.getNumericValue().copy())
print 'Time elapsed:', time.time() - start_time
# Plot
for i, res in enumerate(results):
fig = mlab.figure()
res = res.reshape(nx, ny, nz)
mlab.contour3d(res, opacity=.3, vmin=0, vmax=1, contours=100, transparent=True, extent=[0, 10, 0, 10, 0, 10])
mlab.colorbar()
mlab.savefig('diffusion3d_%i.png'%(i+1))
mlab.close()
Прошедшее время: 68,2 секунды
1 ответ
По твоему вопросу трудно сказать, но в процессе диагностики я обнаружил, что
LinearLUSolverмасштабируется очень плохо по мере увеличения масштабов проблемы (см. https://github.com/usnistgov/fipy/issues/474).Для этой симметричной задачи PySparse должен использовать решатель PCG, а Trilinos должен использовать GMRES. Если вы не установили ни один из них, тогда вы получите разреженный решатель SciPy, который по умолчанию равен LU (я не знаю почему; что-то для нас нужно изучить), и в 3D все будет очень медленно. Попробуйте добавить
solver=LinearGMRESSolver()на вашeq.solve(...)заявление.Что касается размеров X, Y и Z, вы объявили куб 30*30*30 ячеек, поэтому каждый из координатных векторов центра ячейки будет иметь длину 27000 элементов. У вас было другое ожидание
cellCenters?Я предлагаю вам создать подкласс нашего класса MayaviDaemon или хотя бы посмотреть, как он настраивает отображение в Mayavi. Короче говоря, мы установили
data_set_clipperдо желаемых границ.Я не знаю.