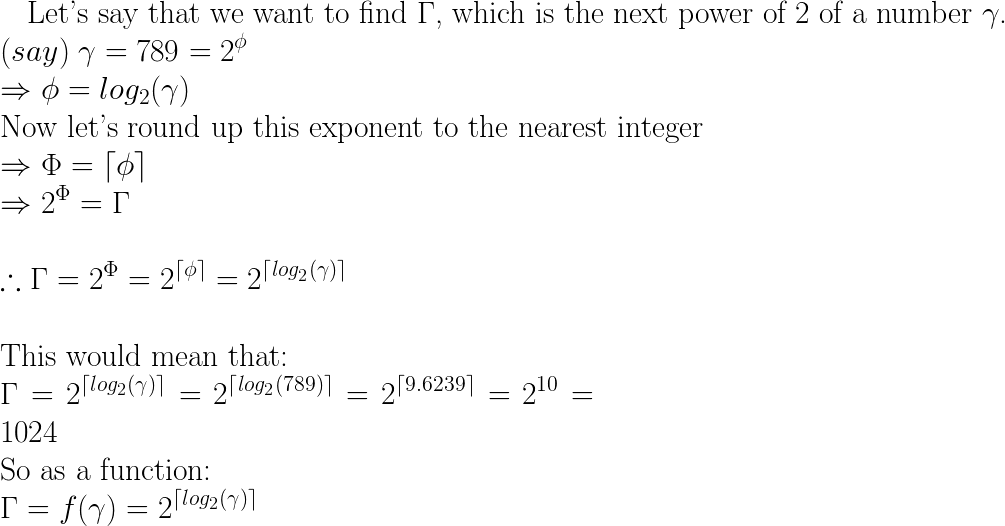Округление до следующей степени 2
Я хочу написать функцию, которая возвращает ближайшую следующую степень 2 числа. Например, если мой ввод 789, вывод должен быть 1024. Есть ли способ достичь этого без использования циклов, а только с помощью некоторых побитовых операторов?
31 ответ
Проверьте взломанные бит-хаки. Вам нужно получить логарифм с основанием 2, а затем добавить 1 к этому. Пример для 32-битного значения:
Округление до следующей высшей степени 2
unsigned int v; // compute the next highest power of 2 of 32-bit v v--; v |= v >> 1; v |= v >> 2; v |= v >> 4; v |= v >> 8; v |= v >> 16; v++;
Расширение на другие значения ширины должно быть очевидным.
next = pow(2, ceil(log(x)/log(2)));
Это работает путем нахождения числа, которое вы бы увеличили на 2, чтобы получить x (возьмите журнал числа и разделите на журнал нужной базы, подробнее см. Википедию). Затем округлите это до ceil, чтобы получить ближайшее целое число.
Это более общий метод (т. Е. Более медленный!) Метод, чем побитовые методы, связанные в других местах, но полезно знать математику, а?
Я думаю, что это тоже работает:
int power = 1;
while(power < x)
power*=2;
И ответ power,
unsigned long upper_power_of_two(unsigned long v)
{
v--;
v |= v >> 1;
v |= v >> 2;
v |= v >> 4;
v |= v >> 8;
v |= v >> 16;
v++;
return v;
}
Если вы используете GCC, вы можете взглянуть на Оптимизацию функции next_pow2() от Lockless Inc.. На этой странице описан способ использования встроенной функции. builtin_clz() (считать начальный ноль) и позже использовать непосредственно инструкцию ассемблера x86 (ia32) bsr (битовое сканирование в обратном порядке), так же, как это описано в ссылке другого ответа на сайт Gamedev. Этот код может быть быстрее, чем описано в предыдущем ответе.
Кстати, если вы не собираетесь использовать инструкцию на ассемблере и 64-битный тип данных, вы можете использовать это
/**
* return the smallest power of two value
* greater than x
*
* Input range: [2..2147483648]
* Output range: [2..2147483648]
*
*/
__attribute__ ((const))
static inline uint32_t p2(uint32_t x)
{
#if 0
assert(x > 1);
assert(x <= ((UINT32_MAX/2) + 1));
#endif
return 1 << (32 - __builtin_clz (x - 1));
}
В стандартном
c++20 это включено в
<bit>. Ответ прост
#include <bit>
unsigned long upper_power_of_two(unsigned long v)
{
return std::bit_ceil(v);
}
ПРИМЕЧАНИЕ . Решение, которое я дал, предназначено для
c++, нет
c, Я бы ответил на этот вопрос, но он был закрыт как дубликат этого!
Еще один, хотя я использую цикл, но это гораздо быстрее, чем математические операнды
Мощность двух "напольного" варианта:
int power = 1;
while (x >>= 1) power <<= 1;
Мощность двух "потолочных" вариантов:
int power = 2;
x--; // <<-- UPDATED
while (x >>= 1) power <<= 1;
ОБНОВИТЬ
Как уже упоминалось в комментариях, была ошибка в ceil где его результат был неверным.
Вот полные функции:
unsigned power_floor(unsigned x) {
int power = 1;
while (x >>= 1) power <<= 1;
return power;
}
unsigned power_ceil(unsigned x) {
if (x <= 1) return 1;
int power = 2;
x--;
while (x >>= 1) power <<= 1;
return power;
}
Для любого неподписанного типа, основанного на Bit Twiddling Hacks:
#include <climits>
#include <type_traits>
template <typename UnsignedType>
UnsignedType round_up_to_power_of_2(UnsignedType v) {
static_assert(std::is_unsigned<UnsignedType>::value, "Only works for unsigned types");
v--;
for (size_t i = 1; i < sizeof(v) * CHAR_BIT; i *= 2) //Prefer size_t "Warning comparison between signed and unsigned integer"
{
v |= v >> i;
}
return ++v;
}
Там действительно нет цикла, так как компилятор знает во время компиляции количество итераций.
Несмотря на то, что вопрос помечен как c здесь мои пять центов. К счастью, C++ 20 будет включать std::ceil2 а также std::floor2 (см. здесь). это consexpr Функции шаблона, текущая реализация GCC использует сдвиг битов и работает с любым целым типом без знака.
Для поплавков IEEE вы сможете сделать что-то подобное.
int next_power_of_two(float a_F){
int f = *(int*)&a_F;
int b = f << 9 != 0; // If we're a power of two this is 0, otherwise this is 1
f >>= 23; // remove factional part of floating point number
f -= 127; // subtract 127 (the bias) from the exponent
// adds one to the exponent if were not a power of two,
// then raises our new exponent to the power of two again.
return (1 << (f + b));
}
Если вам нужно целочисленное решение и вы можете использовать встроенную сборку, BSR выдаст вам log2 целого числа на x86. Он подсчитывает, сколько правильных битов установлено, что в точности равно log2 этого числа. Другие процессоры имеют аналогичные инструкции (часто), такие как CLZ, и в зависимости от вашего компилятора может быть встроенное, чтобы сделать работу за вас.
Вот мое решение на C. Надеюсь, это поможет!
int next_power_of_two(int n) {
int i = 0;
for (--n; n > 0; n >>= 1) {
i++;
}
return 1 << i;
}
В x86 вы можете использовать инструкции по обработке битов sse4, чтобы сделать это быстро.
//assume input is in eax
popcnt edx,eax
lzcnt ecx,eax
cmp edx,1
jle @done //popcnt says its a power of 2, return input unchanged
mov eax,2
shl eax,cl
@done: rep ret
В c вы можете использовать соответствующие встроенные функции.
Для полноты здесь приведена реализация с плавающей точкой в болотном стандарте C.
double next_power_of_two(double value) {
int exp;
if(frexp(value, &exp) == 0.5) {
// Omit this case to round precise powers of two up to the *next* power
return value;
}
return ldexp(1.0, exp);
}
/*
** http://graphics.stanford.edu/~seander/bithacks.html#IntegerLog
*/
#define __LOG2A(s) ((s &0xffffffff00000000) ? (32 +__LOG2B(s >>32)): (__LOG2B(s)))
#define __LOG2B(s) ((s &0xffff0000) ? (16 +__LOG2C(s >>16)): (__LOG2C(s)))
#define __LOG2C(s) ((s &0xff00) ? (8 +__LOG2D(s >>8)) : (__LOG2D(s)))
#define __LOG2D(s) ((s &0xf0) ? (4 +__LOG2E(s >>4)) : (__LOG2E(s)))
#define __LOG2E(s) ((s &0xc) ? (2 +__LOG2F(s >>2)) : (__LOG2F(s)))
#define __LOG2F(s) ((s &0x2) ? (1) : (0))
#define LOG2_UINT64 __LOG2A
#define LOG2_UINT32 __LOG2B
#define LOG2_UINT16 __LOG2C
#define LOG2_UINT8 __LOG2D
static inline uint64_t
next_power_of_2(uint64_t i)
{
#if defined(__GNUC__)
return 1UL <<(1 +(63 -__builtin_clzl(i -1)));
#else
i =i -1;
i =LOG2_UINT64(i);
return 1UL <<(1 +i);
#endif
}
Если вы не хотите рисковать сферой неопределенного поведения, входное значение должно быть между 1 и 2^63. Макрос также полезен для установки константы во время компиляции.
Эффективное Microsoft (например, Visual Studio 2017) специальное решение на C / C++ для целочисленного ввода. Обрабатывает случай ввода, точно совпадающего со степенью двойки, уменьшая его перед проверкой расположения старшего значащего 1 бита.
inline unsigned int ExpandToPowerOf2(unsigned int Value)
{
unsigned long Index;
_BitScanReverse(&Index, Value - 1);
return (1U << (Index + 1));
}
// - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
#if defined(WIN64) // The _BitScanReverse64 intrinsic is only available for 64 bit builds because it depends on x64
inline unsigned long long ExpandToPowerOf2(unsigned long long Value)
{
unsigned long Index;
_BitScanReverse64(&Index, Value - 1);
return (1ULL << (Index + 1));
}
#endif
В результате получается около 5 встроенных инструкций для процессора Intel, аналогичных приведенным ниже:
dec eax
bsr rcx, rax
inc ecx
mov eax, 1
shl rax, cl
По-видимому, компилятор Visual Studio C++ не предназначен для оптимизации этого для значений времени компиляции, но он не такой, как там много инструкций.
Редактировать:
Если вы хотите, чтобы входное значение 1 приводило к 1 (2 к нулевой степени), небольшая модификация приведенного выше кода по-прежнему генерирует прямые инструкции без ветвления.
inline unsigned int ExpandToPowerOf2(unsigned int Value)
{
unsigned long Index;
_BitScanReverse(&Index, --Value);
if (Value == 0)
Index = (unsigned long) -1;
return (1U << (Index + 1));
}
Создает еще несколько инструкций. Хитрость в том, что Index может быть заменен тестом с последующей инструкцией cmove.
Пытаюсь найти для этого «окончательное» решение. Следующий код
предназначен для языка C (не C++),
использует встроенные компилятора для получения эффективного кода ( компонентыинструкция CLZ или BSR ), если компилятор поддерживает какой-либо,
является переносимым (стандартный C и без сборки), за исключением встроенных модулей, и
Насколько мне известно, затрагивает все неопределенные варианты поведения.
Если вы пишете на C ++, вы можете соответствующим образом скорректировать код. Обратите внимание, что C++20 вводит std :: bit_ceil, который делает то же самое, за исключением того, что поведение может быть неопределенным при определенных условиях.
#include <limits.h>
#ifdef _MSC_VER
# if _MSC_VER >= 1400
/* _BitScanReverse is introduced in Visual C++ 2005 and requires
<intrin.h> (also introduced in Visual C++ 2005). */
#include <intrin.h>
#pragma intrinsic(_BitScanReverse)
#pragma intrinsic(_BitScanReverse64)
# define HAVE_BITSCANREVERSE 1
# endif
#endif
/* Macro indicating that the compiler supports __builtin_clz().
The name HAVE_BUILTIN_CLZ seems to be the most common, but in some
projects HAVE__BUILTIN_CLZ is used instead. */
#ifdef __has_builtin
# if __has_builtin(__builtin_clz)
# define HAVE_BUILTIN_CLZ 1
# endif
#elif defined(__GNUC__)
# if (__GNUC__ > 3)
# define HAVE_BUILTIN_CLZ 1
# elif defined(__GNUC_MINOR__)
# if (__GNUC__ == 3 && __GNUC_MINOR__ >= 4)
# define HAVE_BUILTIN_CLZ 1
# endif
# endif
#endif
/**
* Returns the smallest power of two that is not smaller than x.
*/
unsigned long int next_power_of_2_long(unsigned long int x)
{
if (x <= 1) {
return 1;
}
x--;
#ifdef HAVE_BITSCANREVERSE
if (x > (ULONG_MAX >> 1)) {
return 0;
} else {
unsigned long int index;
(void) _BitScanReverse(&index, x);
return (1UL << (index + 1));
}
#elif defined(HAVE_BUILTIN_CLZ)
if (x > (ULONG_MAX >> 1)) {
return 0;
}
return (1UL << (sizeof(x) * CHAR_BIT - __builtin_clzl(x)));
#else
/* Solution from "Bit Twiddling Hacks"
<http://www.graphics.stanford.edu/~seander/bithacks.html#RoundUpPowerOf2>
but converted into a loop for smaller code size. */
{
unsigned int shift;
for (shift = 1; shift < sizeof(x) * CHAR_BIT; shift <<= 1) {
x |= (x >> shift);
}
}
return (x + 1);
#endif
}
unsigned int next_power_of_2(unsigned int x)
{
if (x <= 1) {
return 1;
}
x--;
#ifdef HAVE_BITSCANREVERSE
if (x > (UINT_MAX >> 1)) {
return 0;
} else {
unsigned long int index;
(void) _BitScanReverse(&index, (unsigned long int) x);
return (1U << (index + 1));
}
#elif defined(HAVE_BUILTIN_CLZ)
if (x > (UINT_MAX >> 1)) {
return 0;
}
return (1U << (sizeof(x) * CHAR_BIT - __builtin_clz(x)));
#else
{
unsigned int shift;
for (shift = 1; shift < sizeof(x) * CHAR_BIT; shift <<= 1) {
x |= (x >> shift);
}
}
return (x + 1);
#endif
}
unsigned long long next_power_of_2_long_long(unsigned long long x)
{
if (x <= 1) {
return 1;
}
x--;
#ifdef HAVE_BITSCANREVERSE
if (x > (ULLONG_MAX >> 1)) {
return 0;
} else {
/* assert(sizeof(__int64) >= sizeof(long long)); */
unsigned long int index;
(void) _BitScanReverse64(&index, (unsigned __int64) x);
return (1ULL << (index + 1));
}
#elif defined(HAVE_BUILTIN_CLZ)
if (x > (ULLONG_MAX >> 1)) {
return 0;
}
return (1ULL << (sizeof(x) * CHAR_BIT - __builtin_clzll(x)));
#else
{
unsigned int shift;
for (shift = 1; shift < sizeof(x) * CHAR_BIT; shift <<= 1) {
x |= (x >> shift);
}
}
return (x + 1);
#endif
}
Переносимое решение на C#:
long value = 27
long nextPowerOfTwo = 1 << (int)Math.Ceiling(Math.Log2(value));
nextPowerOfTwo 32 года.
Math.Ceiling(Math.Log2(value)) вычисляет экспоненту следующей степени двойки,
1 << вычисляет реальное значение путем сдвига битов.
Моя constexpr-версия CLP2 (C++14)
#include <iostream>
#include <climits>
#include <type_traits>
#ifndef CHAR_BIT
#define CHAR_BIT 8
#endif
namespace clp2_impl {
template <typename Int>
constexpr auto make(std::make_unsigned_t<Int> n, uintmax_t i = 1) noexcept -> decltype(n)
{ return i < sizeof(Int) * CHAR_BIT ? make<Int>(n | (n >> i), i << 1) : n; }
}
/// Closest least integral power of 2
template <typename Int, std::enable_if_t<std::is_integral<Int>::value,int> = 0>
constexpr auto clp2(Int n) noexcept
{ return clp2_impl::make<Int>(n-1) + 1; }
struct A
{
static constexpr int v = clp2(789);
};
int main()
{
std::cout << A::v; // Output: 1024
return 0;
}
Поддержка многих процессорных архитектур log base 2 или очень похожая операция - count leading zeros, Многие компиляторы имеют встроенные функции для этого. Смотрите https://en.wikipedia.org/wiki/Find_first_set
Предполагая, что у вас есть хороший компилятор, и он может немного перевернуться перед рукой, которая сейчас выше меня, но в любом случае это работает!!!
// http://graphics.stanford.edu/~seander/bithacks.html#IntegerLogObvious
#define SH1(v) ((v-1) | ((v-1) >> 1)) // accidently came up w/ this...
#define SH2(v) ((v) | ((v) >> 2))
#define SH4(v) ((v) | ((v) >> 4))
#define SH8(v) ((v) | ((v) >> 8))
#define SH16(v) ((v) | ((v) >> 16))
#define OP(v) (SH16(SH8(SH4(SH2(SH1(v))))))
#define CB0(v) ((v) - (((v) >> 1) & 0x55555555))
#define CB1(v) (((v) & 0x33333333) + (((v) >> 2) & 0x33333333))
#define CB2(v) ((((v) + ((v) >> 4) & 0xF0F0F0F) * 0x1010101) >> 24)
#define CBSET(v) (CB2(CB1(CB0((v)))))
#define FLOG2(v) (CBSET(OP(v)))
Тестовый код ниже:
#include <iostream>
using namespace std;
// http://graphics.stanford.edu/~seander/bithacks.html#IntegerLogObvious
#define SH1(v) ((v-1) | ((v-1) >> 1)) // accidently guess this...
#define SH2(v) ((v) | ((v) >> 2))
#define SH4(v) ((v) | ((v) >> 4))
#define SH8(v) ((v) | ((v) >> 8))
#define SH16(v) ((v) | ((v) >> 16))
#define OP(v) (SH16(SH8(SH4(SH2(SH1(v))))))
#define CB0(v) ((v) - (((v) >> 1) & 0x55555555))
#define CB1(v) (((v) & 0x33333333) + (((v) >> 2) & 0x33333333))
#define CB2(v) ((((v) + ((v) >> 4) & 0xF0F0F0F) * 0x1010101) >> 24)
#define CBSET(v) (CB2(CB1(CB0((v)))))
#define FLOG2(v) (CBSET(OP(v)))
#define SZ4 FLOG2(4)
#define SZ6 FLOG2(6)
#define SZ7 FLOG2(7)
#define SZ8 FLOG2(8)
#define SZ9 FLOG2(9)
#define SZ16 FLOG2(16)
#define SZ17 FLOG2(17)
#define SZ127 FLOG2(127)
#define SZ1023 FLOG2(1023)
#define SZ1024 FLOG2(1024)
#define SZ2_17 FLOG2((1ul << 17)) //
#define SZ_LOG2 FLOG2(SZ)
#define DBG_PRINT(x) do { std::printf("Line:%-4d" " %10s = %-10d\n", __LINE__, #x, x); } while(0);
uint32_t arrTble[FLOG2(63)];
int main(){
int8_t n;
DBG_PRINT(SZ4);
DBG_PRINT(SZ6);
DBG_PRINT(SZ7);
DBG_PRINT(SZ8);
DBG_PRINT(SZ9);
DBG_PRINT(SZ16);
DBG_PRINT(SZ17);
DBG_PRINT(SZ127);
DBG_PRINT(SZ1023);
DBG_PRINT(SZ1024);
DBG_PRINT(SZ2_17);
return(0);
}
Выходы:
Line:39 SZ4 = 2
Line:40 SZ6 = 3
Line:41 SZ7 = 3
Line:42 SZ8 = 3
Line:43 SZ9 = 4
Line:44 SZ16 = 4
Line:45 SZ17 = 5
Line:46 SZ127 = 7
Line:47 SZ1023 = 10
Line:48 SZ1024 = 10
Line:49 SZ2_16 = 17
Вариант ответа @YannDroneaud, действительный для x==1, только для платформ x86, компиляторов, gcc или clang:
__attribute__ ((const))
static inline uint32_t p2(uint32_t x)
{
#if 0
assert(x > 0);
assert(x <= ((UINT32_MAX/2) + 1));
#endif
int clz;
uint32_t xm1 = x-1;
asm(
"lzcnt %1,%0"
:"=r" (clz)
:"rm" (xm1)
:"cc"
);
return 1 << (32 - clz);
}
Вот то, что я использую, чтобы это было константным выражением, если ввод является константным выражением.
#define uptopow2_0(v) ((v) - 1)
#define uptopow2_1(v) (uptopow2_0(v) | uptopow2_0(v) >> 1)
#define uptopow2_2(v) (uptopow2_1(v) | uptopow2_1(v) >> 2)
#define uptopow2_3(v) (uptopow2_2(v) | uptopow2_2(v) >> 4)
#define uptopow2_4(v) (uptopow2_3(v) | uptopow2_3(v) >> 8)
#define uptopow2_5(v) (uptopow2_4(v) | uptopow2_4(v) >> 16)
#define uptopow2(v) (uptopow2_5(v) + 1) /* this is the one programmer uses */
Так, например, выражение вроде:
uptopow2(sizeof (struct foo))
будет приятно сводить к константе.
Я пытаюсь получить ближайшую более низкую степень 2 и сделал эту функцию. Пусть это поможет вам. Просто умножьте ближайший младший номер на 2, чтобы получить ближайшую верхнюю степень 2
int nearest_upper_power(int number){
int temp=number;
while((number&(number-1))!=0){
temp<<=1;
number&=temp;
}
//Here number is closest lower power
number*=2;
return number;
}
Если вам нужен однострочный шаблон. Вот
int nxt_po2(int n) { return 1 + (n|=(n|=(n|=(n|=(n|=(n-=1)>>1)>>2)>>4)>>8)>>16); }
или
int nxt_po2(int n) { return 1 + (n|=(n|=(n|=(n|=(n|=(n-=1)>>(1<<0))>>(1<<1))>>(1<<2))>>(1<<3))>>(1<<4)); }
Компилятор g++ предоставляет встроенную функцию __builtin_clz, которая считает ведущие нули:
Итак, мы могли сделать:
int nextPowerOfTwo(unsigned int x) {
return 1 << sizeof(x)*8 - __builtin_clz(x);
}
int main () {
std::cout << nextPowerOfTwo(7) << std::endl;
std::cout << nextPowerOfTwo(31) << std::endl;
std::cout << nextPowerOfTwo(33) << std::endl;
std::cout << nextPowerOfTwo(8) << std::endl;
std::cout << nextPowerOfTwo(91) << std::endl;
return 0;
}
Полученные результаты:
8
32
64
16
128
Но учтите, что для
x == 0,
__builtin_clz возврат не определен.
Адаптированный ответ Пола Диксона на Excel, это работает отлично.
=POWER(2,CEILING.MATH(LOG(A1)/LOG(2)))
Преобразуйте его в число с плавающей запятой, а затем используйте.hex(), который показывает нормализованное представление IEEE.
>>> float(789).hex()
'0x1.8a80000000000p+9'
Затем просто извлеките показатель степени и добавьте 1.
>>> int(float(789).hex().split('p+')[1]) + 1
10
И возвести 2 в эту степень.
>>> 2 ** (int(float(789).hex().split('p+')[1]) + 1)
1024
import sys
def is_power2(x):
return x > 0 and ((x & (x - 1)) == 0)
def find_nearest_power2(x):
if x <= 0:
raise ValueError("invalid input")
if is_power2(x):
return x
else:
bits = get_bits(x)
upper = 1 << (bits)
lower = 1 << (bits - 1)
mid = (upper + lower) // 2
if (x - mid) > 0:
return upper
else:
return lower
def get_bits(x):
"""return number of bits in binary representation"""
if x < 0:
raise ValueError("invalid input: input should be positive integer")
count = 0
while (x != 0):
try:
x = x >> 1
except TypeError as error:
print(error, "input should be of type integer")
sys.exit(1)
count += 1
return count
from math import ceil, log2
pot_ceil = lambda N: 0x1 << ceil(log2(N))
Тестовое задание:
for i in range(10):
print(i, pot_ceil(i))
Выход:
1 1
2 2
3 4
4 4
5 8
6 8
7 8
8 8
9 16
10 16