Умножение матриц: Штрассен против Стандарта
Я пытался реализовать алгоритм Штрассена для умножения матриц с помощью C++, но результат оказался не таким, как я ожидал. Как вы можете видеть, strassen всегда занимает больше времени, чем стандартная реализация, и только с измерением от степени 2 быстрее, чем стандартная реализация. Что пошло не так? 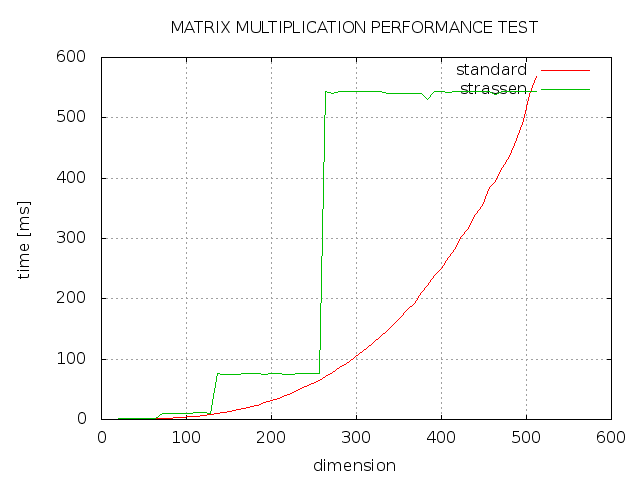
matrix mult_strassen(matrix a, matrix b) {
if (a.dim() <= cut)
return mult_std(a, b);
matrix a11 = get_part(0, 0, a);
matrix a12 = get_part(0, 1, a);
matrix a21 = get_part(1, 0, a);
matrix a22 = get_part(1, 1, a);
matrix b11 = get_part(0, 0, b);
matrix b12 = get_part(0, 1, b);
matrix b21 = get_part(1, 0, b);
matrix b22 = get_part(1, 1, b);
matrix m1 = mult_strassen(a11 + a22, b11 + b22);
matrix m2 = mult_strassen(a21 + a22, b11);
matrix m3 = mult_strassen(a11, b12 - b22);
matrix m4 = mult_strassen(a22, b21 - b11);
matrix m5 = mult_strassen(a11 + a12, b22);
matrix m6 = mult_strassen(a21 - a11, b11 + b12);
matrix m7 = mult_strassen(a12 - a22, b21 + b22);
matrix c(a.dim(), false, true);
set_part(0, 0, &c, m1 + m4 - m5 + m7);
set_part(0, 1, &c, m3 + m5);
set_part(1, 0, &c, m2 + m4);
set_part(1, 1, &c, m1 - m2 + m3 + m6);
return c;
}
ПРОГРАММА
matrix.h http://pastebin.com/TYFYCTY7
matrix.cpp http://pastebin.com/wYADLJ8Y
main.cpp http://pastebin.com/48BSqGJr
g++ main.cpp matrix.cpp -o matrix -O3,
5 ответов
Некоторые мысли:
- Оптимизировали ли вы это, чтобы учесть, что не степенная матрица двух размеров заполнена нулями? Я думаю, что алгоритм предполагает, что вы не удосуживаетесь умножать эти термины. Вот почему вы получаете плоские области, где время работы постоянно от 2^n до 2^(n+1)-1. Не умножая термины, которые, как вы знаете, равны нулю, вы сможете улучшить эти области. Или, возможно, Штрассен предназначен только для работы с матрицами размером 2^n.
- Считайте, что "большая" матрица произвольна, и алгоритм лишь немного лучше, чем в простом случае, O(N^3) против O(N^2.8). Вы можете не увидеть ощутимый выигрыш, пока не попробуете большие матрицы. Например, я провел моделирование методом конечных элементов, в котором матрицы размером 10000x100000 считались "маленькими". По вашему графику это трудно понять, но похоже, что случай 511 может быть быстрее в случае Штассена.
- Попробуйте тестирование с различными уровнями оптимизации, в том числе без оптимизации.
- Этот алгоритм, кажется, предполагает, что умножения намного дороже, чем сложения. Это было верно 40 лет назад, когда он был впервые разработан, но я верю, что в более современных процессорах разница между сложением и умножением стала меньше. Это может снизить эффективность алгоритма, который, по-видимому, уменьшает умножения, но увеличивает сложения.
- Вы смотрели на некоторые другие реализации Strassen там для идей? Попробуйте сравнить известную хорошую реализацию, чтобы точно узнать, насколько быстрее вы можете получить.
Большой O Штрассена равен O(N ^ log 7) по сравнению с O(N ^ 3) регулярным, то есть log 7 base 2, который немного меньше 3.
Это количество умножений, которое вам нужно сделать.
Предполагается, что ничего другого у вас нет, а также должно быть "быстрее" только потому, что N становится достаточно большим, чего, вероятно, нет у вас.
Большая часть вашей реализации создает множество подматриц, и я предполагаю, что способ их хранения заключается в том, что вам приходится выделять память и копировать каждый раз, когда вы делаете это. Наличие какой-либо матрицы "срезов" и матрицы логического транспонирования, если вы можете, поможет вам оптимизировать то, что, вероятно, является самой медленной частью вашего процесса.
Хорошо, я не эксперт в этой области, но здесь могут быть другие проблемы, кроме скорости обработки. Во-первых, метод strassen использует больше стека и имеет больше вызовов функций, которые добавляют движение памяти. У вас есть определенное наказание, чем больше ваш стек, так как он должен запрашивать большие кадры из ОС. Плюс вы используете динамическое распределение, это тоже проблема.
Попробуйте использовать матричный класс фиксированного размера (с параметром шаблона)? Это, по крайней мере, решит проблему распределения.
Примечание: я не уверен, что событие правильно работает с вашим кодом. Ваш матричный класс использует указатели, но не имеет конструктора копирования или оператора присваивания. Вы также теряете память в конце, так как у вас нет деструктора...
Я на самом деле шокирован тем, насколько быстрее моя реализация умножения Stassen:
http://ezekiel.vancouver.wsu.edu/~cs330/lectures/linear_algebra/mm/mm.c
Я получаю почти 16-кратное ускорение на моей машине, когда n=1024. Единственный способ объяснить такое ускорение - это то, что мой алгоритм более кеш-ориентирован, то есть он фокусируется на небольших фрагментах матриц и, следовательно, данные более локализованы.
Издержки в вашей реализации C++, вероятно, слишком высоки - компилятор генерирует больше временных значений, чем то, что действительно необходимо. Моя реализация пытается минимизировать это путем повторного использования памяти, когда это возможно.
Длинный выстрел, но считаете ли вы, что стандартное умножение может быть оптимизировано компилятором? Не могли бы вы отключить оптимизацию?