Эмпирический размер эффекта квантильного сравнения

Question

Я пытаюсь воссоздать следующий интеграл с эмпирическими данными:

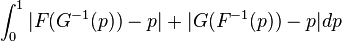
где F, G - cdfs, а их инверсии - квантильные функции.

Вот мой код:

def eqces(u,v):
    import numpy as np
    import statsmodels.api as sm
    from scipy.stats.mstats import mquantiles

    ecdfu = sm.distributions.ECDF(u)
    ecdfv = sm.distributions.ECDF(v)
    p = np.concatenate([ecdfu.y, ecdfv.y])
    p = np.unique(p) 
    p.sort()

    qfu = mquantiles(u, p)
    qfv = mquantiles(v, p)

    uvinv = ecdfu(qfv)
    vuinv = ecdfv(qfu)

    result = abs(uvinv - p) + abs(vuinv - p)
    return np.dot(result, np.ones(p.size))

С этим я бы ожидал, что eqces(u,u) = 0 за u = np.random.uniform(0,1,50) но это, как правило, не так. Может кто-нибудь сказать, если я делаю что-то не так или предложить альтернативы?

Edit

Этот код, кажется, лучше работает с некоторыми аналитическими результатами:

def eqces(u,v): 
    ecdfu = sm.distributions.ECDF(u)
    ecdfv = sm.distributions.ECDF(v)

    p = np.concatenate([ecdfu.y, ecdfv.y])
    X = np.concatenate([ecdfu.x, ecdfv.x])

    return 2*np.dot(np.abs(ecdfu(X)-p)+np.abs(ecdfv(X)-p), np.ones(p.size))/p.size

Answer 1

Я думаю, что ECDF а также mquantiles не используйте одни и те же позиции

mquantiles имеет дополнительные ключевые слова alphap=0.4, betap=0.4,

p а также uvinv не будет в оба конца в этом случае.

Однако в большой выборке разница должна быть небольшой.

scipy.stats.ks_2samp делает нечто подобное, но работает напрямую с NumPy без вспомогательных функций.

Кстати: есть ли у этого измерения расстояния между двумя распределениями имя?