Добавить экспоненциальную функцию с заданным средним значением и перехватить на графике cdf

Question

Учитывая следующие случайные данные:

set.seed(123456)
# generate random normal data
x <- rnorm(100, mean = 20, sd = 5)
weights <- 1:100
df1 <- data.frame(x, weights)

#
library(ggplot2)
ggplot(df1, aes(x)) + stat_ecdf()

Мы можем создать общий кумулятивный график распределения.

Но я хочу сравнить свою кривую с данными, использованными 20 лет назад. Из этой статьи я знаю только то, что данные "лучше всего моделируются смещенным экспоненциальным распределением с перехватом x 1,1 и средним значением 18"

Как я могу добавить такую ​​функцию на свой график?

+ stat_function(fun=dexp, geom = "line", size=2, col="red", args = (mean=18.1))

но я не уверен, как бороться со сдвигом (х перехват)

Answer 1

Я думаю, что сценарии, подобные этому, лучше всего обрабатывать, function первый за пределами ggplot вызов.

dexp не принимает параметр mean но использует rate вместо того, что так же, как lambda, Это означает, что вы хотите rate = 1/18.1 основанный на свойствах экспоненциальных распределений. Кроме того, я не думаю, dexp имеет большой смысл здесь, так как он показывает плотность, и я думаю, что вы действительно хотите, чтобы вероятность с pexp,

ваш код может выглядеть примерно так:

library(ggplot2)
test <- function(x) {pexp(x, rate = 1/18.1)}
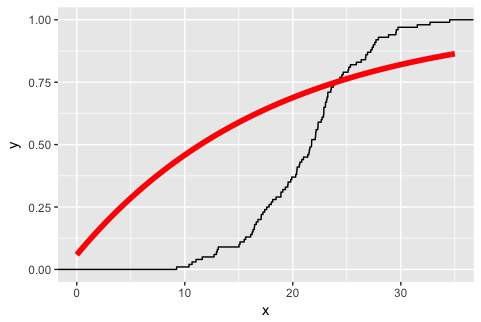
ggplot(df1, aes(x)) + stat_ecdf() +
    stat_function(fun=test, size=2, col="red")

Вы могли бы сдвинуть pexp дистрибутивы делают это:

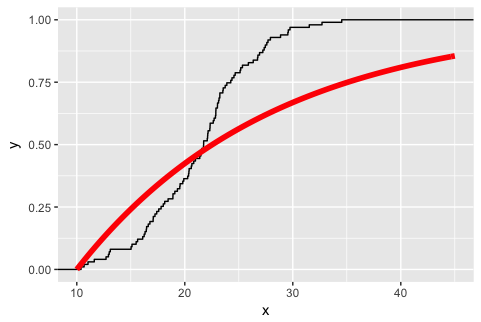
test <- function(x) {pexp(x-10, rate = 1/18.1)}
ggplot(df1, aes(x)) + stat_ecdf() +
    stat_function(fun=test, size=2, col="red") +
    xlim(10,45)

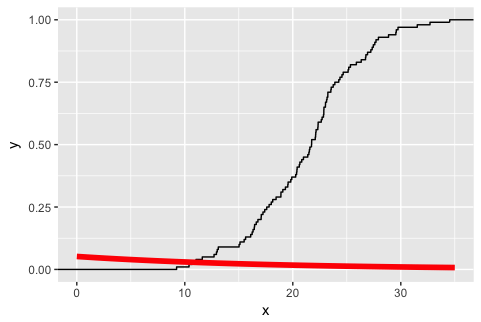
просто для удовольствия это то, что с помощью dexp производит:

Answer 2

Я не совсем уверен, понимаю ли я понятие среднего для экспоненциальной функции. Однако, как правило, когда вы передаете функцию в качестве аргумента, который fun=dexp в вашем случае вы можете передавать свои собственные модифицированные функции в виде: fun = function(x) dexp(x)+1.1, например. Возможно, экспериментируя с этой функцией, вы получите решение.