Числовые задачи точности в R?

Question

У меня проблема со следующей функцией в R:

test <- function(alpha, beta, n){
  result <- exp(lgamma(alpha) + lgamma(n + beta) - lgamma(alpha + beta + n) - (lgamma(alpha) + lgamma(beta) - lgamma(alpha + beta)))
  return(result)
}

Теперь, если вы вставите следующие значения:

betabinom(-0.03292708, -0.3336882, 10)

Это должно потерпеть неудачу и привести к NaN, Это потому, что если мы реализуем точную функцию в Excel, мы получим результат, который не является числом. Реализация в Excel проста, для J32 это ячейка для alphaК32 beta и L32 для N, Реализация полученной ячейки приведена ниже:

=EXP(GAMMALN(J32)+GAMMALN(L32+K32)-GAMMALN(J32+K32+L32)-(GAMMALN(J32)+GAMMALN(K32)-GAMMALN(J32+K32)))

Так что это, кажется, дает правильный ответ, потому что функция определена только для альфа и бета больше нуля и n больше или равно нулю. Поэтому мне интересно, что здесь происходит? Я также попробовал пакет Rmpf, чтобы увеличить числовую точность, но это, похоже, ничего не делает.

Спасибо

Answer 1

tl; dr log (gamma (x)) определяется более широко, чем вы думаете, или чем думает Excel. Если вы хотите, чтобы ваша функция не принимала отрицательные значения alpha а также beta или вернуть NaN, просто протестируйте вручную и верните соответствующие значения (if (alpha<0 || beta<0) return(NaN)).

Это не проблема числовой точности, это проблема определения. Гамма-функция определена для отрицательных реальных значений: ?lgamma говорит:

Гамма-функция определяется (Абрамовиц и Стегун, раздел 6.1.1, стр. 255).

Гамма (x) = интеграл_0^Inf t^(x-1) exp(-t) dt

для всех вещественных "x", кроме нулевых и отрицательных целых чисел (когда возвращается "NaN").

Кроме того, ссылаясь на lgamma...

... и натуральный логарифм абсолютного значения гамма-функции...

(акцент в оригинале)

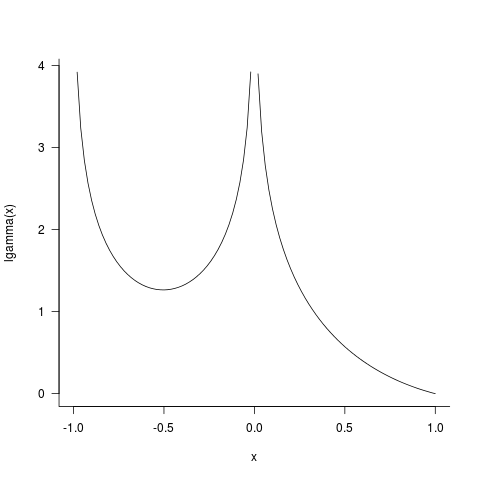
curve(lgamma(x),-1,1)

gamma(-0.1)          ## -10.68629
log(gamma(-0.1)+0i)  ## 2.368961+3.141593i
log(abs(gamma(-0.1)) ## 2.368961
lgamma(-0.1)         ## 2.368961

Вольфрам Альфа согласен со вторым расчетом.