Минимизация DFA
У меня есть вопрос о минимизации DFA. Поэтому я использовал очень хорошо известные методы для преобразования регулярного выражения в NFA, а затем для создания DFA из него, используя алгоритм goto / closure. Теперь вопрос, как мне минимизировать это? Я смотрел лекции об этом здесь: http://www.youtube.com/watch?v=T9Z66NF5YRk и до сих пор не могу понять суть. Что такое минимизация DFA? Это просто объединение ИДЕНТИЧНЫХ состояний (состояний, которые переходят в одни и те же состояния на одних и тех же символах) или что-то другое?
Итак, я начал со следующей грамматики:
%digit = '0'..'9'
%letter = 'a'..'z' | 'A'..'Z'
%exponent = ("e" | "E") ("+" | "-")? digit+
T_INT = digit+
T_FLOAT = T_INT exponent
T_IDENTIFIER = (letter | "$" | "_") (letter | "$" | "_" | digit)*
и в итоге получим следующий DFA (представленный как JSON):
{
"START": [{
"type": "range",
"from": 36,
"to": 36,
"shift": "1"
}, {
"type": "range",
"from": 48,
"to": 57,
"shift": "2"
}, {
"type": "range",
"from": 65,
"to": 90,
"shift": "1"
}, {
"type": "range",
"from": 95,
"to": 95,
"shift": "1"
}, {
"type": "range",
"from": 97,
"to": 122,
"shift": "1"
}],
"1": [{
"type": "range",
"from": 36,
"to": 36,
"shift": "1"
}, {
"type": "range",
"from": 48,
"to": 57,
"shift": "1"
}, {
"type": "range",
"from": 65,
"to": 90,
"shift": "1"
}, {
"type": "range",
"from": 95,
"to": 95,
"shift": "1"
}, {
"type": "range",
"from": 97,
"to": 122,
"shift": "1"
}, {
"shift": ["t_identifier"]
}],
"2": [{
"type": "range",
"from": 48,
"to": 57,
"shift": "2"
}, {
"type": "range",
"from": 69,
"to": 69,
"shift": "3"
}, {
"type": "range",
"from": 101,
"to": 101,
"shift": "3"
}, {
"shift": ["t_int"]
}],
"3": [{
"type": "range",
"from": 43,
"to": 43,
"shift": "5"
}, {
"type": "range",
"from": 45,
"to": 45,
"shift": "5"
}, {
"type": "range",
"from": 48,
"to": 57,
"shift": "4"
}],
"4": [{
"type": "range",
"from": 48,
"to": 57,
"shift": "4"
}, {
"shift": ["t_float"]
}],
"5": [{
"type": "range",
"from": 48,
"to": 57,
"shift": "4"
}]
}
Так как мне минимизировать это?
ОБНОВИТЬ:
Итак, вот мой алгоритм. Учитывая следующее DFA:
{
0: [{
from: 97,
to: 97,
shift: 1
}],
1: [{
from: 97,
to: 97,
shift: 3
}, {
from: 98,
to: 98,
shift: 2
}],
2: [{
from: 98,
to: 98,
shift: 4
}],
3: [{
from: 97,
to: 97,
shift: 3
}, {
from: 98,
to: 98,
shift: 4
}],
4: [{
from: 98,
to: 98,
shift: 4
}]
}
Вот что я делаю, чтобы минимизировать это:
Для каждого состояния (в моем примере это 0, 1, 2, 3, 4) получите уникальный хеш, который идентифицирует такое состояние (например, для state0 это будет: от =97, до =97,shift=1, для state1 это будет: от = 97 до =97, смещение =3 и с =98, до =98, смещение =2 и т. д.)
Сравните полученные хеши, и если мы найдем два одинаковых, то объединяем их. В моем примере хэш state2 будет: from=98&shift=4&to=98, а хэш state4 будет: from=98&shift=4&to=98, они одинаковы, поэтому мы можем объединить их в новое состояние5, после чего DFA будет выглядеть так:
{ 0: [{ from: 97, to: 97, shift: 1 }], 1: [{ from: 97, to: 97, shift: 3 }, { from: 98, to: 98, shift: 5 }], 3: [{ from: 97, to: 97, shift: 3 }, { from: 98, to: 98, shift: 5 }], 5: [{ from: 98, to: 98, shift: 5 }]}
Продолжайте до тех пор, пока мы не получим никаких изменений, поэтому следующий шаг (объединение состояний 1 и 3) преобразует DFA в следующую форму:
{ 0: [{ from: 97, to: 97, shift: 6 }], 6: [{ from: 97, to: 97, shift: 6 }, { from: 98, to: 98, shift: 5 }], 5: [{ from: 98, to: 98, shift: 5 }]}
Больше нет идентичных состояний, это значит, что мы закончили.
ВТОРОЕ ОБНОВЛЕНИЕ:
Итак, учитывая следующее регулярное выражение: 'a' ('ce')* ('d' | 'xa' | 'AFe')+ | 'b' ('ce')* ('d' | 'xa' | 'AFe')+ 'ce'+ У меня есть следующее DFA (START -> начальное состояние, ["accept"] -> так, чтобы скажем переход в принимающее состояние)
{
"START": [{
"type": "range",
"from": 98,
"to": 98,
"shift": "1.2"
}, {
"type": "range",
"from": 97,
"to": 97,
"shift": "17.18"
}],
"1.2": [{
"type": "range",
"from": 120,
"to": 120,
"shift": "10"
}, {
"type": "range",
"from": 100,
"to": 100,
"shift": "6.7"
}, {
"type": "range",
"from": 65,
"to": 65,
"shift": "8"
}, {
"type": "range",
"from": 99,
"to": 99,
"shift": "4"
}],
"10": [{
"type": "range",
"from": 97,
"to": 97,
"shift": "6.7"
}],
"6.7": [{
"type": "range",
"from": 99,
"to": 99,
"shift": "15"
}, {
"type": "range",
"from": 120,
"to": 120,
"shift": "13"
}, {
"type": "range",
"from": 100,
"to": 100,
"shift": "6.7"
}, {
"type": "range",
"from": 65,
"to": 65,
"shift": "11"
}],
"15": [{
"type": "range",
"from": 101,
"to": 101,
"shift": "14.accept"
}],
"14.accept": [{
"type": "range",
"from": 99,
"to": 99,
"shift": "16"
}, {
"shift": ["accept"]
}],
"16": [{
"type": "range",
"from": 101,
"to": 101,
"shift": "14.accept"
}],
"13": [{
"type": "range",
"from": 97,
"to": 97,
"shift": "6.7"
}],
"11": [{
"type": "range",
"from": 70,
"to": 70,
"shift": "12"
}],
"12": [{
"type": "range",
"from": 101,
"to": 101,
"shift": "6.7"
}],
"8": [{
"type": "range",
"from": 70,
"to": 70,
"shift": "9"
}],
"9": [{
"type": "range",
"from": 101,
"to": 101,
"shift": "6.7"
}],
"4": [{
"type": "range",
"from": 101,
"to": 101,
"shift": "2.3"
}],
"2.3": [{
"type": "range",
"from": 120,
"to": 120,
"shift": "10"
}, {
"type": "range",
"from": 100,
"to": 100,
"shift": "6.7"
}, {
"type": "range",
"from": 65,
"to": 65,
"shift": "8"
}, {
"type": "range",
"from": 99,
"to": 99,
"shift": "5"
}],
"5": [{
"type": "range",
"from": 101,
"to": 101,
"shift": "2.3"
}],
"17.18": [{
"type": "range",
"from": 120,
"to": 120,
"shift": "25"
}, {
"type": "range",
"from": 100,
"to": 100,
"shift": "22.accept"
}, {
"type": "range",
"from": 65,
"to": 65,
"shift": "23"
}, {
"type": "range",
"from": 99,
"to": 99,
"shift": "20"
}],
"25": [{
"type": "range",
"from": 97,
"to": 97,
"shift": "22.accept"
}],
"22.accept": [{
"type": "range",
"from": 120,
"to": 120,
"shift": "28"
}, {
"type": "range",
"from": 100,
"to": 100,
"shift": "22.accept"
}, {
"type": "range",
"from": 65,
"to": 65,
"shift": "26"
}, {
"shift": ["accept"]
}],
"28": [{
"type": "range",
"from": 97,
"to": 97,
"shift": "22.accept"
}],
"26": [{
"type": "range",
"from": 70,
"to": 70,
"shift": "27"
}],
"27": [{
"type": "range",
"from": 101,
"to": 101,
"shift": "22.accept"
}],
"23": [{
"type": "range",
"from": 70,
"to": 70,
"shift": "24"
}],
"24": [{
"type": "range",
"from": 101,
"to": 101,
"shift": "22.accept"
}],
"20": [{
"type": "range",
"from": 101,
"to": 101,
"shift": "18.19"
}],
"18.19": [{
"type": "range",
"from": 120,
"to": 120,
"shift": "25"
}, {
"type": "range",
"from": 100,
"to": 100,
"shift": "22.accept"
}, {
"type": "range",
"from": 65,
"to": 65,
"shift": "23"
}, {
"type": "range",
"from": 99,
"to": 99,
"shift": "21"
}],
"21": [{
"type": "range",
"from": 101,
"to": 101,
"shift": "18.19"
}]
}
История такая же, как мне ее минимизировать? Если я буду следовать классическому алгоритму Хопкрофта со всей этой конструкцией таблицы, определяя неразличимые состояния, объединяя их вместе и так далее, то я получу DFA, содержащий 15 состояний (используйте этот инструмент: http://regexvisualizer.apphb.com/ с этим регулярным выражением a (ce)(d | xa | AFe) + | b (ce)(d | xa | AFe) + ce +, чтобы проверить это). Вот как выглядит DFA после минификации с помощью алгоритма Хопкрофта:
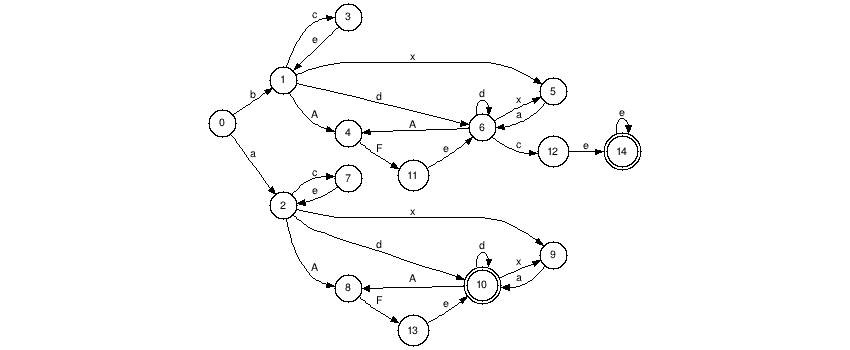
Алгоритм, который я придумал, после "переосмысления" алгоритма Хопкрофта создает DFA, меньший, чем тот, который вы видите выше (извините за качество изображения, мне пришлось перерисовывать его шаг за шагом, чтобы понять, почему он меньше):
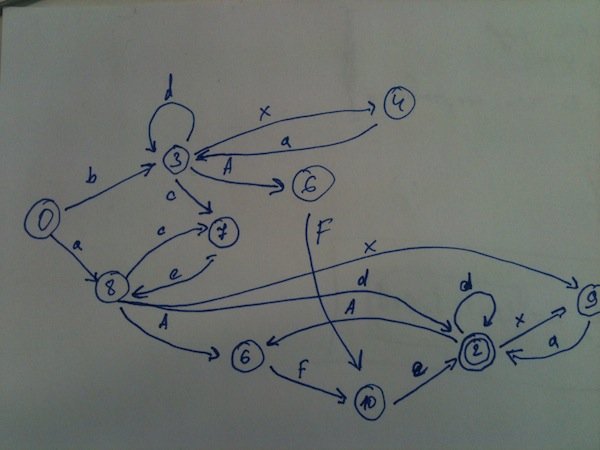
И вот как это работает, решение о "эквивалентности состояний" основывается на результате хеш-функции, которой присваивается состояние (например, "START"), строит короткие строки, которые могут быть построены из DFA, если мы начнем с этого состояния., Учитывая приведенное выше DFA и состояние START, мы можем построить следующие строки: 98->120, 98->100, 98->65, 98->99, 97->120, 97->100, 97->65, 97->99, поэтому пусть это будет результат хеш-функции для состояния START. Если мы запустим эту функцию для каждого состояния в DFA, мы увидим, что для некоторых состояний эта функция дает нам идентичные результаты ("1.2", "6.7", "2.3" И "10", "13" И "15", "16" И "11", "8", "26", "23" И "12", "9", "4", "5", "20", "21" И "17.18", "18.19"И"25", "28"И"27", "24"), поэтому все, что нам нужно сделать, это объединить эти состояния вместе.
Я вижу, что где-то не прав, но не понимаю, что не так с минимизированным DFA, созданным моим алгоритмом?
3 ответа
Предложенный вами алгоритм не выполняет полную минимизацию, поскольку он не обнаруживает сложные структуры, которые ведут себя одинаково. Чтобы понять это, посмотрите на этот DFA (нарисованный JFLAP):

Минимизация объединит q1 и q2, но изложенный алгоритм не удастся.
В отличие от этого, алгоритм Хопкрофта первоначально разделился бы так:
{q0, q1, q2}, {q3}
затем разбить первый набор, потому что q0 не имеет перехода к q3:
{q0}, {q1, q2}, {q3}
и не разделяться дальше, потому что q1 и q2 ведут себя одинаково.
Пусть ваш оригинальный DFA будет называться M1. Проще говоря, построение минимизированного DFA (назовите его M2) подразумевает преобразование его в DFA, который содержит минимальное количество состояний. Таким образом, число состояний в M2 будет меньше, чем число состояний в M1. Здесь важно отметить, что M1 и M2 должны быть эквивалентны, что означает, что они должны определять ТО ЖЕ регулярный язык. Создание минимизированного DFA включает не только поиск идентичных состояний, но и следующее:
Удаление "недостижимых" состояний:
Это включает в себя удаление состояний, которые недоступны из начального состояния DFA, для любой входной строки.Удаление "мертвых" или "ловушечных" состояний:
Это включает в себя удаление непринимающих состояний, которое заканчивается само по себе. Они также называются состояниями TRAP.Удаление "неотличимых" состояний:
Это включает в себя удаление состояний, которые нельзя отличить друг от друга для любой входной строки.
Есть также несколько популярных алгоритмов, используемых для минимизации DFA:
Возможно, стоит пройтись по этим алгоритмам!
Учитывая, что у вас есть код для определения NFA для DFA, простейшим решением минимизировать его является алгоритм Бжозовского. Вам нужно будет реализовать функцию для обратного NFA, но это довольно просто. (поменять местами переходы, поменять местами старт и принять состояния)
Как только у вас есть определительная и обратная функция, минимизация Бжозовского реализуется следующим образом:
minimize(nfa) = determinize(reverse(determinize(reverse(nfa))))
ИМХО, это очень элегантное решение