R: Экстремальное связывание случайных значений из Рунифа с семенем Мерсенна-Твистера
Мы сталкиваемся со странной ситуацией в нашем коде при использовании R runif и установка семян с set.seed с kind = NULL вариант (который разрешает, если я не ошибаюсь, kind = "default"; по умолчанию "Mersenne-Twister").
Мы устанавливаем начальное значение, используя (8 цифр) уникальные идентификаторы, сгенерированные восходящей системой, перед вызовом runif:
seeds = c(
"86548915", "86551615", "86566163", "86577411", "86584144",
"86584272", "86620568", "86724613", "86756002", "86768593", "86772411",
"86781516", "86794389", "86805854", "86814600", "86835092", "86874179",
"86876466", "86901193", "86987847", "86988080")
random_values = sapply(seeds, function(x) {
set.seed(x)
y = runif(1, 17, 26)
return(y)
})
Это дает значения, которые чрезвычайно сгруппированы вместе.
> summary(random_values)
Min. 1st Qu. Median Mean 3rd Qu. Max.
25.13 25.36 25.66 25.58 25.83 25.94
Это поведение runif уходит, когда мы используем kind = "Knuth-TAOCP-2002" и мы получаем значения, которые кажутся гораздо более равномерно распределенными.
random_values = sapply(seeds, function(x) {
set.seed(x, kind = "Knuth-TAOCP-2002")
y = runif(1, 17, 26)
return(y)
})
Выход опущен.
Самое интересное здесь то, что это не происходит в Windows - только в Ubuntu (sessionInfo выход для Ubuntu и Windows ниже).
Вывод Windows:
> seeds = c(
+ "86548915", "86551615", "86566163", "86577411", "86584144",
+ "86584272", "86620568", "86724613", "86756002", "86768593", "86772411",
+ "86781516", "86794389", "86805854", "86814600", "86835092", "86874179",
+ "86876466", "86901193", "86987847", "86988080")
>
> random_values = sapply(seeds, function(x) {
+ set.seed(x)
+ y = runif(1, 17, 26)
+ return(y)
+ })
>
> summary(random_values)
Min. 1st Qu. Median Mean 3rd Qu. Max.
17.32 20.14 23.00 22.17 24.07 25.90
Может кто-нибудь помочь понять, что происходит?
Ubuntu
R version 3.4.0 (2017-04-21)
Platform: x86_64-pc-linux-gnu (64-bit)
Running under: Ubuntu 16.04.2 LTS
Matrix products: default
BLAS: /usr/lib/libblas/libblas.so.3.6.0
LAPACK: /usr/lib/lapack/liblapack.so.3.6.0
locale:
[1] LC_CTYPE=en_US.UTF-8 LC_NUMERIC=C
[3] LC_TIME=en_US.UTF-8 LC_COLLATE=en_US.UTF-8
[5] LC_MONETARY=en_US.UTF-8 LC_MESSAGES=en_US.UTF-8
[7] LC_PAPER=en_US.UTF-8 LC_NAME=en_US.UTF-8
[9] LC_ADDRESS=en_US.UTF-8 LC_TELEPHONE=en_US.UTF-8
[11] LC_MEASUREMENT=en_US.UTF-8 LC_IDENTIFICATION=en_US.UTF-8
attached base packages:
[1] parallel stats graphics grDevices utils datasets methods base
other attached packages:
[1] RMySQL_0.10.8 DBI_0.6-1
[3] jsonlite_1.4 tidyjson_0.2.2
[5] optiRum_0.37.3 lubridate_1.6.0
[7] httr_1.2.1 gdata_2.18.0
[9] XLConnect_0.2-12 XLConnectJars_0.2-12
[11] data.table_1.10.4 stringr_1.2.0
[13] readxl_1.0.0 xlsx_0.5.7
[15] xlsxjars_0.6.1 rJava_0.9-8
[17] sqldf_0.4-10 RSQLite_1.1-2
[19] gsubfn_0.6-6 proto_1.0.0
[21] dplyr_0.5.0 purrr_0.2.4
[23] readr_1.1.1 tidyr_0.6.3
[25] tibble_1.3.0 tidyverse_1.1.1
[27] rBayesianOptimization_1.1.0 xgboost_0.6-4
[29] MLmetrics_1.1.1 caret_6.0-76
[31] ROCR_1.0-7 gplots_3.0.1
[33] effects_3.1-2 pROC_1.10.0
[35] pscl_1.4.9 lattice_0.20-35
[37] MASS_7.3-47 ggplot2_2.2.1
loaded via a namespace (and not attached):
[1] splines_3.4.0 foreach_1.4.3 AUC_0.3.0 modelr_0.1.0
[5] gtools_3.5.0 assertthat_0.2.0 stats4_3.4.0 cellranger_1.1.0
[9] quantreg_5.33 chron_2.3-50 digest_0.6.10 rvest_0.3.2
[13] minqa_1.2.4 colorspace_1.3-2 Matrix_1.2-10 plyr_1.8.4
[17] psych_1.7.3.21 XML_3.98-1.7 broom_0.4.2 SparseM_1.77
[21] haven_1.0.0 scales_0.4.1 lme4_1.1-13 MatrixModels_0.4-1
[25] mgcv_1.8-17 car_2.1-5 nnet_7.3-12 lazyeval_0.2.0
[29] pbkrtest_0.4-7 mnormt_1.5-5 magrittr_1.5 memoise_1.0.0
[33] nlme_3.1-131 forcats_0.2.0 xml2_1.1.1 foreign_0.8-69
[37] tools_3.4.0 hms_0.3 munsell_0.4.3 compiler_3.4.0
[41] caTools_1.17.1 rlang_0.1.1 grid_3.4.0 nloptr_1.0.4
[45] iterators_1.0.8 bitops_1.0-6 tcltk_3.4.0 gtable_0.2.0
[49] ModelMetrics_1.1.0 codetools_0.2-15 reshape2_1.4.2 R6_2.2.0
[53] knitr_1.15.1 KernSmooth_2.23-15 stringi_1.1.5 Rcpp_0.12.11
Windows
> sessionInfo()
R version 3.3.2 (2016-10-31)
Platform: x86_64-w64-mingw32/x64 (64-bit)
Running under: Windows >= 8 x64 (build 9200)
locale:
[1] LC_COLLATE=English_India.1252 LC_CTYPE=English_India.1252 LC_MONETARY=English_India.1252
[4] LC_NUMERIC=C LC_TIME=English_India.1252
attached base packages:
[1] graphics grDevices utils datasets grid stats methods base
other attached packages:
[1] bindrcpp_0.2 h2o_3.14.0.3 ggrepel_0.6.5 eulerr_1.1.0 VennDiagram_1.6.17
[6] futile.logger_1.4.3 scales_0.4.1 FinCal_0.6.3 xml2_1.0.0 httr_1.3.0
[11] wesanderson_0.3.2 wordcloud_2.5 RColorBrewer_1.1-2 htmltools_0.3.6 urltools_1.6.0
[16] timevis_0.4 dtplyr_0.0.1 magrittr_1.5 shiny_1.0.5 RODBC_1.3-14
[21] zoo_1.8-0 sqldf_0.4-10 RSQLite_1.1-2 gsubfn_0.6-6 proto_1.0.0
[26] gdata_2.17.0 stringr_1.2.0 XLConnect_0.2-12 XLConnectJars_0.2-12 data.table_1.10.4
[31] xlsx_0.5.7 xlsxjars_0.6.1 rJava_0.9-8 readxl_0.1.1 googlesheets_0.2.1
[36] jsonlite_1.5 tidyjson_0.2.1 RMySQL_0.10.9 RPostgreSQL_0.4-1 DBI_0.5-1
[41] dplyr_0.7.2 purrr_0.2.3 readr_1.1.1 tidyr_0.7.0 tibble_1.3.3
[46] ggplot2_2.2.0 tidyverse_1.0.0 lubridate_1.6.0
loaded via a namespace (and not attached):
[1] gtools_3.5.0 assertthat_0.2.0 triebeard_0.3.0 cellranger_1.1.0 yaml_2.1.14
[6] slam_0.1-40 lattice_0.20-34 glue_1.1.1 chron_2.3-48 digest_0.6.12.1
[11] colorspace_1.3-1 httpuv_1.3.5 plyr_1.8.4 pkgconfig_2.0.1 xtable_1.8-2
[16] lazyeval_0.2.0 mime_0.5 memoise_1.0.0 tools_3.3.2 hms_0.3
[21] munsell_0.4.3 lambda.r_1.1.9 rlang_0.1.1 RCurl_1.95-4.8 labeling_0.3
[26] bitops_1.0-6 tcltk_3.3.2 gtable_0.2.0 reshape2_1.4.2 R6_2.2.0
[31] bindr_0.1 futile.options_1.0.0 stringi_1.1.2 Rcpp_0.12.12.1
3 ответа
ПРИМЕЧАНИЕ. В этом ответе обобщены элементы обсуждения этого вопроса, которое состоялось в списке рассылки R-devel. Я просто попытался уловить и обобщить идеи, изначально сформулированные там.
Несмотря на ваши заверения, что эти числа не являются специально сконструированными краевыми случаями, они кажутся именно такими. Вот исходная последовательность плюс код для проверки распределения произведенных значений:
seeds = c(
86548915, 86551615, 86566163, 86577411, 86584144, 86584272,
86620568, 86724613, 86756002, 86768593, 86772411, 86781516,
86794389, 86805854, 86814600, 86835092, 86874179, 86876466,
86901193, 86987847, 86988080)
checkit <- function(seeds) {
sapply(seeds, function(x) {
set.seed(x)
y = runif(1, 17, 26)
return(y)
})}
Исходная последовательность демонстрирует удивительно небольшое изменение, как отмечалось:
summary(checkit(seeds+0))
## Min. 1st Qu. Median Mean 3rd Qu. Max.
##25.13 25.36 25.66 25.58 25.83 25.94
В оригинальной последовательности, похоже, есть что-то особенное, поскольку минимальные модификации не дают такого же удивительного результата:
summary(checkit(seeds+1))
## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 17.18 19.65 22.75 22.02 24.37 25.79
summary(checkit(seeds-1))
## Min. 1st Qu. Median Mean 3rd Qu. Max.
##17.15 18.44 19.92 20.77 22.97 25.95
Из всех семян в диапазоне, охватываемом исходной последовательностью, ожидаемое число дает значения в наблюдаемом диапазоне:
possible.seeds <- min(seeds):max(seeds)
s25 <- Filter(function(s){
set.seed(s)
x <- runif(1,17,26)
x > 25.12 & x < 25.95},
possible.seeds)
length(s25)/length(possible.seeds)
##[1] 0.09175801
И все же, все значения в исходной последовательности находятся в этом подмножестве (конечно, мы уже знали это...).
table(seeds %in% s25)
##TRUE
## 21
Все это указывает на вероятную возможность того, что исходная последовательность была (возможно, непреднамеренно) специально построенным краевым случаем.
В качестве еще одного доказательства того, что ваша последовательность представляет собой крайний случай, вы можете сфокусироваться на диапазоне предположительно случайных значений. 17 и 26 немного отвлекают. Повторение вашего эксперимента с равномерным на 0 и 1 приводит к чему-то одинаково маловероятному:
f <- function(x) {
set.seed(x)
runif(1)
}
check_range <-function(seeds){
vals <- sapply(seeds,f)
max(vals)-min(vals)
}
Когда бегите против ваших семян:
> check_range(seeds)
[1] 0.09026112
Разумная модель для check_range(seeds) при запуске на 21 случайном семени это выборка случайной выборки размером 21 U(0,1), Его теоретическая плотность определяется как:
f <- function(x){420*x^19*(1-x)}
Мы можем использовать это для вычисления вероятности наблюдения диапазона 0,09 или меньше:
> integrate(f,0,0.09)
2.334272e-20 with absolute error < 2.6e-34
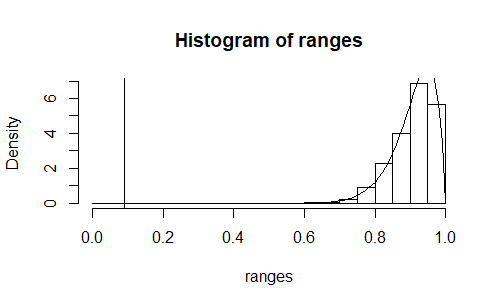
В качестве проверки того, что при посеве Мерсенна Твистера целесообразно смоделировать диапазон выборки, вы можете выполнить следующий эксперимент:
ranges <- replicate(1000,check_range(sample(8548915:86988080,21)))
x <- seq(0,1,0.01)
y <- f(x)
hist(ranges,freq = FALSE,xlim =c(0,1))
points(x,y,type = "l")
abline(v=0.09)
Выход:
Гистограмма плотности достаточно хорошо следует теоретической плотности. Набор из 21 семечки из вашего вопроса представляет собой экстремальный выброс. Очень маловероятно, что это происходит из-за случайности, а также из-за какого-то существенного недостатка в Twister Mersenne. Наиболее вероятным объяснением является то, что сам Мерсенн Твистер участвовал в создании этих 21 значений (но, конечно, не наивным способом простого использования sample() нарисовать 21 значение).
Когда вы используете Mersenne Twister с одним начальным числом, разумно предположить, что сгенерированные значения примерно независимы и одинаково распределены. К сожалению, нет никаких гарантий относительно сгенерированных значений из двух потоков, запущенных в разных семенах. Смотрите, например, эту ветку SC.
В вашей ситуации я бы порекомендовал либо использовать одну из стратегий выбора начальных значений, предложенных в потоке SC, либо переключиться на PRNG с лучшими гарантиями параллельных потоков. Одним из вариантов является генератор R'StStreams от L'Ecuyer:
set.seed(0, kind = "L'Ecuyer-CMRG")
Даже с этим PRNG, я не знаю, все еще ли это, что вы можете заполнить PRNG произвольными семенами и получить примерно независимые потоки.
Что касается различия между Ubuntu и Windows, возможно, что одна из этих систем использует 32-разрядный генератор, а другая - 64-разрядную.