Когда и почему кроссовер полезен в дифференциальной эволюции?

Question

Я реализовал алгоритм дифференциальной эволюции для побочного проекта, который я делал. Поскольку шаг кроссовера, казалось, включал в себя множество вариантов выбора параметров (например, вероятности кроссовера), я решил пропустить его и просто использовать мутацию. Метод, казалось, работал нормально, но я не уверен, смогу ли я получить лучшую производительность, если бы я ввел кроссовер.

Главный вопрос: какова мотивация внедрения кроссовера для дифференциальной эволюции? Можете ли вы привести игрушечный пример, где внедрение кроссовера превосходит чистую мутацию?

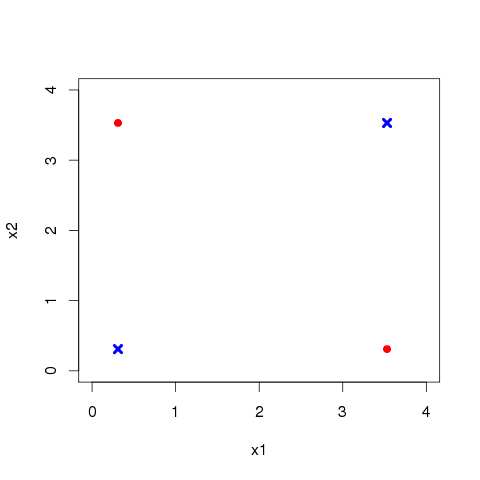
Моя интуиция заключается в том, что кроссовер будет производить что-то вроде следующего в двух измерениях. Скажем, у нас есть два родительских вектора (красный). Равномерный кроссовер может создать новый пробный вектор в одной из синих точек.

Я не уверен, почему такого рода исследования могут быть полезными. На самом деле, кажется, что это может ухудшить производительность, если решения для фитнеса будут следовать некоторой линейной тенденции. На рисунке ниже предположим, что красные точки - это текущая популяция, а оптимальное решение - в правом нижнем углу. Население путешествует по долине так, что верхний правый и нижний левый углы дают плохие решения. Верхний левый угол дает "хорошо", но неоптимальные решения. Обратите внимание, как равномерный кроссовер производит испытания (синим цветом), которые ортогональны направлению улучшения. Я использовал вероятность перехода 1 и пренебрегли мутацией, чтобы проиллюстрировать свою точку зрения (см. Код). Я полагаю, что такая ситуация может возникать довольно часто в задачах оптимизации, но может что-то недопонимать.

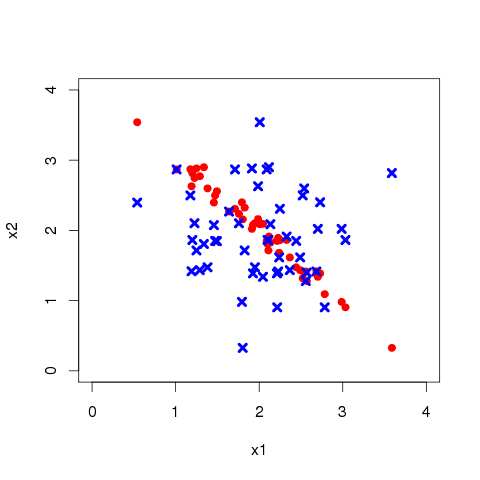
Примечание. В приведенном выше примере я неявно предполагаю, что популяция была случайным образом (равномерно) инициализирована по всему этому пространству и начала сходиться к правильному решению в центральной долине (слева направо и снизу справа).

Этот игрушечный пример выпуклый, и поэтому дифференциальная эволюция даже не будет подходящей техникой. Однако, если этот мотив был встроен в мультимодальный фитнес-ландшафт, кажется, что кроссовер может быть вредным. Хотя кроссовер поддерживает исследования, которые могут быть полезными, я не уверен, почему кто-то выбрал бы исследование в этом конкретном направлении.

R код для примера выше:

N = 50

x1 <- rnorm(N,mean=2,sd=0.5)
x2 <- -x1+4+rnorm(N,mean=0,sd=0.1)
plot(x1,x2,pch=21,col='red',bg='red',ylim=c(0,4),xlim=c(0,4))

x1_cx = list(rep(0, 50))
x2_cx = list(rep(0, 50))
for (i in 0:N) {
  x1_cx[i] <- x1[i]
  x2_cx[i] <- x2[sample(1:N,1)]
}

points(x1_cx,x2_cx,pch=4,col='blue',lwd=4)

Дополнительный вопрос: Если в определенных ситуациях выгодно пересечение, существует ли разумный подход к: а) определению того, выиграет ли ваша конкретная проблема от пересечения, и б) как настроить параметры пересечения для оптимизации алгоритма?

Смежный вопрос о переполнении стека (я ищу что-то более конкретное, например, с игрушечным примером): какова важность перехода в алгоритме дифференциальной эволюции?

Подобный вопрос, но не специфичный для дифференциальной эволюции: эффективность кроссовера в генетических алгоритмах

Answer 1

Я не особенно знаком со спецификой алгоритма DE, но в целом смысл кроссовера заключается в том, что если у вас есть два очень разных человека с высокой физической подготовкой, это даст потомство, которое является промежуточным между ними, не будучи особенно похожим ни на одного из них. Мутация только исследует местное соседство каждого человека без учета остальной части населения. Если вы думаете о геномах как о точках в некотором многомерном векторном пространстве, то мутация - это сдвиг в случайном направлении. Поэтому мутация должна предприниматься небольшими шагами, поскольку, если вы начинаете со значительно лучшего, чем случайного положения, длинный шаг в случайном направлении почти наверняка ухудшит положение, поскольку по сути это просто введение энтропии в эволюционирующий геном. Вы можете думать о переходе как шаг от одного родителя к другому. Поскольку другой родитель также лучше случайного, более перспективным будет сделать более длинный шаг в этом направлении. Это позволяет быстрее исследовать перспективные части фитнес-ландшафта.

В реальных биологических организмах геном часто организован таким образом, что гены, которые зависят друг от друга, находятся близко друг к другу на одной хромосоме. Это означает, что кроссовер вряд ли нарушит синергетические генные комбинации. Реальная эволюция фактически перемещает гены, чтобы достичь этого (хотя это намного медленнее, чем эволюция отдельных генов), и иногда структура генома более высокого порядка (трехмерная форма ДНК) развивается, чтобы предотвратить пересечения в особенно чувствительных областях, Эти механизмы редко смоделированы в эволюционных алгоритмах, но вы получите больше пользы от кроссоверов, если вы упорядочите свой геном таким образом, чтобы гены, вероятно, взаимодействовали друг с другом.

Answer 2

Как говорит Даниэль, кроссовер - это способ сделать более масштабные шаги в проблемной среде, позволяя вам избежать локальных максимумов, которые не могла бы сделать одна мутация.

Подходит ли это или нет, будет зависеть от сложности проблемного пространства, от того, как работает экспрессия генотипа -> фенотипа (будут ли связанные гены близки друг к другу) и т. Д.

Более формально это понятие "связности" в алгоритмах локального поиска, обеспечивающее достаточно сильных операторов, чтобы локальная окрестность поиска была достаточно большой, чтобы избежать локальных минимумов.

Answer 3

Нет. Кроссовер не полезен. Там я это сказал.:П

Я никогда не нашел потребность в кроссовере. Люди, кажется, думают, что это какая-то магия. Но он не делает (и не может) делать ничего более полезного, чем простая мутация. Большие мутации могут быть использованы для изучения всего проблемного пространства, а маленькие мутации могут использоваться для использования ниш.

И все объяснения, которые я прочитал, (мягко говоря) неудовлетворительные. Кроссовер только усложняет ваши алгоритмы. Брось как можно скорее. Ваша жизнь будет проще..... ПО МОЕМУ МНЕНИЮ.