Подгонка повторяющегося однофакторного эксперимента с gls, lme и gam

Question

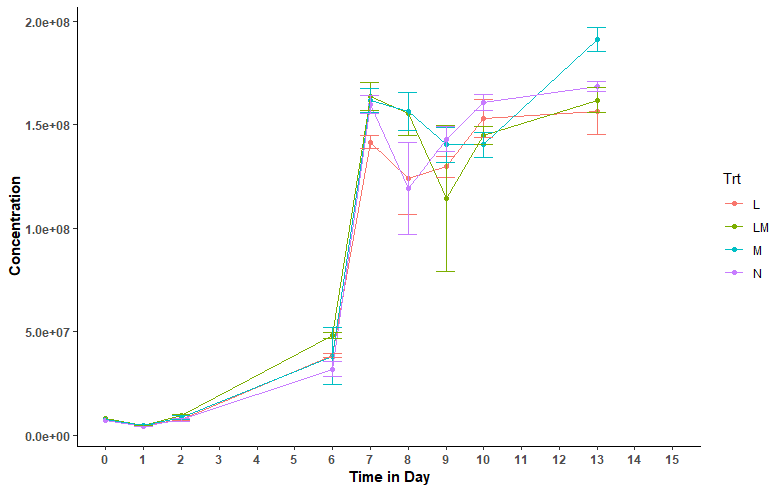
Базовый эксперимент: CRD с 4 обработками (N,L,M и ML) и 3 повторениями / трт. Итак, всего 12 прогонов / испытаний / предметов. Концентрацию каждого прогона определяли в день 0, 1,2,6,7, 9,10, 13 и 13, что в итоге составило 9 × 12 = 108 ак / точек данных.

Вот график данных.

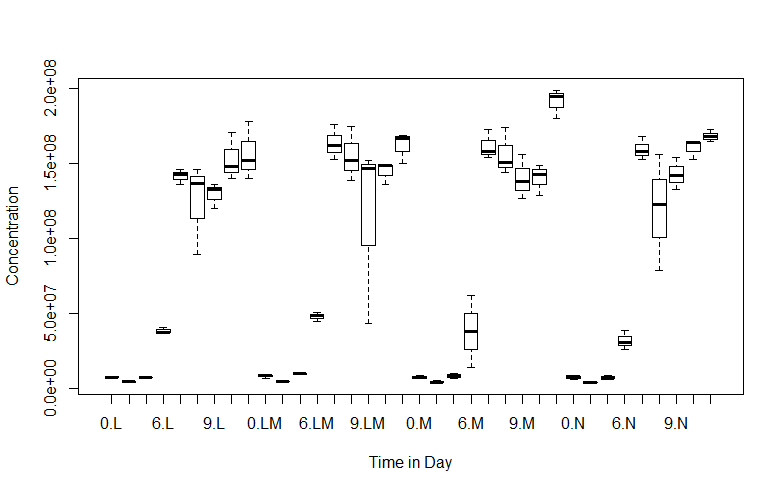
Boxplot всех комбинаций trt и day следующим образом.

Следующие модели были запущены.

1. ГЛС без корреляции

   conc.gls1<- gls (Conc ~ factor (Trt) * Day, data = data, method = "REML")

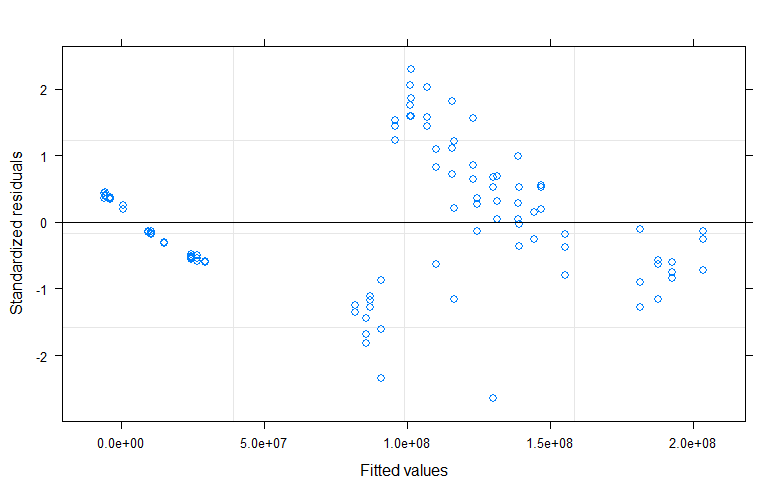
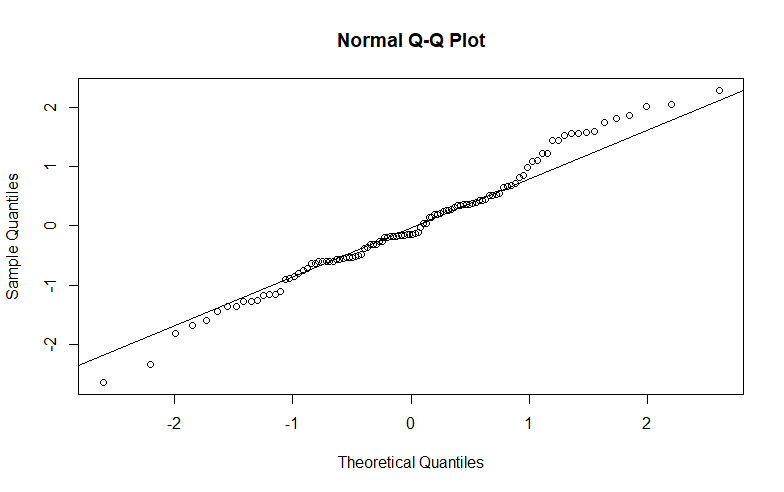
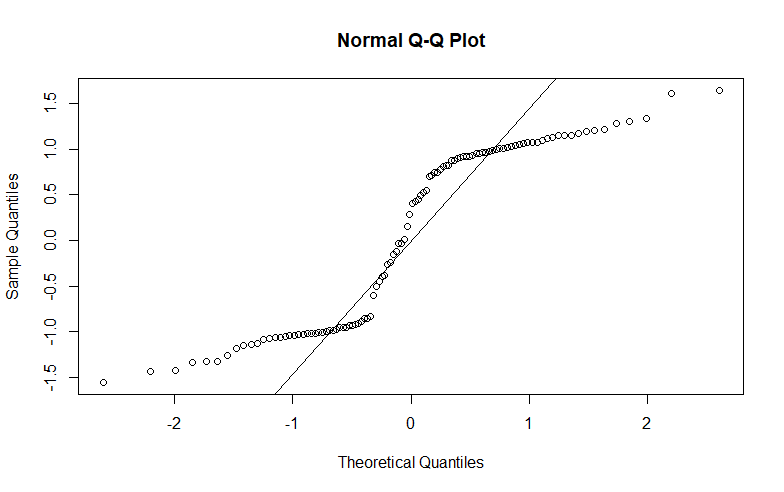
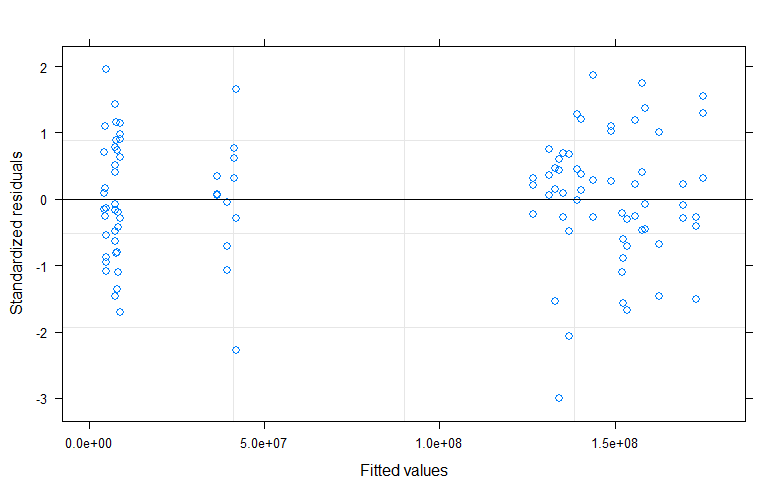
Остатки против Приспособленных и QQ Участков.

2. gls с ar(1) для каждого испытания / запуска в качестве субъекта

   conc.gls3<- gls (Conc ~ factor (Trt) * Day, data = data, weight = varIdent (form = ~ 1 | factor (Trt) * factor (Day)), корреляция = corAR1 (form = ~ Day | subject))

Остатки против Fitted и QQ сюжет.

3. Время со дня как случайный фактор

   conc.lme<- lme (Conc ~ factor (Trt) * Day, data = data, random = ~ 1 | Day, весовые коэффициенты = varIdent (form = ~ 1 | Day))

Остатки по сравнению с установленным и QQ участок

4. игра с днем ​​в качестве сглаживающей переменной

   conc.gam<- mgcv:: gam (Conc ~ factor (Trt) + s (Day, k = 6), data = data)

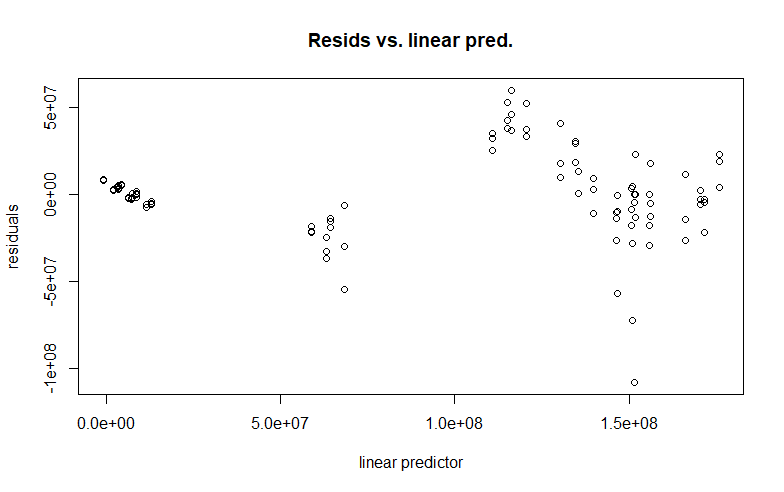
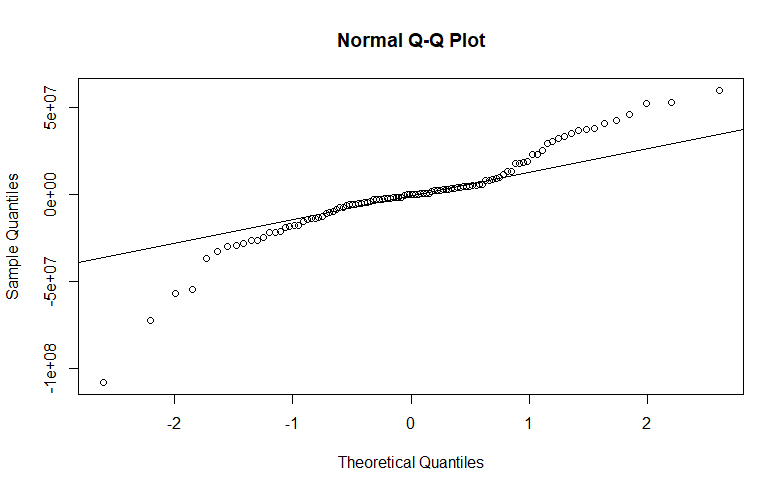
Остатки по сравнению с установленным и QQ участок

Вот АИК

                 df      AIC
conc.gls1  9.000000 3799.592
conc.gls2 45.000000 3731.522
conc.lme  18.000000 3533.088
conc.gam   9.936895 3998.234


All the models except the first one seem justified. 

The lme model seems to be the best: residuals vs fitted, qq plot, AIC all look great. But is it justified to treat day as a random factor? 

The gls2 seems to fit the experimental well, but the results were not satisfactory, probably due to the poor fit of the time series. Does anyone have a better way to model?

Ценю любые комментарии / предложения!