Построение числовой линии в Mathematica

Question

Я хотел бы нарисовать простой интервал на числовой линии в Mathematica. Как мне это сделать?

Answer 1

Вот еще одна попытка, которая рисует числовые линии с более обычными белыми и черными кружками, хотя любой графический элемент, который вы хотите, может быть легко заменен.

Опирается на LogicalExpand[Simplify@Reduce[expr, x]] а также Sort чтобы получить выражение в нечто похожее на каноническую форму, над которой могут работать правила замены. Это не всесторонне проверено и, вероятно, немного хрупко. Например, если данный expr сводится к True или же FalseМой код не умирает изящно.

numLine[expr_, x_Symbol:x, range:{_, _}:{Null, Null}, 
  Optional[hs:_?NumericQ, 1/30], opts:OptionsPattern[]] := 
 Module[{le = {LogicalExpand[Simplify@Reduce[expr, x]]} /. Or -> List,
   max, min, len, ints = {}, h, disk, hArrow, lt = Less|LessEqual, gt = Greater|GreaterEqual},
  If[TrueQ@MatchQ[range, {a_, b_} /; a < b],
   {min, max} = range,
   {min, max} = Through[{Min, Max}@Cases[le, _?NumericQ, \[Infinity]]]];
  len =Max[{max - min, 1}]; h = len hs;
  hArrow[{x1_, x2_}, head1_, head2_] := {{Thick, Line[{{x1, h}, {x2, h}}]},
                                         Tooltip[head1, x1], Tooltip[head2, x2]};
  disk[a_, ltgt_] := {EdgeForm[{Thick, Black}], 
    Switch[ltgt, Less | Greater, White, LessEqual | GreaterEqual, Black], 
    Disk[{a, h}, h]};
  With[{p = Position[le, And[_, _]]}, 
       ints = Extract[le, p] /. And -> (SortBy[And[##], First] &); 
       le = Delete[le, p]];   
  ints = ints /. (l1 : lt)[a_, x] && (l2 : lt)[x, b_] :> 
     hArrow[{a, b}, disk[a, l1], disk[b, l2]];
  le = le /. {(*_Unequal|True|False:>Null,*)
     (l : lt)[x, a_] :> (min = min - .3 len; 
       hArrow[{a, min}, disk[a, l], 
        Polygon[{{min, 0}, {min, 2 h}, {min - Sqrt[3] h, h}}]]),
     (g : gt)[x, a_] :> (max = max + .3 len; 
       hArrow[{a, max}, disk[a, g], 
        Polygon[{{max, 0}, {max, 2 h}, {max + Sqrt[3] h, h}}]])};
  Graphics[{ints, le}, opts, Axes -> {True, False}, 
   PlotRange -> {{min - .1 len, max + .1 len}, {-h, 3 h}},
   GridLines -> Dynamic[{{#, Gray}} & /@ MousePosition[
                           {"Graphics", Graphics}, None]], 
   Method -> {"GridLinesInFront" -> True}]
  ]

(Примечание: я изначально пытался использовать Arrow а также Arrowheads рисовать линии - но так как Arrowheads автоматически масштабирует стрелки в соответствии с шириной охватывающей графики, это доставляет мне слишком много головной боли.)

ОК, несколько примеров:

numLine[0 < x], 
numLine[0 > x]
numLine[0 < x <= 1, ImageSize -> Medium]

numLine[0 < x <= 1 || x > 2, Ticks -> {{0, 1, 2}}]

numLine[x <= 1 && x != 0, Ticks -> {{0, 1}}]

GraphicsColumn[{
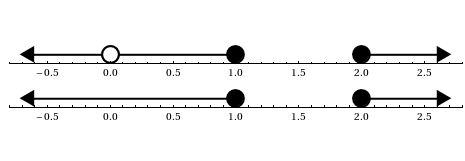
  numLine[0 < x <= 1 || x >= 2 || x < 0],
  numLine[0 < x <= 1 || x >= 2 || x <= 0, x, {0, 2}]
  }]

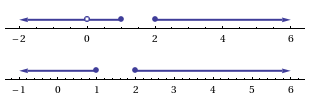
Редактировать: Давайте сравним вышеприведенное с выводом Wolfram|Alpha

WolframAlpha["0 < x <= 1 or x >= 2 or x < 0", {{"NumberLine", 1}, "Content"}]
WolframAlpha["0 < x <= 1 or x >= 2 or x <= 0", {{"NumberLine", 1}, "Content"}]

Обратите внимание (при просмотре вышеупомянутого в сеансе Mathematica или на веб-сайте W|A) причудливые всплывающие подсказки о важных точках и серых динамических линиях сетки. Я украл эти идеи и включил их в отредактированные numLine[] код выше.

Выход из WolframAlpha не совсем нормальный Graphics объект, поэтому трудно изменить его Options или объединить, используя Show, Чтобы увидеть различные объекты нумерации, которые Wolfram|Alpha может вернуть, запустите WolframAlpha["x>0", {{"NumberLine"}}] - "Content", "Cell" и "Input" возвращают в основном один и тот же объект. Во всяком случае, чтобы получить графический объект от

wa = WolframAlpha["x>0", {{"NumberLine", 1}, "Content"}]

Вы можете, например, запустить

Graphics@@First@Cases[wa, GraphicsBox[__], Infinity, 1]

Затем мы можем изменить графические объекты и объединить их в сетку, чтобы получить

Answer 2

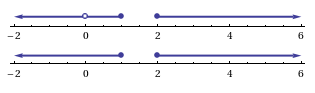
Для построения открытых или закрытых интервалов вы можете сделать что-то вроде:

intPlot[ss_, {s_, e_}, ee_] := Graphics[{Red, Thickness[.01],
   Text[Style[ss, Large, Red, Bold], {s, 0}],
   Text[Style[ee, Large, Red, Bold], {e, 0}],
   Line[{{s, 0}, {e, 0}}]},
  Axes -> {True, False},
  AxesStyle -> Directive[Thin, Blue, 12],
  PlotRange -> {{ s - .2 Abs@(s - e), e + .2 Abs@(s - e)}, {0, 0}},
  AspectRatio -> .1]

intPlot["[", {3, 4}, ")"]

редактировать

Ниже следует замечательное расширение, сделанное @Simon, которое я, вероятно, снова испортил, пытаясь решить проблему с перекрывающимися интервалами.

intPlot[ss_, {s_, e_}, ee_] := intPlot[{{ss, {s, e}, ee}}]
intPlot[ints : {{_String, {_?NumericQ, _?NumericQ}, _String} ..}] :=
 Module[{i = -1, c = ColorData[3, "ColorList"]},
  With[
   {min = Min[ints[[All, 2, 1]]], max = Max[ints[[All, 2, 2]]]},
   Graphics[Table[
     With[{ss = int[[1]], s = int[[2, 1]], e = int[[2, 2]], ee = int[[3]]}, 
       {c[[++i + 1]], Thickness[.01],
       Text[Style[ss, Large, c[[i + 1]], Bold], {s, i}], 
       Text[Style[ee, Large, c[[i + 1]], Bold], {e, i}],
       Line[{{s, i}, {e, i}}]}], {int, ints}], 
    Axes -> {True, False}, 
    AxesStyle -> Directive[Thin, Blue, 12], 
    PlotRange -> {{min - .2 Abs@(min - max), max + .2 Abs@(min - max)}, {0, ++i}}, 
    AspectRatio -> .2]]]

(*Examples*)

intPlot["[", {3, 4}, ")"]
intPlot[{{"(", {1, 2}, ")"}, {"[", {1.5, 4}, ")"}, 
        {"[", {2.5, 7}, ")"}, {"[", {1.5, 4}, ")"}}]

Answer 3

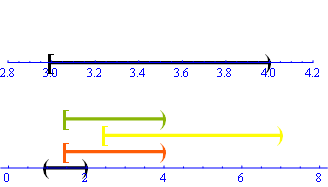
Вот уродливое решение, использующее RegionPlot, Открытые лимиты представлены пунктирными линиями, а закрытые лимиты - полными линиями.

numRegion[expr_, var_Symbol:x, range:{xmin_, xmax_}:{0, 0}, opts:OptionsPattern[]] :=
            Module[{le=LogicalExpand[Reduce[expr,var,Reals]],
                    y, opendots, closeddots, max, min, len},
 opendots =   Cases[Flatten[le/.And|Or->List], n_<var|n_>var|var<n_|var>n_:>n];
 closeddots = Cases[Flatten[le/.And|Or->List], n_<=var|n_>=var|var<=n_|var>=n_:>n];
 {max, min} = If[TrueQ[xmin < xmax], {xmin, xmax}, 
                 {Max, Min}@Cases[le, _?NumericQ, Infinity] // Through];
 len = max - min;
 RegionPlot[le && -1 < y < 1, {var, min-len/10, max+len/10}, {y, -1, 1},
            Epilog -> {Thick, Red, Line[{{#,1},{#,-1}}]&/@closeddots,
                       Dotted, Line[{{#,1},{#,-1}}]&/@opendots},
            Axes -> {True,False}, Frame->False, AspectRatio->.05, opts]]

Пример уменьшения абсолютного значения:

numRegion[Abs[x] < 2]

Можно использовать любую переменную:

numRegion[0 < y <= 1 || y >= 2, y]

Reduces посторонние неравенства, сравните следующее:

GraphicsColumn[{numRegion[0 < x <= 1 || x >= 2 || x < 0],
                numRegion[0 < x <= 1 || x >= 2 || x <= 0, x, {0, 2}]}]

Answer 4

Начиная с Mathematica 10, есть NumberLinePlot имеется в наличии.

Answer 5

Предыдущее уродливое решение помогло мне разработать функцию InequalityPlot для решения и построения графиков неравенств с двумя переменными.

InequalityPlot[ineq_, {x_Symbol, xmin_, xmax_},{y_Symbol, ymin_, ymax_},
  opts : OptionsPattern[Join[Options[ContourPlot],
    Options[RegionPlot], {CurvesColor -> RGBColor[1, .4, .2]}]]] :=
 Module[{le = LogicalExpand[ineq], opencurves, closedcurves, curves},
  opencurves = Cases[Flatten[{le /. And | Or -> List}],
   lexp_ < rexp_ | lexp_ > rexp_ | lexp_ < rexp_ | lexpr_ > rexp_ :>
    {lexp == rexp, Dashing[Medium]}];
  closedcurves = Cases[Flatten[{le /. And | Or -> List}],
   lexp_ <= rexp_ | lexp_ >= rexp_ | lexp_ <= rexp_ | lexp_ >= rexp_ :>
    {lexp == rexp, Dashing[None]}];
  curves = Join[opencurves, closedcurves];
  Show[  RegionPlot[ineq, {x, xmin, xmax}, {y, ymin, ymax},
    BoundaryStyle -> None,
    Evaluate[Sequence @@ FilterRules[{opts}, Options[RegionPlot]]]],
   ContourPlot[First[#] // Evaluate, {x, xmin, xmax}, {y, ymin, ymax},
      ContourStyle -> Directive[OptionValue[CurvesColor], Last[#]],
      Evaluate[Sequence @@ FilterRules[{opts},
         Options[ContourPlot]]]] & /@ curves  ]
 ]

Вот два примера:

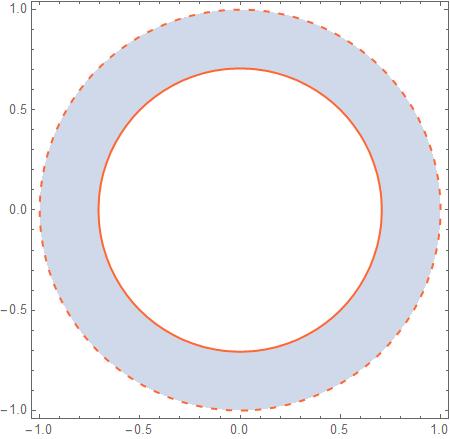
InequalityPlot[0.5 <= x^2 + y^2 < 1, {x, -1, 1}, {y, -1, 1}]

InequalityPlot[x^2 + y^2 < 0.5 && x + y <= 0.5,{x, -1, 1}, {y, -1, 1}]

Answer 6

Сделать регулярный Plotи установить Axes -> {True, False} (и скрыть ограничивающий прямоугольник, если он существует, чего обычно нет). Отрегулируйте размер изображения или соотношение сторон в зависимости от ситуации.

например

Plot[
    Piecewise[{
        {0, And[0<x, x<1]}
    }],
    {x,-1,2},
    Axes -> {True, False}        
]

Ты можешь использовать Show совместить это с представлением открытых и закрытых точек.

Существует небольшая вероятность, что вам, возможно, придется пройти в Indeterminate или какое-то другое специальное значение в качестве второго аргумента Piecewise (или по умолчанию он равен 0), если вы неправильно настроили ширину линии или похожие стили печати; или, альтернативно, но более надежно, установите значение 999 и PlotRange -> {{-1,2},{-.1,.1}},