Полностью отключить двудольный граф
У меня есть несвязный двунаправленный неориентированный граф. Я хочу полностью отключить график. Единственная операция, которую я могу выполнить - это удалить узел. Удаление узла автоматически удалит его ребра. Задача - минимизировать количество удаляемых узлов. Каждый узел в графе имеет не более 4 ребер.
Под полным отключением графа я подразумеваю, что никакие два узла не должны быть связаны через ссылку. В основном пустой набор ребер.
4 ответа
Я думаю, вы не можете доказать, что ваш алгоритм является оптимальным, потому что, на самом деле, он не является оптимальным.
Чтобы полностью отключить ваш граф, сводя к минимуму количество удаляемых узлов, вы должны удалить все узлы, принадлежащие минимальному покрытию вершин вашего графа. Поиск минимального покрытия вершин обычно является NP-полным, но для двудольных графов существует решение за полиномиальное время.
Найти максимальное соответствие в графе (возможно, с помощью алгоритма Хопкрофта – Карпа). Затем используйте теорему Кенига, чтобы получить минимальное покрытие вершин:
Рассмотрим двудольный граф, в котором вершины разбиты на левые (L) и правые (R) множества. Предположим, что существует максимальное совпадение, которое делит ребра на те, которые используются в сопоставлении (E_m), а те, которых нет (E_0). Пусть T состоит из всех несопоставленных вершин из L, а также всех вершин, достижимых из них, если идти слева направо по ребрам от E_0 и справа налево по ребрам от E_m. По сути, это означает, что для каждой несопоставленной вершины в L мы добавляем в T все вершины, которые встречаются на пути, чередующемся между ребрами из E_0 и E_m.
Тогда (L \ T) OR (R AND T) - минимальное покрытие вершин.
Вот контрпример к вашему предложенному алгоритму.
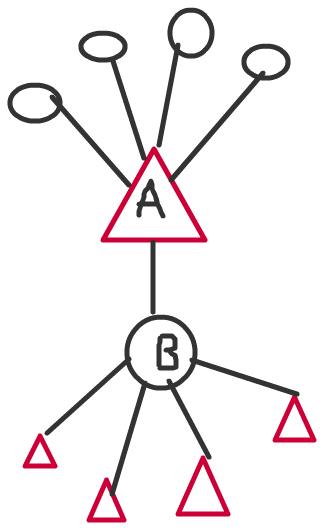
Лучшее решение - удалить оба узла A и B, даже если они разных цветов.
Поскольку все ребра от одного набора к другому, найдите эти два набора, используя, скажем, BFS, и раскрасьте, используя 2 цвета. Затем удалите узлы в меньшем наборе.
Поскольку между собой нет ребер, остальные узлы также отключены.
[В качестве шага предварительной обработки вы можете сначала пропустить узлы с 0 ребрами.]
Я придумал алгоритм для него, но не смог доказать, является ли он оптимальным.
Мой алгоритм: на каждом отключенном подграфе я запускаю BFS и соответствующим образом окрашиваю его. Затем я определяю количество узлов, окрашенных каждым цветом, и беру минимум двух и сохраняю. Я повторяю процедуру для каждого подграфа и суммирую, чтобы получить необходимый минимум. Помогите мне доказать алгоритм, если он правильный.
РЕДАКТИРОВАТЬ: приведенный выше алгоритм не является оптимальным. Принятый ответ проверен на правильность.