Странное поведение алгоритма муравьиных колоний
Я разработал алгоритм ACO. Я думаю, что это не работает должным образом... это будет трудно объяснить, но я постараюсь.
Проблема в том, что уровень феромонов плавающий. Я предполагаю, что уровень феромонов на лучшем пути должен увеличиваться все больше и больше, но в моей программе это не так.
Optimal path это путь, который строится путем нахождения максимального уровня феромона на ребрах между начальной и целевой вершинами.
Пример:
1 5 3
4 5 10
0 0 0
Optimal path будет 1 -> 2 -> 3,
Весовая матрица:
0 3 10
0 0 3
0 0 0
Лучший путь это: 1 -> 2 -> 3 (length: 6) Другой путь (не оптимальный): 1 -> 3 (length: 10)
Уровни феромонов после 10 муравьев:
0 5 1
0 0 3
0 0 0
Оптимальный путь: 1 -> 2 -> 3
Уровни феромонов после 20 муравьев (еще 10):
0 1 5
0 0 1
0 0 0
Оптимальный путь: 1 -> 3
Уровень феромонов после 30 муравьев:
0 4 1
0 0 3
0 0 0
Оптимальный путь: 1 -> 2 -> 3
Уровень феромонов после 30 муравьев:
0 4 6
0 0 2
0 0 0
Оптимальный путь: 1 -> 3
Это всего лишь пример, но он показывает, как выглядит матрица феромонов в моей программе.
Псевдокод моей программы:
init alpha, beta and other coef's
while antCount do
{
current = start
// + init visited array for current ant, some others variables
while vertexAvailable(current) do
{
find probabilities to go to 1
or another vertex
generate random number, choose next
vertex depending on it,
defining nextVertex
current = nextVertex
if current == stop then
{
get path length
update pheromones on path of current
ant depending on path length
}
}
evaporation of pheromones
antCount = antCount - 1
}
Итак, почему уровни феромонов в моей программе плавают? Почему лучший путь не имеет большинства уровней феромонов? Я понимаю, что в этом алгоритме есть фактор вероятности, но он все равно должен показывать правильный результат.
Что я делаю в своей программе? Здесь вы можете найти полный источник основного цикла моей программы.
1) Основной цикл - это цикл, который продолжается до тех пор, пока для текущей итерации не появятся муравьи.
1.1) В этом цикле у меня есть другой цикл (внутренний цикл), который будет запускаться до тех пор, пока у текущего муравья не будет вершин, к которым они могут идти (вершины не должны посещаться текущим муравьем).
Во внутреннем цикле я делаю это:
1.1.1) Расчет знаменателя уравнения ниже
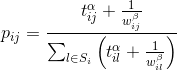
Эта формула рассчитает вероятность выбора ij дорожка (i текущий узел, j следующий узел).
Код:
var denom = 0;
for(col in graph[currentVertex])
{
// этот цикл формирует знаменатель формулы
var weight = graph[currentVertex][col];
if(weight != 0 && visited[col] != true)
{
var tau = pheromone[currentVertex][col];
denom = denom + getAttractiveness(tau, weight);
}
}
Кроме того, я добавил все вероятности в интервал, что поможет мне решить, какую вершину выбрать.
Код:
for(col in graph[currentVertex])
{
var weight = graph[currentVertex][col];
if(weight != 0 && visited[col] != true)
{
var tau = pheromone[currentVertex][col];
var nom = getAttractiveness(tau, weight);
var probability = nom/denom;
intervals[col] = probability+intervals.last;
intervals.last = probability+intervals.last;
}
}
1.1.3) Создание случайного числа от 0 до 1 и выбор вершины на основе intervals массив, определенный в предыдущей части кода
Код:
var rand = Math.random();
var nextVertex = 0;
for(vertex in intervals)
{
if (rand < intervals[vertex])
{
nextVertex = parseInt(vertex,10);
break;
}
}
1.1.4) Некоторые инструкции, настройка помощников (путь помощника, посещение, помощь) и т. Д.
1.1.5) Следующим шагом я проверяю, является ли найденная вершина вершина цели
Если да (это значит, что муравей нашел вершину цели), я делаю это:
1.1.5.1) Получение длины текущего пути муравья
Код:
var length = 0;
while(source = pathCopy.pop())
{
console.log("dest: " + dest + " source: " + source);
length = length + graph[source][dest];
dest = source;
}
1.1.5.2) Обновление уровня феромонов на этом пути
Код:
var deltaTau = 5/length;
var dest = path.pop();
var source;
while(source = path.pop())
{
var oldPheromone = pheromone[source][dest];
// обновление феромона формула 3
var newPheromone = oldPheromone+deltaTau;
// console.log('pheromone levels: old =
// '+oldPheromone+' new = ' + newPheromone);
pheromone[source][dest] = newPheromone;
dest = source;
}
1.2) В конце основного цикла я делаю испарение уровней феромона:
Код:
for(row in pheromone)
{
for(col in pheromone[row])
{
var oldPheromone = pheromone[row][col];
// обновление феромона формула 3
var newPheromone = (1-ktau)*oldPheromone;
pheromone[row][col] = newPheromone;
}
}
1 ответ
При выборе следующего пути ваш код всегда выбирает первую соседнюю вершину ниже случайного порога. Я не уверен, как это должно представлять муравьев, идущих к вершинам с большим количеством феромонов. Этот метод будет работать в той степени, в которой концентрация феромонов относительно низкая (ниже 0,5). Тем не менее, в областях, где концентрация феромонов высока (около или выше 1), потому что ваш random() число от 0 до 1, вы вернетесь к выбору первой доступной вершины. Вероятно, поэтому вы не сходитесь.