Алгоритм VF2 шаги с примером

Может кто-нибудь объяснить шаги алгоритма VF2 для изоморфизма графов простыми словами? Я изучаю этот алгоритм, но он груб без рабочего примера. Может ли кто-нибудь привести меня в правильном направлении? Спасибо.

Источник

2 ответа

Решение

Я постараюсь дать вам быстрое объяснение моего предыдущего ответа на этот вопрос:

Любой рабочий пример алгоритма VF2?

Я буду использовать тот же пример, что и в моем предыдущем ответе:

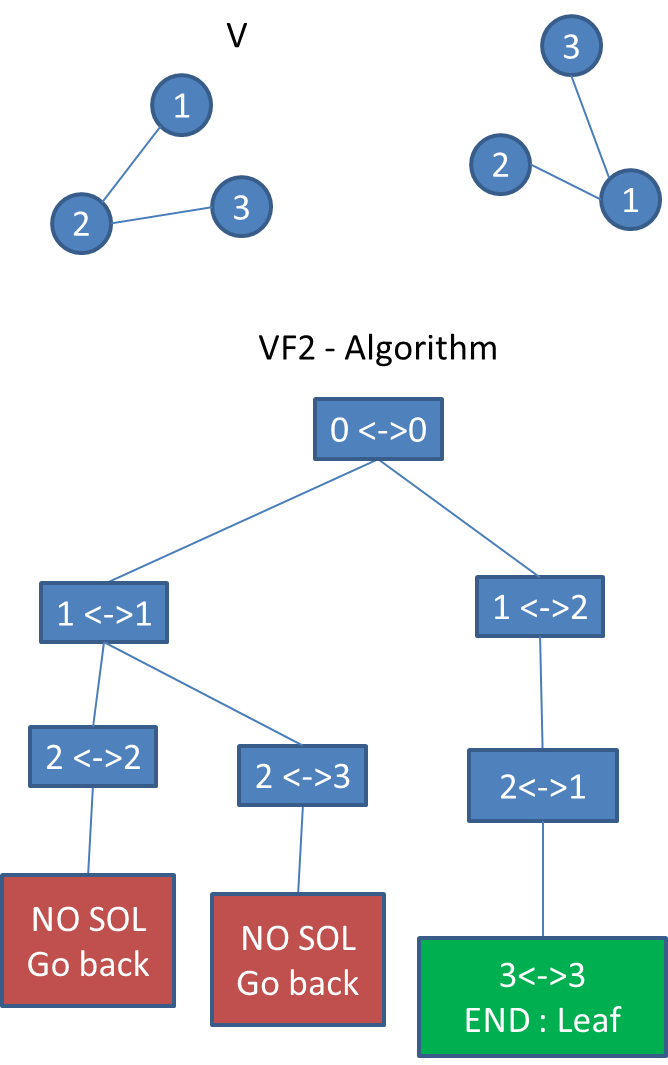
2 приведенных выше графика - это V и V' .(V' не на рисунке, но тот, что справа)

Алгоритм VF2 описан на графике.

Шаг за шагом

Я хочу знать, изоморфны ли V и V '.

Я буду использовать следующие обозначения: XV это узел X в V

В алгоритме VF2 я попытаюсь сопоставить каждый узел в V с узлом в V '.

шаг 1:

Я сопоставляю пустой V с пустым V ': это всегда работает

шаг 2: я могу сопоставить 1 В с 1 В ', 2 В' или 3 В '

Я сопоставляю 1V с 1V ': это всегда работает

шаг 3:

Я могу сопоставить 2V с 2V 'или 3V'

Я сопоставляю 2V с 2V ': это работает, потому что {1V 2V} и {1V' 2V} изоморфны

шаг 4:

Я пытаюсь сопоставить 3V с узлом в V ': я не могу! {было бы возможно, если бы был ребро между узлами 3 и 2 в V ', и не было ребра между 3 и 1)

Итак, я возвращаюсь к шагу 2

шаг 5:

Я сопоставляю 2V с 3V '

шаг 6:

так же, как шаг 4

Я возвращаюсь к шагу 2. На шаге 2 нет решения, я возвращаюсь к шагу 1

шаг 7:

Я соответствую 1V с 2V '

шаг 8:

Я сопоставляю 2V с 1V '

шаг 9:

Я сопоставляю 3V с 3V '

это работает, я соответствовал {1V 2V 3V} с { 2V' 1V' 3V'}

Графы изоморфны.

Если я протестирую все решение и оно никогда не сработает, график не будет изоморфным.

Надеюсь это поможет

По поводу вашего вопроса о "сопоставлении", посмотрите статью в Википедии об изоморфизме графа:

http://en.wikipedia.org/wiki/Graph_isomorphism

это хороший пример функции f, которая соответствует графу G и H: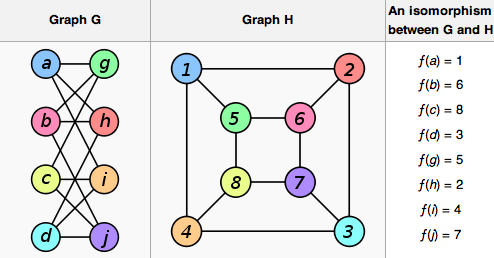

Надеюсь, вы сможете лучше понять этот алгоритм на этой иллюстрации.

Источник

Обзор высокого уровня алгоритма VF представлен:

ПРОЦЕДУРА Матч (ы)
    ВХОД: промежуточное состояние s; начальное состояние s0 имеет M(s0)=
    ВЫХОД: отображение между двумя графиками
    IF M (s) покрывает все узлы G2 THEN
        ВЫХОД М (с)
    ELSE
        Вычислить множество P (s) пар кандидатов на включение в M(s)
        FOREACH (n, m) P(s)
            ЕСЛИ F(s, n, m) ТО
                Вычислить состояние s´, полученное путем добавления (n, m) к M(s)
                CALL Match(s)
            КОНЕЦ ЕСЛИ
        КОНЕЦ ИССЛЕДОВАНИЯ
         Восстановить структуры данных
    КОНЕЦ ЕСЛИ
КОНЕЦ ПРОЦЕДУРЫ
Источник
Другие вопросы по тегам