Амортизированный анализ алгоритмов

Question

Я сейчас читаю амортизированный анализ. Я не в состоянии полностью понять, чем он отличается от обычного анализа, который мы выполняем для вычисления среднего или наихудшего поведения алгоритмов. Может кто-нибудь объяснить это на примере сортировки или что-то?

Answer 1

Амортизированный анализ дает среднюю производительность (по времени) каждой операции в худшем случае.

В последовательности операций наихудший случай не возникает часто в каждой операции - некоторые операции могут быть дешевыми, некоторые могут быть дорогими. Поэтому традиционный анализ наихудшего случая на операцию может дать чрезмерно пессимистическую оценку. Например, в динамическом массиве только некоторые вставки занимают линейное время, а другие - постоянное время.

Когда разные вставки занимают разное время, как мы можем точно рассчитать общее время? Амортизированный подход предусматривает присвоение "искусственной стоимости" каждой операции в последовательности, называемой амортизированной стоимостью операции. Требуется, чтобы общая реальная стоимость последовательности была ограничена суммой амортизированных затрат всех операций.

Обратите внимание, что иногда существует гибкость в распределении амортизированных затрат. Три метода используются в амортизированном анализе

1. Совокупный метод (или грубая сила)
2. Метод учета (или метод банкира)
3. Потенциальный метод (или метод физика)

Например, предположим, что мы сортируем массив, в котором все ключи различны (так как это самый медленный случай, и занимает столько же времени, сколько и нет, если мы не делаем ничего особенного с ключами, равными поворот).

Быстрая сортировка выбирает случайный опорный пункт. Скорее всего, стержень будет самым маленьким ключом, вторым самым маленьким, третьим самым маленьким, ... или самым большим. Для каждого ключа вероятность составляет 1/n. Пусть T(n) - случайная величина, равная времени выполнения быстрой сортировки по n различным ключам. Предположим, что быстрая сортировка выбирает i-й наименьший ключ в качестве оси. Затем мы запускаем быструю сортировку рекурсивно для списка длины i - 1 и для списка длины n - i. Требуется O(n) время, чтобы разделить и объединить списки - скажем, самое большее n долларов - поэтому время выполнения

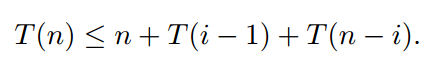
Здесь i - случайная переменная, которая может быть любым числом от 1 (pivot - наименьший ключ) до n (pivot - наибольший ключ), каждая из которых выбрана с вероятностью 1/n, поэтому

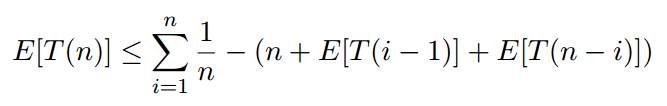
Это уравнение называется повторением. Базовые случаи для повторения: T(0) = 1 и T(1) = 1. Это означает, что сортировка списка нулевой длины или одного занимает максимум один доллар (единицу времени).

Итак, когда вы решаете:

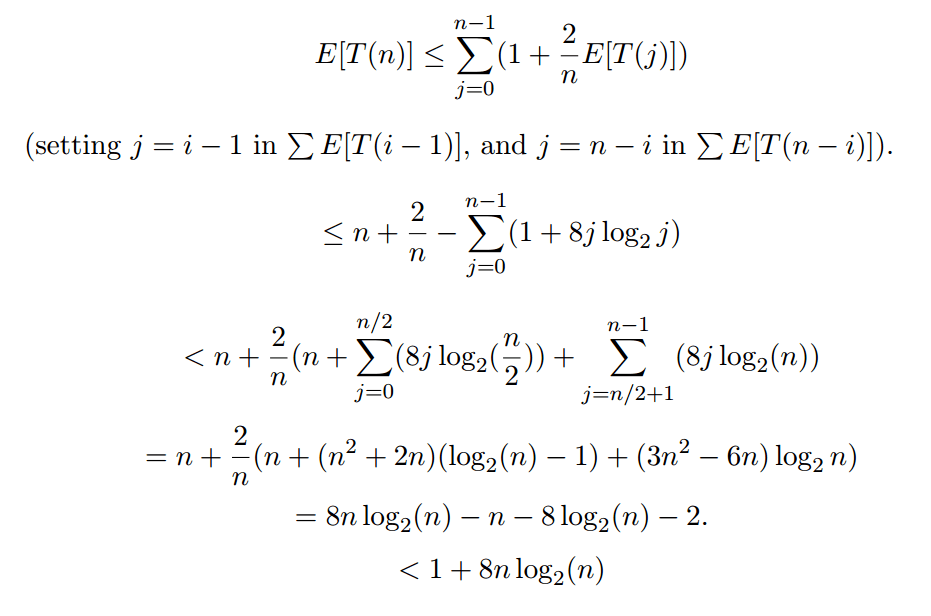
Выражение 1 + 8j log_2 j может быть завышенным, но это не имеет значения. Важным моментом является то, что это доказывает, что E[T(n)] находится в O(n log n). Другими словами, ожидаемое время выполнения быстрой сортировки находится в O(n log n).

Также есть тонкое, но важное различие между амортизированным временем работы и ожидаемым временем работы. Быстрая сортировка со случайными поворотами занимает O (n log n) ожидаемое время выполнения, но его наихудшее время выполнения находится в Θ(n^2). Это означает, что существует небольшая вероятность того, что быстрая сортировка будет стоить (n ^ 2) долларов, но вероятность того, что это произойдет, приближается к нулю при увеличении n.

Быстрая сортировка O (n log n) ожидаемое время
Быстрый выбор Θ(n) ожидаемое время

Для числового примера:

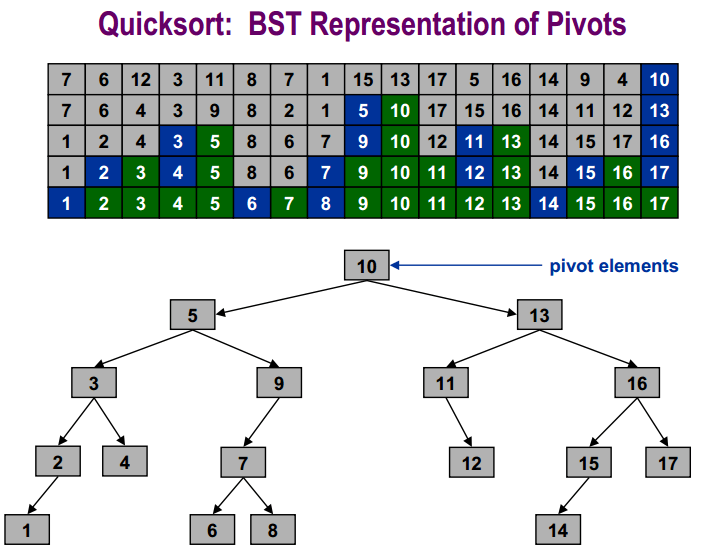
Сравнительная нижняя граница сортировки:

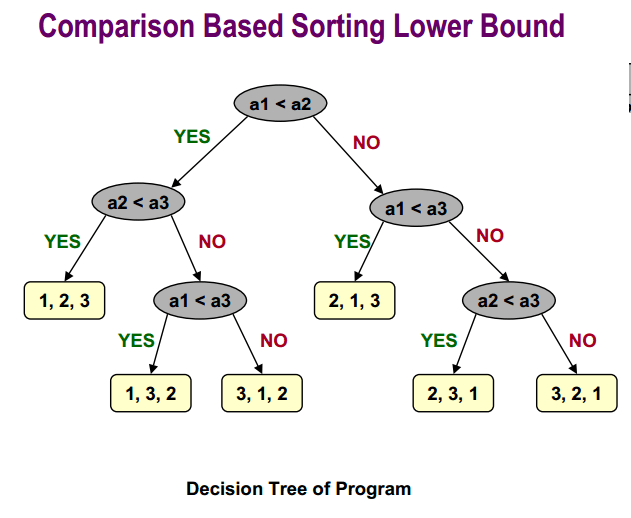
Наконец, вы можете найти более подробную информацию об анализе среднего случая быстрой сортировки здесь

Answer 2

среднее значение - вероятностный анализ, среднее значение по отношению ко всем возможным входам, это оценка вероятного времени выполнения алгоритма.

Амортизированный - не вероятностный анализ, рассчитанный по отношению к серии обращений к алгоритму.

пример - стек динамического размера:

скажем, мы определяем стек некоторого размера, и всякий раз, когда мы используем пространство, мы выделяем вдвое больший размер и копируем элементы в новое место.

В целом наши расходы:

• O (1) за вставку \ удаление

• O(n) на вставку (выделение и копирование), когда стек заполнен

так что теперь мы спрашиваем, сколько времени займет n вставок?

Можно сказать, O(n^2), однако мы не платим O(n) за каждую вставку. так что мы пессимистичны, правильный ответ - O(n) время для n вставок, давайте посмотрим, почему:

допустим, мы начинаем с размера массива = 1.

игнорируя копирование, мы будем платить O(n) за n вставок.

Теперь мы делаем полную копию только тогда, когда в стеке есть такое количество элементов:

1,2,4,8,..., п /2, п

для каждого из этих размеров мы делаем копию и выделяем, так что для суммирования мы получаем:

const * (1 + 2 + 4 + 8 +... + n / 4 + n / 2 + n) = const * (n + n / 2 + n / 4 +... + 8 + 4 + 2 + 1) <= const * n (1 + 1/2 + 1/4 + 1/8 +...)

где (1+1/2+1/4+1/8+...) = 2

поэтому мы платим O(n) за все копирование + O(n) за фактические n вставок

O(n) наихудший случай для операции n -> O(1) амортизируется за одну операцию.