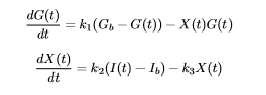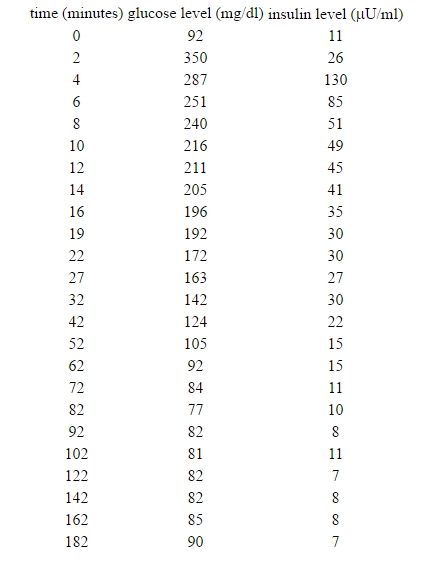Система дифференциальных уравнений с ode45 в matlab

Question

У меня есть эта модель для глюкозы и инсулина, а также система дифференциальных уравнений:

Куда:

G(t) - концентрация глюкозы в плазме в момент времени t
I(t) - концентрация инсулина в плазме в момент времени t
X(t)- интерстициальный инсулин в момент времени t
Gb - базальная концентрация глюкозы в плазме
Ib - базальная концентрация инсулина в плазме

которые описывают модель. Я должен сделать алгоритм для оценки параметров с использованием ode45 в Matlab.

Тестовые данные следующие:

Я не уверен, как написать функцию для ode45, моя идея заключается в следующем:

function [] = cwiczenie3_1a(dane)
a=size(dane);
u=[];
y=[];
for i=1:a(1,1)
  g(i,1)=dane(i,2);
  j(i,1)=dane(i,3);
end
[x t]=ode45(@funkcjajeden,[0 100],[0,0]) 
end

function [dg] = funkcjajeden(t,g)
gb=350;
d=0.1;
ib=120;
k1=1;
k2=2;
k3=1;
dg=zeros(size(g));
dg(1)=(k1*(gb-g(1)))-d*g(1);
dg(2)=(k2*(g(2)-ib))-k3*d;
end

Answer 1

Взглянув на документацию для ode45, чтобы решить систему дифференциальных уравнений, вы должны записать функцию в файл, odefcn.m в этом случае:

function dg = odefcn(g,k1,k2,k3,gb,ib,d)

  dg = zeros(size(g));
  dg(1) = k1*(gb-g(1)) - d*g(1);
  dg(2) = k2*(g(2)-ib) - k3*d;

И затем в другом файле вы решаете это, выполнив:

gb = 350;
d = 0.1;
ib = 120;
k1 = 1;
k2 = 2;
k3 = 1;

tspan = [0 100];
g0 = [0 0];
[t,g] = ode45(@(t,g) odefcn(g,k1,k2,k3,gb,ib,d), tspan, g0);

plot(t,g(:,1),t,g(:,2))

Таким образом, вы получите значения для обоих G(t) I(t) для этого начальные значения и параметры:

Образ

Затем вы можете сравнить с данными испытаний и найти значение параметров.