Определить, пересекаются ли два отрезка, используя Cramer
Я использовал код, который был размещен здесь. Вот код снова:
from __future__ import division
def line(p1, p2):
A = (p1[1] - p2[1])
B = (p2[0] - p1[0])
C = (p1[0]*p2[1] - p2[0]*p1[1])
return A, B, -C
def intersection(L1, L2):
D = L1[0] * L2[1] - L1[1] * L2[0]
Dx = L1[2] * L2[1] - L1[1] * L2[2]
Dy = L1[0] * L2[2] - L1[2] * L2[0]
if D != 0:
x = Dx / D
y = Dy / D
return x,y
else:
return False
# Usage
L1 = line([0,1], [2,3])
L2 = line([2,3], [0,4])
R = intersection(L1, L2)
if R:
print "Intersection detected:", R
else:
print "No single intersection point detected"
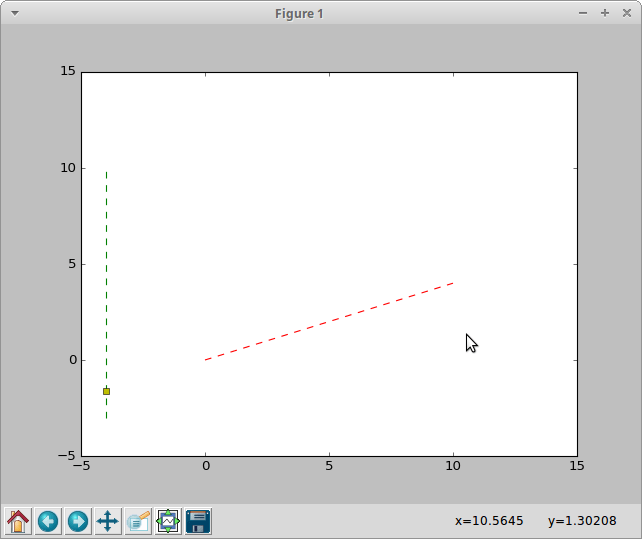
Он реализует правило Крамера (адаптировано для линий; если определитель линейного уравнения, построенного для двух заданных линий, равен 0, то линии не пересекаются). Однако проблема, с которой я столкнулся, заключается в том, что он также обнаруживает пересечения, которые являются результатом продолжения двух линий под рукой. Вот сюжет, который я сделал, используя matplotlib который демонстрирует проблему:
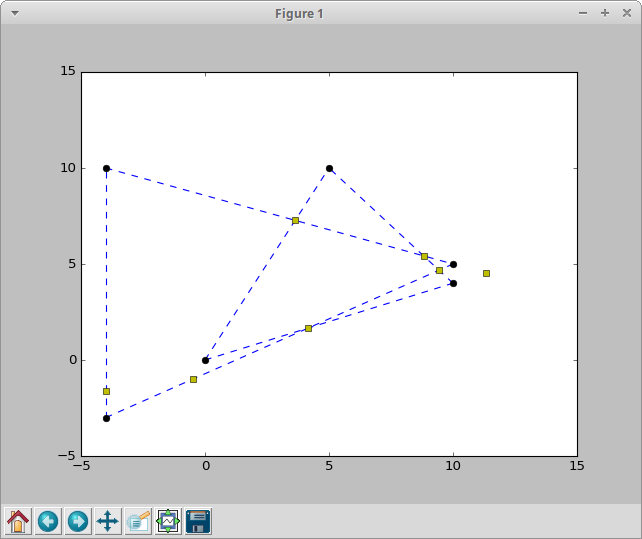
у меня тоже есть Triangle класс, который содержит 3 Line объекты, и это демонстрирует проблему еще дальше, так как класс также имеет свой собственный intersect(...) функция, которая берет другой треугольник и проверяет, какие ребра обоих треугольников пересекаются и где:
Я хочу обнаружить пересечение отрезка, используя алгоритм по ссылке. Вышеуказанные отрезки не имеют пересечения. Как я могу это сделать?
У меня есть два класса - Point а также Line - которые используются для работы с этими геометрическими элементами более читабельным способом. Я сохранил приведенный выше сценарий и обернул его вокруг (см. Line.intersect(...)):
class Point:
def __init__(self, x, y, z):
self.x = x
self.y = y
self.z = z
# Override __add__, __sub__ etc. to allow arithmetic operations with Point objects
# ...
class Line:
def __init__(self, p1, p2):
self.p1 = p1
self.p2 = p2
# ...
def intersect(self, l):
def line(p1, p2):
A = (p1.y - p2.y)
B = (p2.x - p1.x)
C = (p1.x*p2.y - p2.x*p1.y)
return A, B, -C
L1 = line(self.p1, self.p2)
L2 = line(l.p1, l.p2)
D = L1[0]*L2[1] - L1[1]*L2[0]
Dx = L1[2]*L2[1] - L1[1]*L2[2]
Dy = L1[0]*L2[2] - L1[2]*L2[0]
if D != 0:
x = Dx / D
y = Dy / D
p = Point(x, y)
return True, p
return False, None
#Usage
l1 = Line(Point(0, 0), Point(10, 4))
l2 = Line(Point(-4, -3), Point(-4, 10))
res, p = l1.intersect(l2)
if not res:
print('Lines don\'t intersect')
else:
print('Lines intersect at [%f, %f]' % (p.x, p.y))
Я также ищу оптимальное (как можно меньше дорогостоящих операций с минимальным объемом памяти).
Одно из возможных решений - отфильтровать полученные точки пересечения (те, которые не являются частью обоих сегментов), используя евклидово расстояние, чтобы определить, лежат ли эти точки на обоих сегментах или нет. Если нет, то пересечение является результатом продолжения одной или обеих линий и должно считаться недействительным. Это, однако, дорогостоящая операция, которая также включает в себя учет всех точек пересечения (независимо от того, является ли точка частью обоих сегментов или нет).
ОБНОВЛЕНИЕ: я думал, что решил проблему, но увы! у следующего есть проблема. Внимательно изучив комментарии, я увидел комментарий, сделанный @JerryCoffin, который указал на возможный дубликат этого поста:
def intersect(self, l, contious=False):
# Before anything else check if lines have a mutual abcisses
interval_1 = [min(self.p1.x, self.p2.x), max(self.p1.x, self.p2.x)]
interval_2 = [min(l.p1.x, l.p2.x), max(l.p1.x, l.p2.x)]
interval = [
min(interval_1[1], interval_2[1]),
max(interval_1[0], interval_2[0])
]
if interval_1[1] < interval_2[0]:
print('No mutual abcisses!')
return False, None
# Try to compute interception
def line(p1, p2):
A = (p1.y - p2.y)
B = (p2.x - p1.x)
C = (p1.x*p2.y - p2.x*p1.y)
return A, B, -C
L1 = line(self.p1, self.p2)
L2 = line(l.p1, l.p2)
D = L1[0]*L2[1] - L1[1]*L2[0]
Dx = L1[2]*L2[1] - L1[1]*L2[2]
Dy = L1[0]*L2[2] - L1[2]*L2[0]
if D != 0:
x = Dx / D
y = Dy / D
p = Point(x, y)
if contiuous: # continuous parameter allows switching between line and line segment interception
return True, p
else:
if p.x < interval[1] or p.x > interval[0]:
print('Intersection out of bound')
return False, None
else:
return True, p
else:
print('Not intersecting')
return False, None
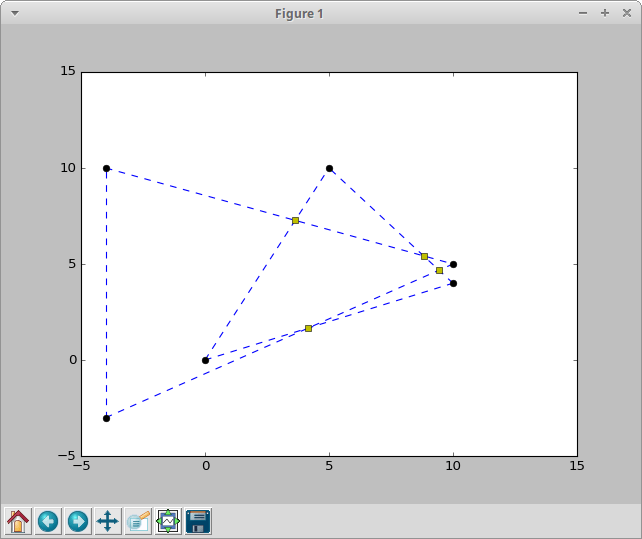
Результат:
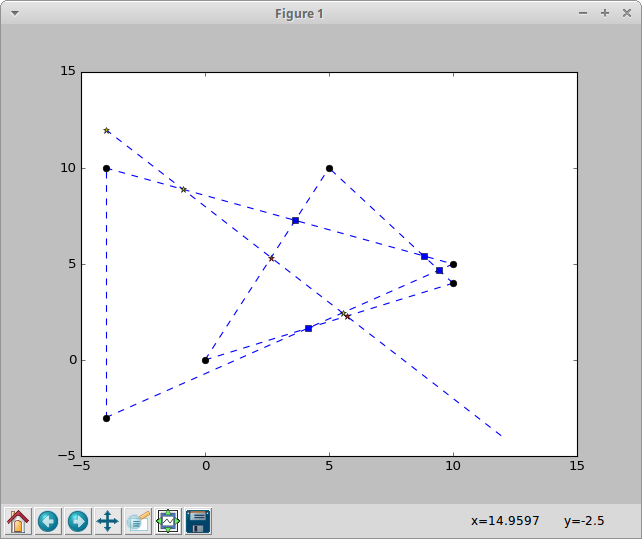
который выглядит красиво и именно то, что я хочу иметь. Однако я добавил строку (координаты были более или менее случайными, но мне было легко проверить на графике), а именно Line(Point(-4, 12), Point(12, -4)), И представьте мое удивление, когда я снова получил один ложный положительный результат:
Как вы можете видеть, в верхнем левом углу в начале моего отрезка обнаружена точка пересечения. Он действительно пересекается с продолжением вертикальной линии, но не с действительным отрезком. Кажется, тот факт, что оба отрезка имеют одинаковые x в то время как тот, который является вертикальным, создает проблему. Поэтому я до сих пор не знаю, как решить проблему.
1 ответ
Что ж, нужно научиться читать... Решение было на самом деле в комментариях в дублирующем предложении, сделанном @JerryCoffin, а именно здесь:
def intersect(self, l, contious=False):
# Before anything else check if lines have a mutual abcisses
interval_1 = [min(self.p1.x, self.p2.x), max(self.p1.x, self.p2.x)]
interval_2 = [min(l.p1.x, l.p2.x), max(l.p1.x, l.p2.x)]
interval = [
min(interval_1[1], interval_2[1]),
max(interval_1[0], interval_2[0])
]
if interval_1[1] < interval_2[0]:
print('No mutual abcisses!')
return False, None
# Try to compute interception
def line(p1, p2):
A = (p1.y - p2.y)
B = (p2.x - p1.x)
C = (p1.x*p2.y - p2.x*p1.y)
return A, B, -C
L1 = line(self.p1, self.p2)
L2 = line(l.p1, l.p2)
D = L1[0]*L2[1] - L1[1]*L2[0]
Dx = L1[2]*L2[1] - L1[1]*L2[2]
Dy = L1[0]*L2[2] - L1[2]*L2[0]
if D != 0:
x = Dx / D
y = Dy / D
p = Point(x, y)
if contiuous: # continuous parameter allows switching between line and line segment interception
return True, p
else:
if p.x < interval[1] or p.x > interval[0]:
print('Intersection out of bound')
return False, None
else:
return True, p
else:
print('Not intersecting')
return False, None
Результат: