Mathematica NDSolve

У меня есть вопрос о функции NDSolve в Mathematica. У меня есть генератор, определяемый этими двумя уравнениями:

x' = v
v' = -x - u*v^3

где и есть некоторая константа.

Как создать NDSolve, который решает эту проблему? Я пробовал следующий код (он должен зависеть от времени), но он не работает:

eq1 = x'[t] == v;
eq2 = v' == -x[t] - u*v^3;
eq3 = x[0] == 2;

(начальное смещение 2м).

s = NDSolve[{eq1, eq2, eq3}, x, {t, 0, 30}]

Большое спасибо...

Источник

2 ответа

Решение

Необходимо заметить, что первое уравнение когда-то дифференцировалось по отношению к t может быть использован для замены v[t], Но затем второе уравнение становится ОДУ второго порядка и требует предоставления другого дополнительного начального условия. Мы дадим

v[0]==x'[0]==some number

Затем после решения этого ODE для x вы можете восстановить v[t]==x'[t]Я даю вам решение в терминах Manipulate так что геометрически ситуация становится понятной для вас.

(* First equation *)
v[t] = x'[t];
(* 
   Differentiate this equation once and substitute 
   for v[t] in the second equation
*)
Manipulate[
With[{u = Constant, der = derval}, 
     res = NDSolve[{x''[t] == -x[t] - u*x'[t]^3, x[0.] == 2,x'[0.] == der},
     x, {t, 0., 30.}] // First; 
     Plot[Evaluate[{x[t], v[t]} /. res], {t, 0, 30}, PlotRange -> All,
     Frame -> True,Axes -> None, ImageSize -> 600]
   ],
{{Constant, 0.,TraditionalForm@(u)}, 0.,3, .1},
{{derval, -3., TraditionalForm@(v[0] == x'[0])}, -3, 3, .1}
]

Надеюсь, это поможет вам, но в следующий раз, прежде чем вы спросите, вам нужно сначала освежить теорию, так как вы видите вопрос, который вы задали, касающийся очень элементарной и элементарной математики, а не программирования Mathematica. Удачи!!

Источник

Вам нужно указать числовое значение для вашего u а также начальное условие для v[t]:

u=1.0;
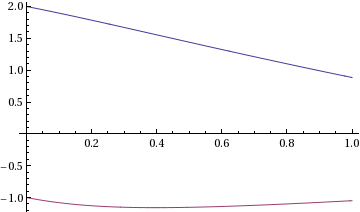
solution=NDSolve[{x'[t]==v[t], v'[t]==-x[t]-u v[t]^3,x[0]==2,v[0]==-1},{x,v},{t,0,1}]

Plot[{solution[[1,1,2]][t],solution[[1,2,2]][t]},{t,0,1}]

Источник
Другие вопросы по тегам