Построение серии 2D-проекций в 3D перспективным способом

Question

Я хотел бы построить распределение правдоподобия, в основном, матрицу NxT, где каждая строка представляет распределение по некоторой переменной на каждом временном шаге t (t = 0... T), чтобы я мог визуализировать траекторию, которую могла бы дать оценка максимального правдоподобия Уступать.

Я представляю несколько 2D-графиков, один перед другим - что-то вроде этого:

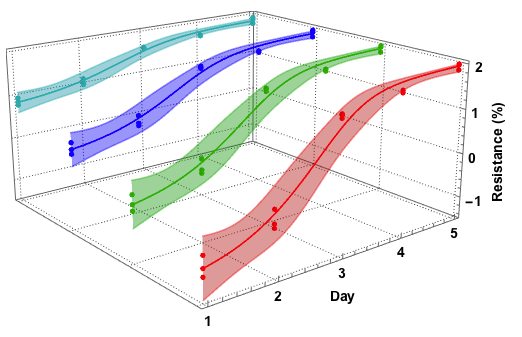
пока на основании этого я пробовал:

def TrajectoryPlot(P):
    P=P[0:4]  
    fig = plt.figure()
    ax = fig.gca(projection='3d')
    def cc(arg):
        return colorConverter.to_rgba(arg, alpha=0.6)
    xs = np.arange(0, len(P[0]))
    verts = []
    zs = [0.0, 1.0, 2.0, 3.0, 4.0]
    for i in range(len(P)):
        print(i)
        verts.append(list(zip(xs,  P[i])))    
    poly = PolyCollection(verts, facecolors=[cc('r'), cc('g'), cc('b'),
                                             cc('y')])
    poly.set_alpha(0.7)
    ax.add_collection3d(poly, zs=zs, zdir='y')
    ax.set_xlabel('X')
    ax.set_ylabel('Likelihood')
    ax.set_zlabel('Time')
    plt.show()

Но это еще не работает.

Answer 1

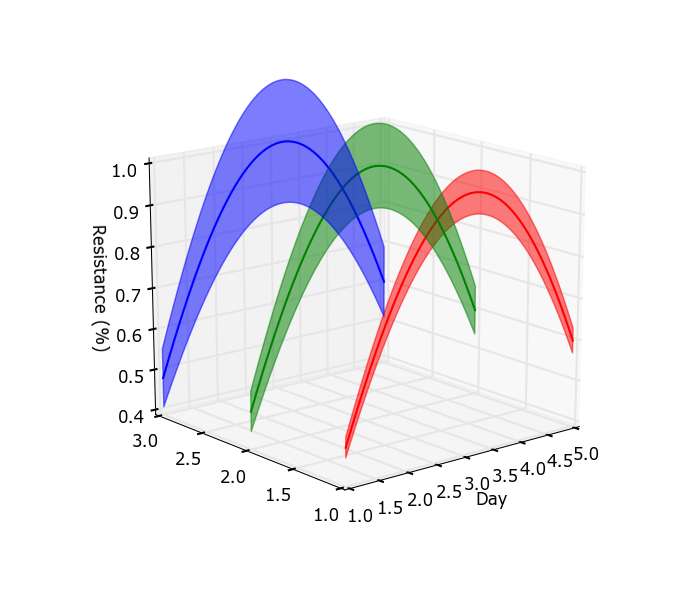
fill_between рутина также возвращает PolyCollection объект, чтобы вы могли использовать fill_between и добавить, что с помощью add_collection3d:

import matplotlib.pylab as pl
from mpl_toolkits.mplot3d import Axes3D
import numpy as np

x   = np.linspace(1,5,100)
y1  = np.ones(x.size)
y2  = np.ones(x.size)*2
y3  = np.ones(x.size)*3
z   = np.sin(x/2)

pl.figure()
ax = pl.subplot(projection='3d')
ax.plot(x, y1, z, color='r')
ax.plot(x, y2, z, color='g')
ax.plot(x, y3, z, color='b')

ax.add_collection3d(pl.fill_between(x, 0.95*z, 1.05*z, color='r', alpha=0.3), zs=1, zdir='y')
ax.add_collection3d(pl.fill_between(x, 0.90*z, 1.10*z, color='g', alpha=0.3), zs=2, zdir='y')
ax.add_collection3d(pl.fill_between(x, 0.85*z, 1.15*z, color='b', alpha=0.3), zs=3, zdir='y')

ax.set_xlabel('Day')
ax.set_zlabel('Resistance (%)')