A или B = B или A доказательство (естественный вычет)

Question

A или B = B или A доказательство (естественный вычет)

Эта проблема кажется, что это должно быть проще, чем я сделал, поэтому мой главный вопрос будет: есть ли более простой способ сделать это? По логике мы знаем, что

A v B = B v A

Но при естественном выводе мы используем наши v-интродукции, RAA и т. Д., Чтобы доказать эти эквивалентности. В процессе решения практической задачи я столкнулся с необходимостью доказать это коммутативное свойство, но нахожу его на удивление трудным. Мне кажется, что доказательство начнется так:

1. A v B            given
2.     ¬(B v A)     assume
3.     ¬B ^ ¬A      2, deMorgan's
4.     ¬A           3, ^-elimination
5.     ¬B           3, ^-elimination
6.     ¬A ^ ¬B      4, 5, ^-I
7.     ¬(A v B)     6, deMorgan's
?. B v A            2, 7 RAA

И теперь мы находимся в положении, в котором мы должны доказать де Моргана. Нет ли более простого доказательства для A v B = B v A?

2

logic commutativity

Источник

user5789075 24 апр '16 в 10:47

3 ответа

Другие вопросы по тегам logic commutativity

user1199624 24 апр '16 в 11:12 2016-04-24 11:12 · Answer 1 · 2016-04-24 11:12

Вы можете создавать настоящие таблицы и сравнивать их

 A    | B     | A v B
true  | true  | true
true  | false | true
false | true  | true
false | false | false


 A    | B     | B v A
true  | true  | true
true  | false | true
false | true  | true
false | false | false

Таблицы равны, выражения равны.

3

Источник

user1199624 24 апр '16 в 11:12

user1793332 26 апр '16 в 01:43 2016-04-26 01:43 · Answer 2 · 2016-04-26 01:43

Не решая всю проблему для вас, попробуйте этот подход:

Assume A
Prove that A => (BvA)
Assume B
Prove that B => (BvA)
So (AvB) => (BvA)     [That's v-intro, at least it is in Lemon's system which you appear to be using]

You've been given AvB. So modus ponens gives you BvA.

2

Источник

user1793332 26 апр '16 в 01:43

user6055422 21 ноя '18 в 01:17 2018-11-21 01:17 · Answer 3 · 2018-11-21 01:17

В следующем доказательстве использовалась проверка Клемента. Дополнительную информацию можно найти в тексте forallx. Ссылки на оба ниже.

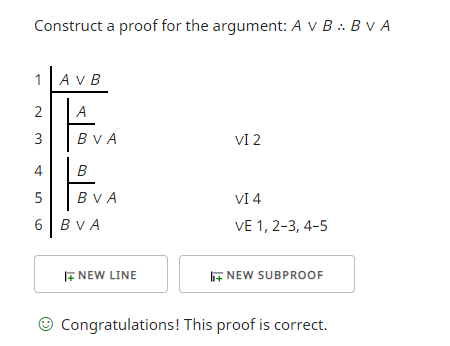
Введение дизъюнкции (∨I) позволяет перестроить дизъюнкцию в другом порядке.

Первый завершает доказательство последней строкой, используя устранение дизъюнкции (∨E), ссылаясь на саму дизъюнкцию (строка 1), первое дизъюнктное субстойкое (строки 2-3) достигает желаемого результата, а второе дизъюнктное субстекло (строки 4-5) поступает на желаемый результат.

Рекомендации

Редактор и средство проверки естественных дедукций Кевина Клемента в стиле JavaScript/PHP Fitch http://proofs.openlogicproject.org/

П.Д. Магнус, Тим Баттон с дополнениями Дж. Роберта Лофтиса, ремикс и рецензия Аарона Томаса-Болдука, Ричарда Зака, forallx Калгари Ремикс: Введение в формальную логику, зима 2018. http://forallx.openlogicproject.org/