Вывод в байесовской сети, построение дерева соединений

Question

Предполагая, что вы знаете дерево соединений байесовской сети (чтобы построить вручную для простых примеров), напишите на Python программу для распространения убеждений, чтобы вычислить условные вероятности P(Q|e) для произвольных Q ∈ U и e ⊂ U. Мне следует использовать алгоритм дерева соединений.

Это код, который я смог написать. Кто-нибудь может мне помочь? Я знаю теорию этой проблемы, но не знаю, как ее реализовать.

      network = {
    'flu': {'prob': 0.05},
    'cough': {'prob': 0.1, 'parents': ['flu']},
    'fever': {'prob': 0.3, 'parents': ['flu']},
    'fatigue': {'prob': 0.2, 'parents': ['flu']}
}

moralized_graph = {}
for node in network:
    moralized_graph[node] = set(network[node].get('parents', []))
for node1 in network:
    for node2 in moralized_graph[node1]:
        moralized_graph[node2].add(node1)


flu_prob = {"flu": {0: 0.95, 1: 0.05}}
cough_prob = {"cough": {0: 0.9, 1: 0.1}, "flu": {0: {0: 0.6, 1: 0.4}, 1: {0: 0.8, 1: 0.2}}}
fever_prob = {"fever": {0: 0.7, 1: 0.3}, "flu": {0: {0: 0.8, 1: 0.2}, 1: {0: 0.5, 1: 0.5}}}
fatigue_prob = {"fatigue": {0: 0.8, 1: 0.2}, "flu": {0: {0: 0.7, 1: 0.3}, 1: {0: 0.6, 1: 0.4}}}

potential_1 = {(0, 0): flu_prob["flu"][0] * cough_prob["flu"][0][0],
               (0, 1): flu_prob["flu"][0] * cough_prob["flu"][0][1],
               (1, 0): flu_prob["flu"][1] * cough_prob["flu"][1][0],
               (1, 1): flu_prob["flu"][1] * cough_prob["flu"][1][1]}
potential_2 = {(0, 0): flu_prob["flu"][0] * fever_prob["flu"][0][0],
               (0, 1): flu_prob["flu"][0] * fever_prob["flu"][0][1],
               (1, 0): flu_prob["flu"][1] * fever_prob["flu"][1][0],
               (1, 1): flu_prob["flu"][1] * fever_prob["flu"][1][1]}
potential_3 = {(0, 0): flu_prob["flu"][0] * fatigue_prob["flu"][0][0],
               (0, 1): flu_prob["flu"][0] * fatigue_prob["flu"][0][1],
               (1, 0): flu_prob["flu"][1] * fatigue_prob["flu"][1][0],
               (1, 1): flu_prob["flu"][1] * fatigue_prob["flu"][1][1]}

class JunctionTree:
    def __init__(self, clusters, edges):
        self.clusters = clusters
        self.edges = edges
        
junction_tree_clusters = [
    (["flue", "fatigue"], potential_1),
    (["flue", "fever"], potential_2),
    (["flue", "cough"], potential_3),
]

junction_tree_edges = [
    (["flue", "fatigue"], ["flue", "fever"]),
    (["flue", "fever"], ["cough", "flue"]),
]

junction_tree = JunctionTree(junction_tree_clusters, junction_tree_edges)

graph = {"flu": ["cough",fever", "fatigue"], "cough": [], "fever": [], "fatigue": []}

Answer 1

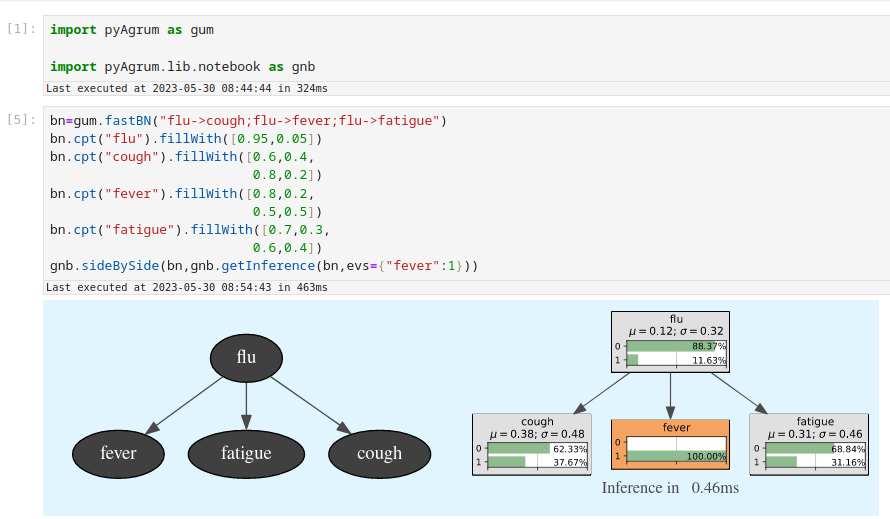
используя pyAgrum и для этого BN и этого вывода:

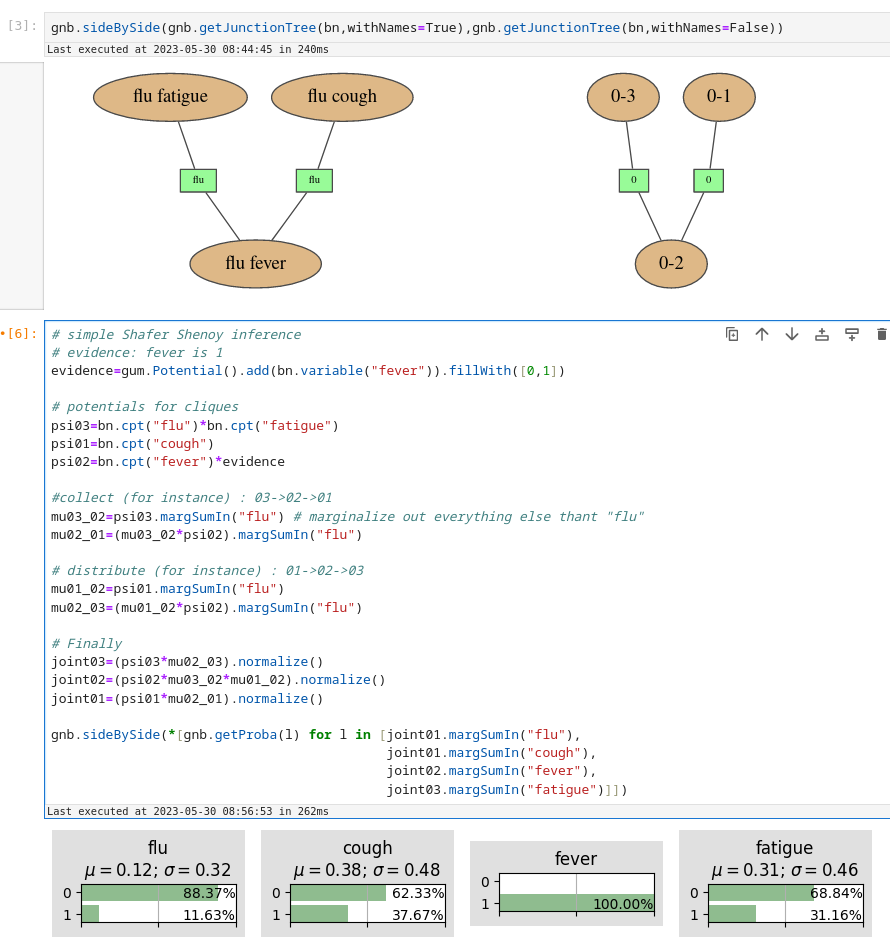
Вот код этого вывода. Это можно легко обобщить (и оптимизировать).

      # evidence: fever is 1
evidence=gum.Potential().add(bn.variable("fever")).fillWith([0,1])

# potentials for cliques
psi03=bn.cpt("flu")*bn.cpt("fatigue")
psi01=bn.cpt("cough")
psi02=bn.cpt("fever")*evidence

#collect (for instance) : 03->02->01
mu03_02=psi03.margSumIn("flu") # marginalize out everything else thant "flu"
mu02_01=(mu03_02*psi02).margSumIn("flu")

# distribute (for instance) : 01->02->03
mu01_02=psi01.margSumIn("flu")
mu02_03=(mu01_02*psi02).margSumIn("flu")

# Finally
joint03=(psi03*mu02_03).normalize()
joint02=(psi02*mu03_02*mu01_02).normalize()
joint01=(psi01*mu02_01).normalize()