Степень давления в зависимости от трения и других геометрических факторов

Question

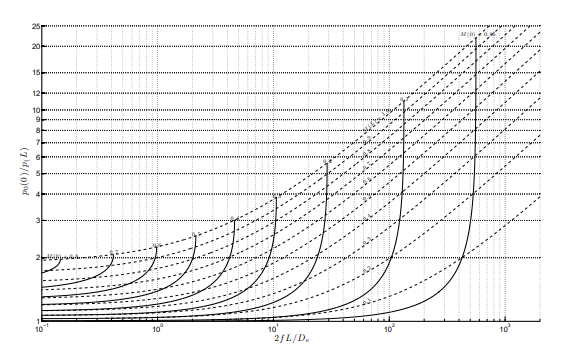
Проблема, с которой я столкнулся, состоит в построении графика, который я прикрепляю, на данный момент только прерывистых линий.

.

Для этого мне нужно принять во внимание эти уравнения:

.

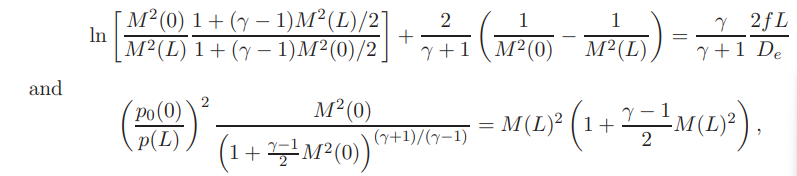Прежде чем приступить к объяснению процесса, отметим одну константу, гамма=1,4, которую я собираюсь использовать.

Чтобы начать строить график, я беру уравнение 1. Я беру значения M(L) от 0,1 до 1 и «x» (x=2fL/De) от 10e-1 до 10e3 (непрерывным способом), как вы можете видеть. в графике. Отсюда все, что я делаю, это получаю значение M(0) для каждого значения M(L), чтобы позже у меня было 10 разных кривых.

Как только у меня есть все значения M(0), я перехожу ко второму уравнению и, вводя значения M(0) и M(L), получаю соответствующие значения соотношения давлений (P0(0)/P(L))--> ось Y.

По причине, которую я не могу объяснить, когда я запрашиваю у Chatgpt код Python, я получаю следующий код, скопированный ниже, с соответствующим графиком, и кривые не совпадают с кривыми на изображении 1. Я извлек непосредственно латексный код с помощью Mathpix из уравнений, задействованных в chatgpt, для преобразования его в код Python, и таким образом я гарантирую, что он правильно пишет уравнения.

Может ли кто-нибудь помочь мне найти правильное решение моей проблемы?

Код:

      import numpy as np
import matplotlib.pyplot as plt

# Function to solve for M(0) given M(L)
def solve_M0(M_L):
    y = np.log((x**2 / M_L**2) * (1 + (gamma - 1) * M_L**2 / 2) /
               (1 + (gamma - 1) * x**2 / 2)) + 2 / (gamma + 1) * (1 / x**2 - 1 / M_L**2)
    return np.exp(y)
    
# Function to solve for p0(0)/p(L) given M(0)
def solve_p_ratio(M_0):
    y = (M_0**2 / (1 + (gamma - 1) / 2 * M_0**2)**((gamma + 1) / (gamma - 1))) * x**2 / (1 + (gamma - 1) / 2 * x**2)
    return np.sqrt(y)

# Plotting
M_L_values = np.arange(0.1, 1.1, 0.1)  # Values of M_L
x = np.linspace(1e-1, 1e3, 1000)  # Values for x-axis (2*f*L/De)
# Constants
gamma = 1.4

plt.figure(figsize=(10, 6))
for M_L in M_L_values:
    M_0 = solve_M0(M_L)
    p_ratio = solve_p_ratio(M_0)
    plt.plot(x, p_ratio, label=f'M_L = {M_L}')

plt.xlabel('2*f*L/De')
plt.ylabel('p0(0)/p(L)')
plt.xscale('log')
plt.legend()
plt.grid(True)
plt.title('Plot of p0(0)/p(L) vs 2*f*L/De for different M_L values')
plt.show()

Затем я попробовал идти шаг за шагом, сначала вычисляя связь между M(0) и x. Я очистил значение M(0), как на изображении 2 [изображение 2][1][1]: https://i.stack.imgur.com/D0pwT.png

Я получил код, выполняющий численный расчет методом Якоби, следующим образом:

      import matplotlib.pyplot as plt

def jacobi_method(ML, x):
    gamma = 1.4
    tol = 1e-6
    max_iter = 100

    M0_prev = 1.0  # Valor inicial para M(0)
    M0 = M0_prev

    for _ in range(max_iter):
        M0 = np.sqrt(ML **2 * (1 + (gamma - 1) / 2 * M0 **2 * 
        np.exp(gamma / (gamma + 1) * x) * np.exp(-2 * (ML**2 - M0**2) / 
        (M0**2 * ML**2 * (gamma + 1))))) / (1 + (gamma - 1) / 2 * ML**2)
        
        if np.abs(M0 - M0_prev) < tol:
            break

        M0_prev = M0

    return M0

ML_values = [0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0]
x_values = np.logspace(-1, 2, num=1000)

M0_values = np.zeros((len(ML_values), len(x_values)))

for i, ML in enumerate(ML_values):
    for j, x in enumerate(x_values):
        M0_values[i, j] = jacobi_method(ML, x)

plt.figure(figsize=(10, 6))
plt.xlabel('x')
plt.ylabel('M(0)')

for i, ML in enumerate(ML_values):
    plt.plot(x_values, M0_values[i, :], label=f'M(L) = {ML}')

plt.legend()
plt.grid(True)
plt.show()

I am getting some errors regarding "overflow encountered in scalar multiply" and "invalid value encountered in scalar divide" plus some of the results I get for M0 are NaN and there should be 1000 values for M0 since there are 1000 values of x, which is not my case. Im pretty sure that my equation is right, but maybe I am not using the method properly