Что такое стабильность в алгоритмах сортировки и почему это важно?
Мне очень любопытно, почему стабильность является или не важна в алгоритмах сортировки?
9 ответов
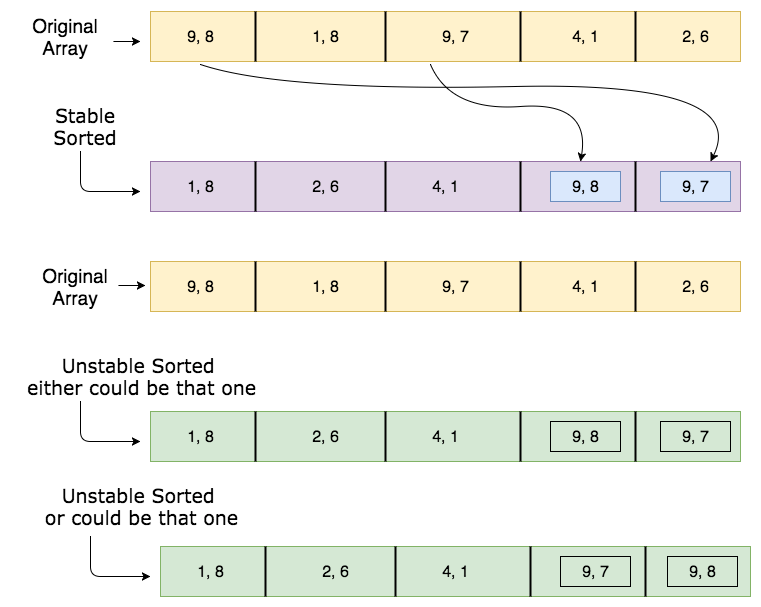
Алгоритм сортировки называется стабильным, если два объекта с одинаковыми ключами отображаются в одинаковом порядке в отсортированном выводе так же, как они появляются во входном массиве для сортировки. Некоторые алгоритмы сортировки по своей природе стабильны, такие как сортировка вставками, сортировка слиянием, сортировка по пузырям и т. Д. А некоторые алгоритмы сортировки не являются такими, как сортировка по кучи, быстрая сортировка и т.д.
Предыстория: "стабильный" алгоритм сортировки сохраняет элементы с одинаковым ключом сортировки в порядке. Предположим, у нас есть список из 5 букв:
peach
straw
apple
spork
Если мы отсортируем список только по первой букве каждого слова, тогда будет получена стабильная сортировка:
apple
peach
straw
spork
В нестабильном алгоритме сортировки, straw или же spork могут быть взаимозаменяемыми, но в стабильном они остаются в одинаковых относительных позициях (то есть, так как straw появляется раньше spork на входе, он также появляется перед spork в выходной).
Мы могли бы отсортировать список слов, используя этот алгоритм: стабильная сортировка по столбцу 5, затем 4, затем 3, затем 2, затем 1. В конце концов, он будет правильно отсортирован. Убедите себя в этом. (кстати, этот алгоритм называется радикальной сортировкой)
Теперь, чтобы ответить на ваш вопрос, предположим, у нас есть список имен и фамилий. Нас просят отсортировать "по фамилии, потом по имени". Мы могли бы сначала отсортировать (стабильный или нестабильный) по имени, затем стабильную сортировку по фамилии. После этих сортировок список в первую очередь сортируется по фамилии. Однако, если фамилии совпадают, имена сортируются.
Вы не можете сложить нестабильные сортировки таким же образом.
Алгоритм стабильной сортировки - это алгоритм, который сортирует идентичные элементы в том же порядке, в котором они отображаются на входе, тогда как нестабильная сортировка может не соответствовать случаю.
Стабильные алгоритмы сортировки:
- Сортировка вставки
- Сортировка слиянием
- Пузырьковая сортировка
- Тим Сорт
- Подсчет Сортировка
Нестабильные алгоритмы сортировки:
- Сортировка кучи
- Сортировка выбора
- Оболочка сортировки
- Быстрая сортировка
Стабильность сортировки означает, что записи с одним и тем же ключом сохраняют свой относительный порядок до и после сортировки.
Таким образом, стабильность имеет значение тогда и только тогда, когда проблема, которую вы решаете, требует сохранения этого относительного порядка.
Если вам не нужна стабильность, вы можете использовать быстрый алгоритм загрузки памяти из библиотеки, такой как heapsort или quicksort, и забыть об этом.
Если вам нужна стабильность, это сложнее. Стабильные алгоритмы имеют более высокую загрузку ЦП и / или памяти, чем нестабильные алгоритмы. Поэтому, когда у вас большой набор данных, вы должны выбирать между биением процессора или памяти. Если вы ограничены как процессором, так и памятью, у вас есть проблема. Хороший компромиссный устойчивый алгоритм - это сортировка двоичного дерева; статья в Википедии содержит патетически простую реализацию C++, основанную на STL.
Вы можете превратить нестабильный алгоритм в стабильный, добавив исходный номер записи в качестве ключа последнего места для каждой записи.
Это зависит от того, что вы делаете.
Представьте, что у вас есть записи о людях с полями имени и фамилии. Сначала вы сортируете список по имени. Если вы затем отсортируете список с помощью стабильного алгоритма по фамилии, у вас будет список, отсортированный по имени и фамилии.
Есть несколько причин, почему стабильность может быть важна. Во-первых, если две записи не нужно менять местами, вы можете вызвать обновление памяти, страница помечается как грязная и должна быть перезаписана на диск (или другой медленный носитель).
Алгоритм сортировки называется стабильным, если два объекта с одинаковыми ключами появляются в одинаковом порядке в отсортированном выводе, как они появляются во входном несортированном массиве. Некоторые алгоритмы сортировки по своей природе стабильны, такие как сортировка вставками, сортировка слиянием, сортировка по пузырям и т. Д. А некоторые алгоритмы сортировки не являются такими, как сортировка по кучи, быстрая сортировка и т. Д.
Однако любой данный алгоритм сортировки, который не является стабильным, может быть модифицирован для обеспечения стабильности. Могут существовать отдельные способы сортировки, чтобы сделать его стабильным, но в целом любой алгоритм сортировки, основанный на сравнении, который не является стабильным по своей природе, может быть изменен для обеспечения стабильности путем изменения операции сравнения ключей, так что сравнение двух ключей рассматривает положение как фактор для объектов с равными ключами.
Ссылки: http://www.math.uic.edu/~leon/cs-mcs401-s08/handouts/stability.pdf http://en.wikipedia.org/wiki/Sorting_algorithm
Я знаю, что есть много ответов на этот вопрос, но для меня этот ответ sgwill резюмировал это гораздо яснее:
Стабильная сортировка - это та, которая сохраняет исходный порядок входного набора, где алгоритм [unstable] не различает два или более элементов.
Еще несколько примеров того, почему нужны стабильные сорта. Базы данных - типичный пример. Возьмем, к примеру, базу данных транзакций, которая включает в себя фамилию | имя, дату | время покупки, номер позиции, цену. Скажем, база данных обычно сортируется по дате | времени. Затем выполняется запрос для создания отсортированной копии базы данных по | фамилии | имени, поскольку стабильная сортировка сохраняет исходный порядок, даже если сравнение запроса включает только | фамилию, транзакции для каждой | фамилии | имени будут быть в порядке данных | времени.
Похожим примером является классический Excel, который ограничивал сортировку до 3 столбцов за раз. Чтобы отсортировать 6 столбцов, выполняется сортировка по 3 наименее значимым столбцам, за которыми следует сортировка с 3 наиболее значимыми столбцами.
Классическим примером стабильной сортировки по системе счисления является сортировщик карточек, используемый для сортировки по полю из десяти числовых столбцов. Карточки отсортированы от младшего разряда к старшему разряду. На каждом проходе колода карт читается и разделяется на 10 различных ячеек в соответствии с цифрой в этом столбце. Затем 10 лотков с картами возвращаются в приемный лоток по порядку (сначала "0" карт, затем "9" карт). Затем выполняется еще один проход к следующему столбцу, пока все столбцы не будут отсортированы. Фактические сортировщики карт имеют более 10 ячеек, так как на карте 12 зон, столбец может быть пустым и есть ячейка для неверного считывания. Для сортировки букв необходимо 2 прохода на столбец, 1-й проход для цифры, 2-й проход для зоны 12 11.
Позже (1937 г.) появились машины для сопоставления (слияния) карт, которые могли объединять две колоды карт путем сравнения полей. На входе были две уже отсортированные колоды карт, основная колода и колода обновления. Подборщик объединил две колоды в новую корзину для материалов и корзину для архива, которая дополнительно использовалась для основных дубликатов, так что в новой главной корзине будут только карты обновлений в случае дубликатов. Вероятно, это было основой идеи первоначальной (восходящей) сортировки слиянием.
Если вы предполагаете, что сортируете только цифры, и только их значения идентифицируют / различают их (например, элементы с одинаковыми значениями идентичны), тогда проблема стабильности сортировки не имеет смысла.
Однако объекты с одинаковым приоритетом в сортировке могут различаться, и иногда их относительный порядок представляет собой значимую информацию. В этом случае нестабильная сортировка порождает проблемы.
Например, у вас есть список данных, который содержит затраты времени [T] всех игроков на очистку лабиринта с уровнем [L] в игре. Предположим, нам нужно оценить игроков по скорости очистки лабиринта. Однако применяется дополнительное правило: игроки, которые чистят лабиринт с более высоким уровнем, всегда имеют более высокий ранг, независимо от того, сколько времени стоит.
Конечно, вы можете попытаться отобразить парное значение [T,L] на действительное число [R] с помощью некоторого алгоритма, который следует правилам, а затем ранжировать всех игроков со значением [R].
Однако, если стабильная сортировка возможна, тогда вы можете просто отсортировать весь список по [T] (сначала более быстрые игроки), а затем по [L]. В этом случае относительный порядок игроков (по стоимости времени) не изменится после того, как вы сгруппируете их по уровню лабиринта, который они убрали.
PS: конечно, подход к сортировке дважды - не лучшее решение конкретной проблемы, но для объяснения вопроса об афише этого должно быть достаточно.
Стабильная сортировка всегда будет возвращать одно и то же решение (перестановку) на одном входе.
Например, [2,1,2] будет отсортировано с использованием стабильной сортировки в качестве перестановки [2,1,3] (сначала это индекс 2, затем индекс 1, затем индекс 3 в отсортированном выводе). Это означает, что выходные данные всегда перетасовываются одинаково. Другой нестабильной, но все же правильной перестановкой является [2,3,1].
Быстрая сортировка не является стабильной сортировкой, и различия в перестановках между одинаковыми элементами зависят от алгоритма выбора сводной точки. Некоторые реализации выбирают случайным образом, и это может сделать быструю сортировку, приводящую к разным перестановкам на одном входе с использованием одного и того же алгоритма.
Алгоритм стабильной сортировки необходим детерминистически.