Как сгладить цифровой сигнал, базовая линия которого прыгает вверх и вниз с помощью Python?

Question

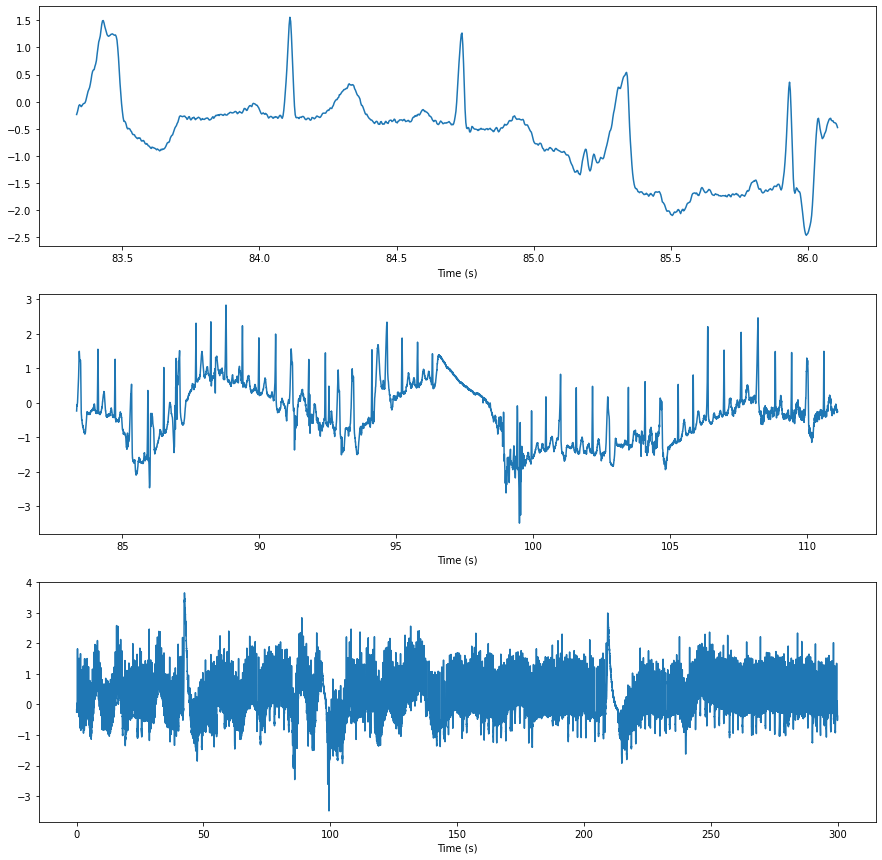
Я анализирую встроенный набор данных электрокардиограммы (ЭКГ) из SciPy, часть которого выглядит следующим образом: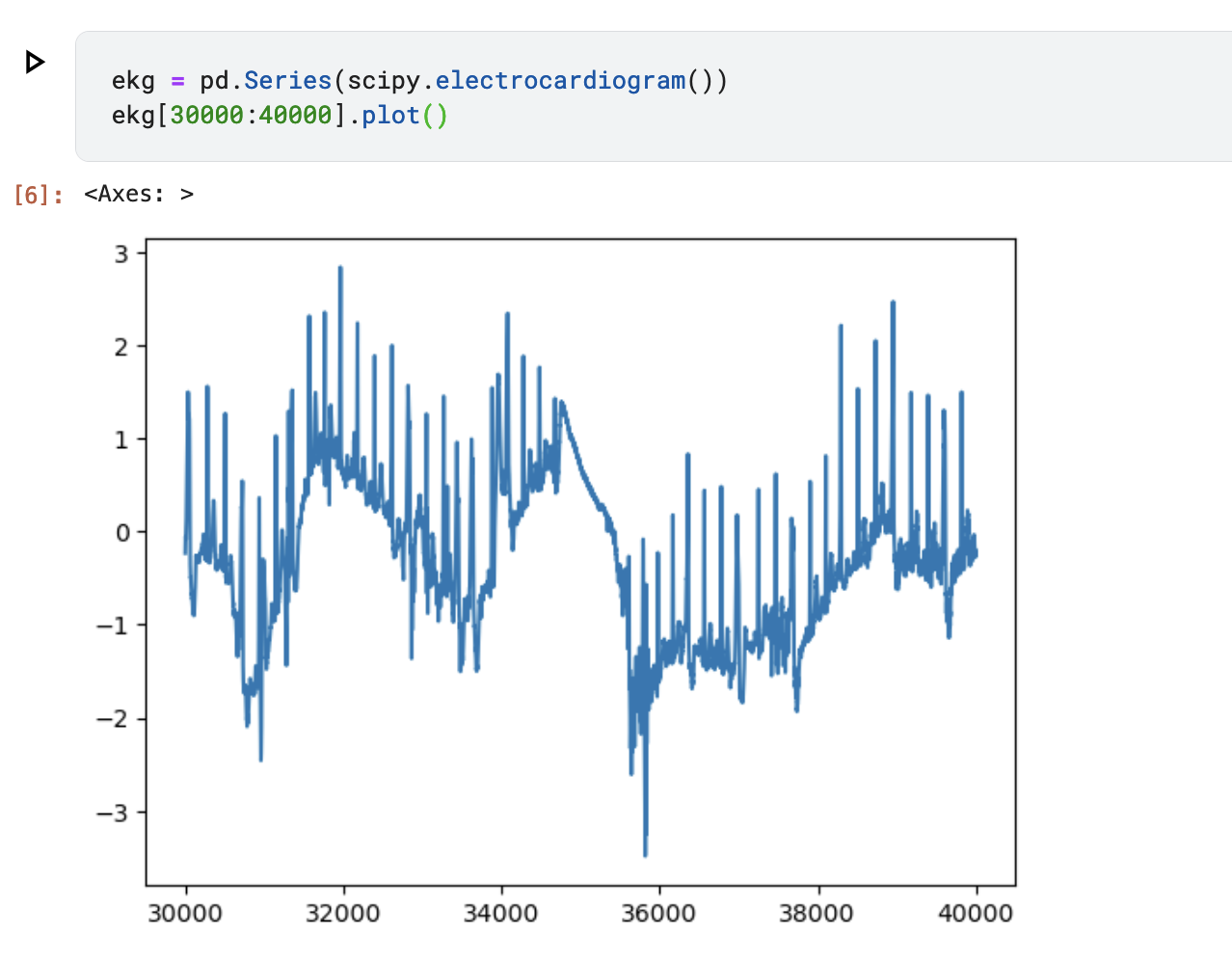

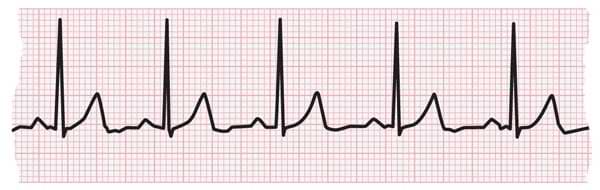
Одна из проблем с приведенными выше данными заключается в том, что базовая линия ЭКГ сильно подскакивает вверх и вниз. Если вы не знакомы с ЭКГ или анализом сердцебиения, они должны быть плоскими с несколькими пиками «комплекса QRS» (также известного как фактическое сердцебиение), как показано ниже:

Компании по производству медицинского оборудования, производящие мониторы ЭКГ, используют некоторые функции выравнивания и фильтрации, чтобы сделать ЭКГ более плавными и легкими для чтения, поскольку естественные движения человеческого тела неизбежны и приводят к скачкам сигнала ЭКГ, как показано выше. Но я не знаю, какие фильтры/функции они используют.

Как я могу использовать SciPy или написать собственную функцию для выравнивания набора данных ЭКГ SciPy, приведенного выше?

Что я пробовал

Я пробовал читать документацию SciPy по обработке сигналов , но пока не нашел никаких функций, которые «сглаживают» данные или приводят их к базовому состоянию. Я новичок в обработке цифровых сигналов и хочу знать, есть ли лучший или официальный способ сделать это.

Я пробовал смещать значения вверх или вниз с помощью некоторой скользящей средней, но простое сложение или вычитание значений Y не является правильным способом. Это слишком хакерски.

Спасибо за вашу помощь.

Уточнение вопроса: исправление «блуждания базовой линии»

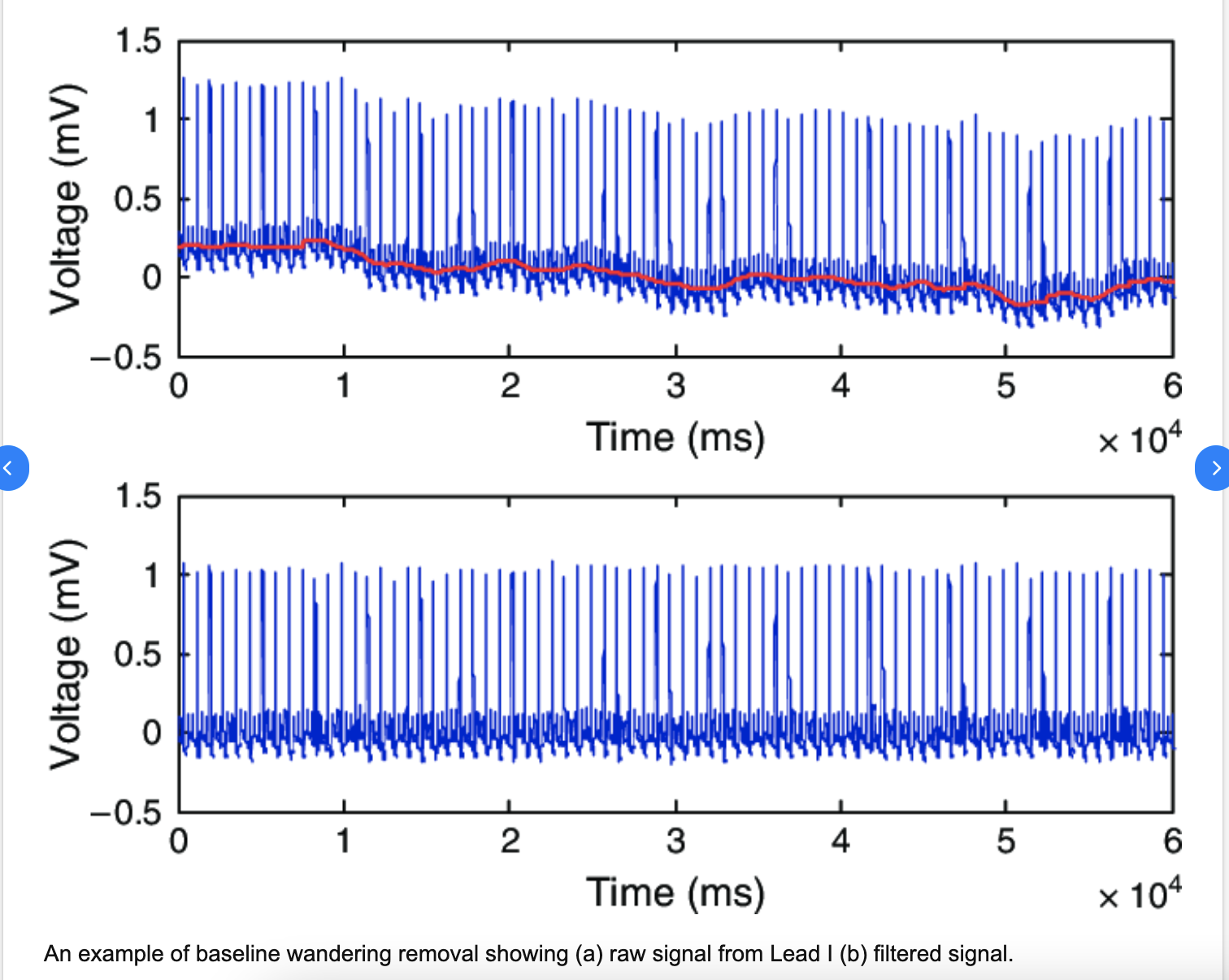
Другой пользователь в комментариях (Кристоф Раквитц) предложил фильтр верхних частот. Гугля по фильтрам верхних частот, я нашел изображение из исследовательской работы по ЭКГ :

Они сказали, что первое изображение имело «смещение базовой линии», и именно на это я и пытаюсь ответить этим вопросом. Как исправить смещение базовой линии?

Две полезные исследовательские статьи

Учитывая исследовательскую работу, о которой я упоминал в последнем разделе, а также еще одну, которую я только что нашел, об исправлении отклонения базовой линии на ЭКГ , я прочитаю их и посмотрю, что найду.

Answer 1

Вот демонстрация некоторых фильтров нижних частот.

Вам захочется прочитать о «причинных» фильтрах и непричинных фильтрах, а также о разнице между FIR и IIR.

Загрузка данных:

      signal = scipy.datasets.electrocardiogram()
fs = 360 # say the docs
time = np.arange(signal.size) / fs # for plotting only

Исследуйте сигнал:

      fig, axs = plt.subplots(3, 1, figsize=(15, 15))
axs[0].plot(time[30000:31000], signal[30000:31000])
axs[1].plot(time[30000:40000], signal[30000:40000])
axs[2].plot(time, signal)
axs[0].set_xlabel('Time (s)')
axs[1].set_xlabel('Time (s)')
axs[2].set_xlabel('Time (s)')
plt.show()

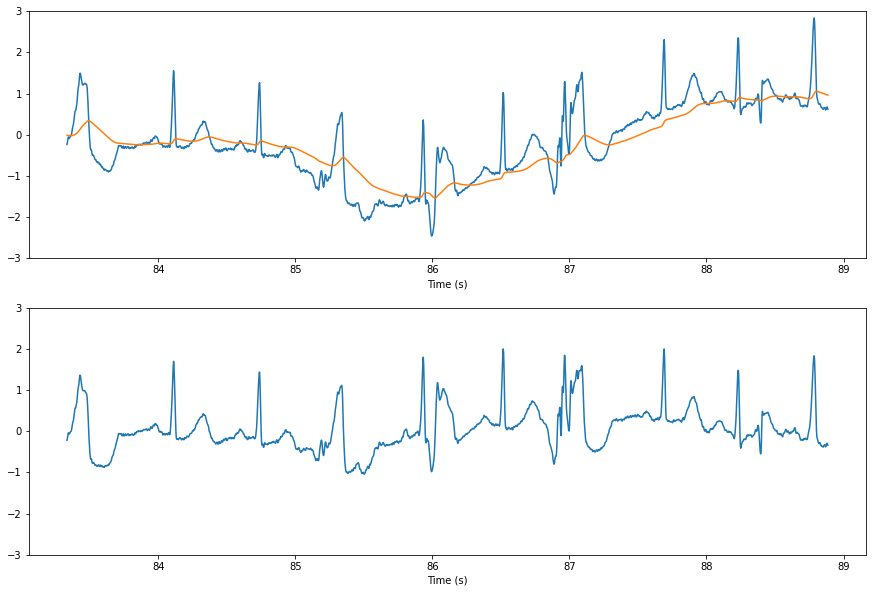
Пробую несколько фильтров:

      # Butterworth, first order, 0.5 Hz cutoff
lowpass = scipy.signal.butter(1, 0.5, btype='lowpass', fs=fs, output='sos')
lowpassed = scipy.signal.sosfilt(lowpass, signal)
highpassed = signal - lowpassed

fig, axs = plt.subplots(2, 1, figsize=(15, 10))
axs[0].plot(time[30000:32000], signal[30000:32000])
axs[0].plot(time[30000:32000], lowpassed[30000:32000])
axs[1].plot(time[30000:32000], highpassed[30000:32000])
axs[0].set_xlabel('Time (s)')
axs[1].set_xlabel('Time (s)')
axs[0].set_ylim([-3, +3])
axs[1].set_ylim([-3, +3])
plt.show()

      # take note of these coefficients:
>>> scipy.signal.butter(1, 0.5, btype='lowpass', fs=fs, output='ba')
(array([0.00434, 0.00434]), array([ 1.     , -0.99131]))
# and compare to the following...

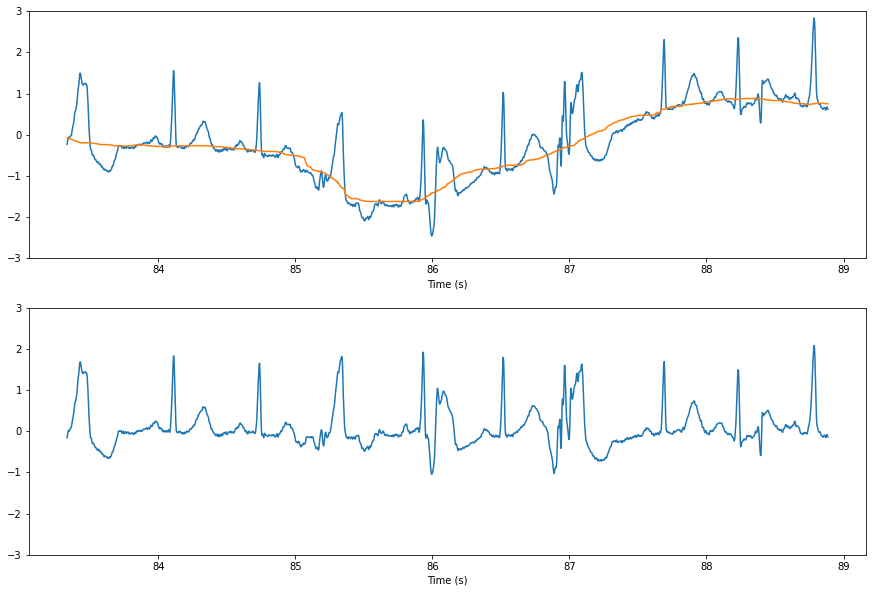
      # Almost the same thing, different formulation: "exponential average"
# y += (x - y) * alpha  # applied to each value X of the signal to produce a new Y

alpha = 1/100 # depends on fs and desired cutoff frequency
lowpassed = scipy.signal.lfilter([alpha], [1, -(1-alpha)], signal)
highpassed = signal - lowpassed

fig, axs = plt.subplots(2, 1, figsize=(15, 10))
axs[0].plot(time[30000:32000], signal[30000:32000])
axs[0].plot(time[30000:32000], lowpassed[30000:32000])
axs[1].plot(time[30000:32000], highpassed[30000:32000])
axs[0].set_xlabel('Time (s)')
axs[1].set_xlabel('Time (s)')
axs[0].set_ylim([-3, +3])
axs[1].set_ylim([-3, +3])
plt.show()

      # the first two filters were "causal", i.e. only using past samples.
# downside: lag, phase shift, i.e. the lowpass doesn't quite match/track the signal.
# "non-causal" filters can use future samples.
# this allows to remove the phase shift but the processing introduces a delay instead.
# this delay is irrelevant for offline processing or if it's considered "small enough".
# the following are non-causal.

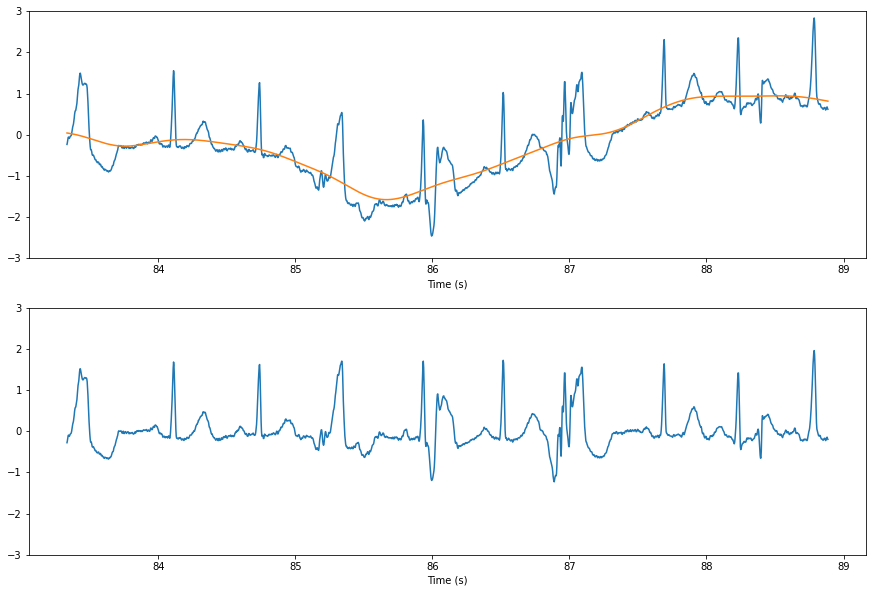
      # median filter. interpret peaks as outliers, so this reveals whatever can be considered "baseline".
# can be causal if the kernel window only covers the past but that introduces lag (noticeable when the signal drifts actively).
# might need another pass of smoothing, on the median filter, before subtracting.
# median filtering CAN be cheap, if using the right data structure. scipy implementation seems less smart, takes noticeable time.

lowpassed = scipy.signal.medfilt(signal, kernel_size=fs+1)
highpassed = signal - lowpassed

fig, axs = plt.subplots(2, 1, figsize=(15, 10))
axs[0].plot(time[30000:32000], signal[30000:32000])
axs[0].plot(time[30000:32000], lowpassed[30000:32000])
axs[1].plot(time[30000:32000], highpassed[30000:32000])
axs[0].set_xlabel('Time (s)')
axs[1].set_xlabel('Time (s)')
axs[0].set_ylim([-3, +3])
axs[1].set_ylim([-3, +3])
plt.show()

      lowpassed = scipy.ndimage.gaussian_filter1d(signal, sigma=0.2 * fs, order=0)
highpassed = signal - lowpassed

fig, axs = plt.subplots(2, 1, figsize=(15, 10))
axs[0].plot(time[30000:32000], signal[30000:32000])
axs[0].plot(time[30000:32000], lowpassed[30000:32000])
axs[1].plot(time[30000:32000], highpassed[30000:32000])
axs[0].set_xlabel('Time (s)')
axs[1].set_xlabel('Time (s)')
axs[0].set_ylim([-3, +3])
axs[1].set_ylim([-3, +3])
plt.show()

Answer 2

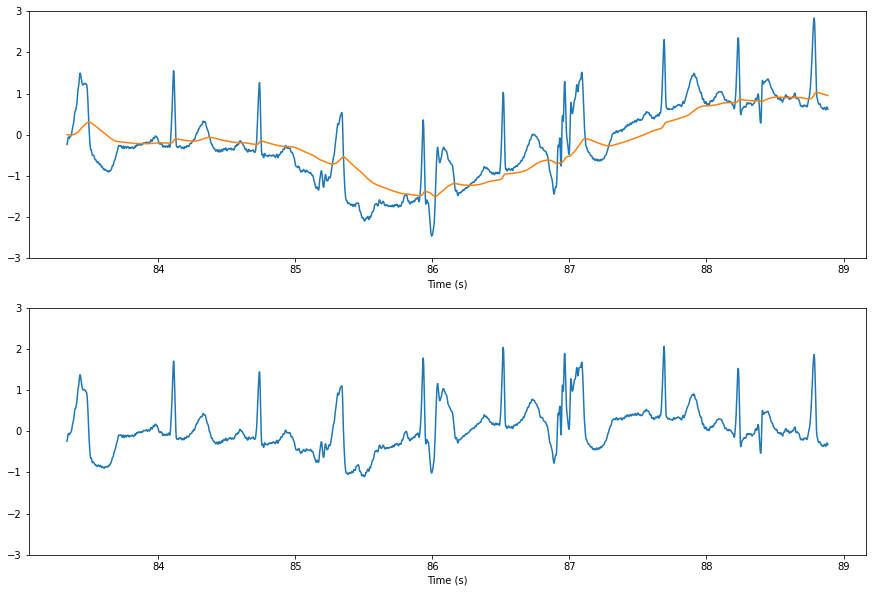
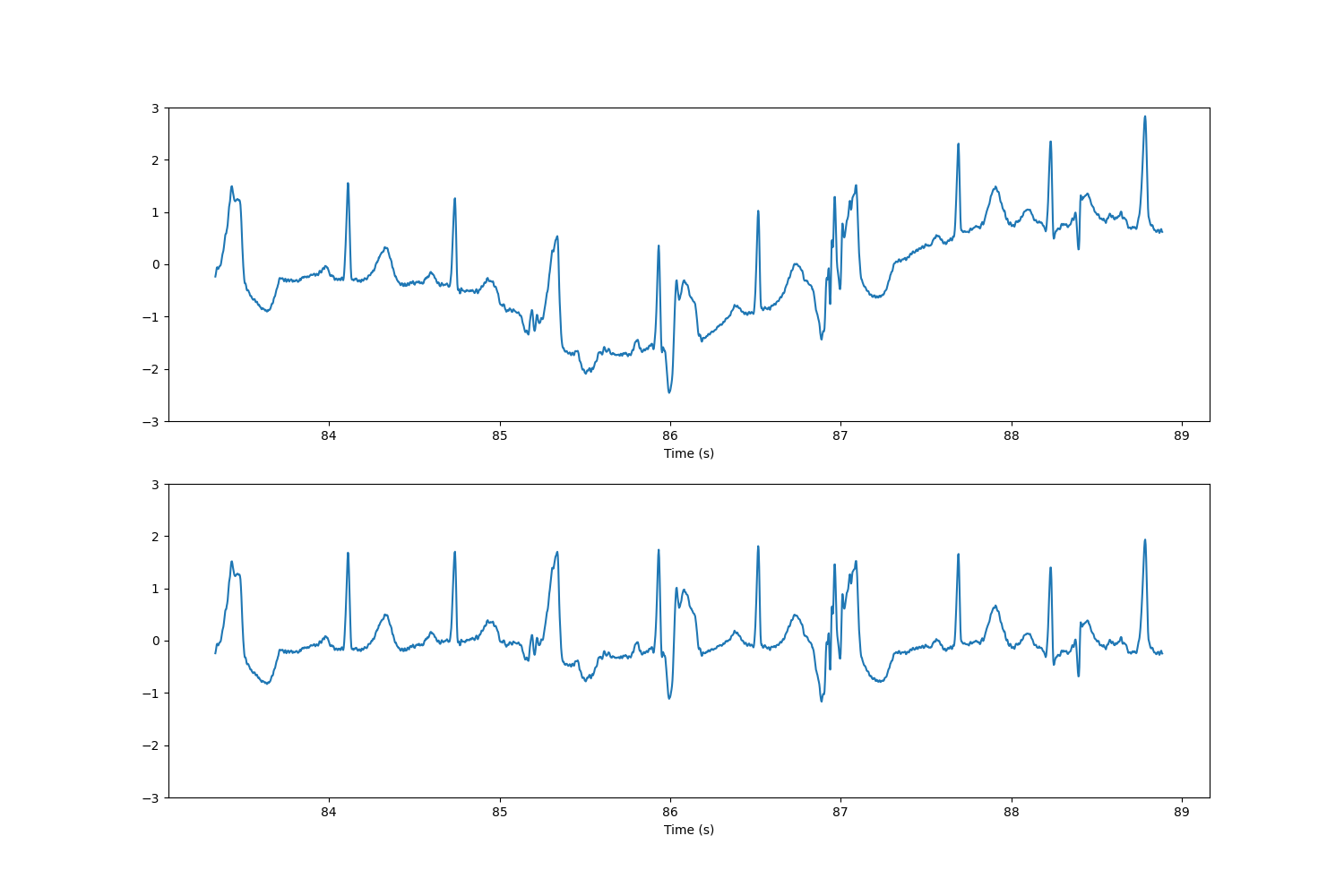
Чтобы добавить к довольно обширному ответу Кристофа Раквица (из которого я взял код построения графика), вы также можете использовать непричинный (сохраняющий фазу) БИХ-фильтр верхних частот, чтобы удалить дрейф базовой линии. По сути, это то же самое, что использовать фильтр нижних частот для вычисления движущейся базовой линии и последующего вычитания ее из исходного сигнала:

      from scipy import signal, datasets
import matplotlib.pyplot as plt
import numpy as np

ecg = datasets.electrocardiogram()
fs = 360 
time = np.arange(ecg.size) / fs 
[b,a] = signal.butter(4, 0.5, btype='highpass', fs=fs)
filtered = signal.filtfilt(b, a, ecg)

fig, axs = plt.subplots(2, 1, figsize=(15, 10))
axs[0].plot(time[30000:32000], ecg[30000:32000])
axs[1].plot(time[30000:32000], filtered[30000:32000])
axs[0].set_xlabel('Time (s)')
axs[1].set_xlabel('Time (s)')
axs[0].set_ylim([-3, +3])
axs[1].set_ylim([-3, +3])
plt.show()

Обязательно используйтеfiltfiltи неfilt(или разновидность типаsosfilt), иначе нелинейная фазовая характеристика БИХ-фильтра (например, фильтра Баттерворта) изменит форму вашего сигнала и, возможно, испортит дальнейший анализ QRS. КИХ-фильтр не сделает этого, но он также сместит ваш исходный сигнал во времени на столько выборок, сколько у вас есть коэффициентов фильтра, которых будет много (до 400+) для хорошей плотной частотной характеристики.