Идеальная реконструкция вейвлет-преобразования с использованием CWT

Question

Если я выполняю стандартное вейвлет-преобразование, а затем выполняю обратное, я ожидал получить исходный сигнал:

% dummy series:
Fs = 1e3;
t = 0:1/Fs:1;
x = exp(cos(2*pi*32*t).*(t>=0.1 & t<0.3) + sin(2*pi*64*t).*(t>0.7));

% perform default transform and inverse
wt=cwt(x)
rx=icwt(wt)

% plot
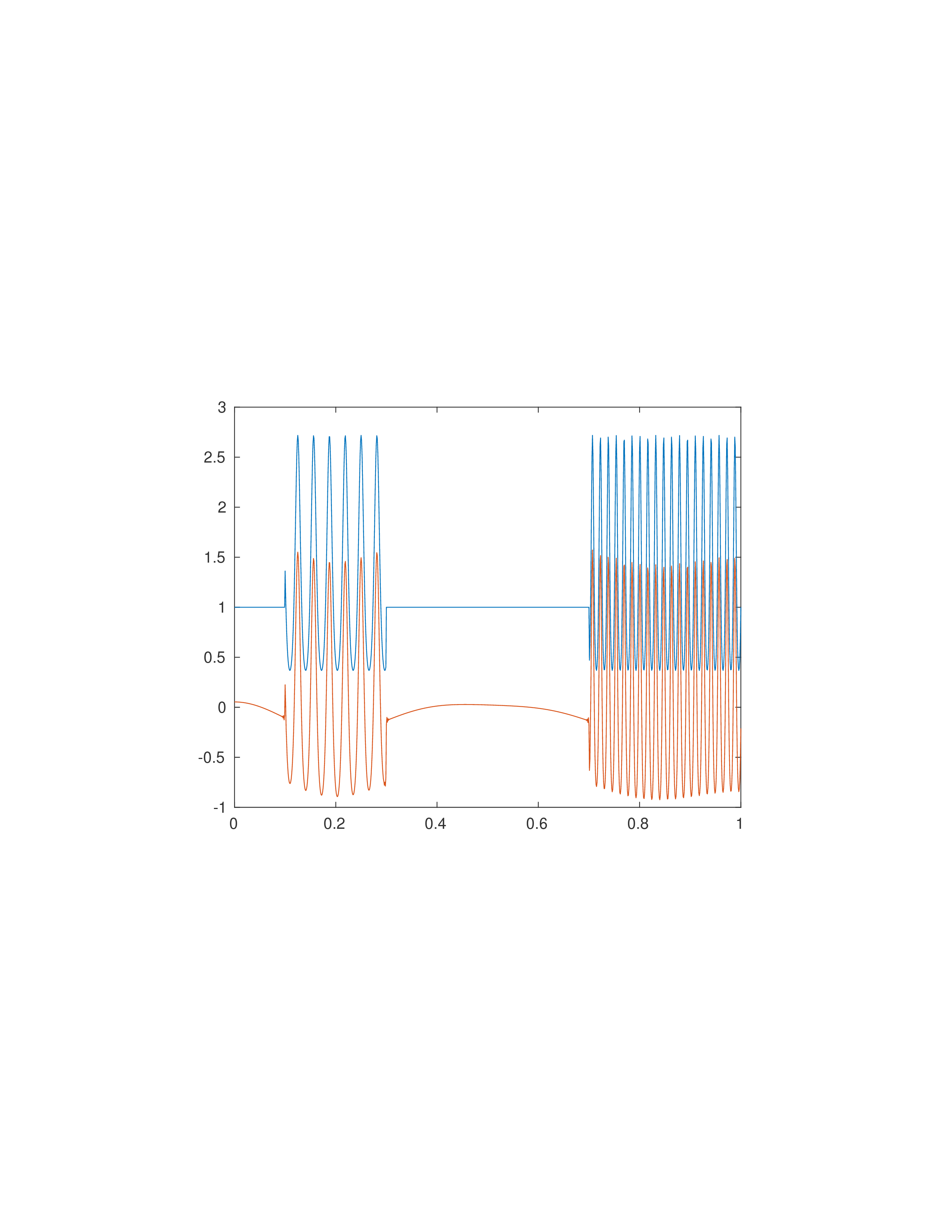
plot(t,x,t,rx)

Помимо смещения, сигналы плоского периода искажены.
Кажется, что возможно выполнить преобразование / инверсию и иметь что-то, близкое к тождественной функции, как здесь вейвлет-реконструкция временного ряда R, но, читая учебные пособия / справку для cwt, я не вижу, как этого добиться.

Answer 1

Документация Matlab объясняет, что CWT - не лучший выбор для идеальной реконструкции. Однако, если вы хотите сравнить разные полосы как сигналы с тем же размером, что и оригинал, вы можете использовать MODWT (или инвариантный к сдвигу DWT с помощью циклического вращения, иногда вызываемого по кругу).