Что правильно по здравому смыслу: (int) blabla * 255.99999999999997 или круглый (blabla*255)?

Question

Недавно в источниках webkit я обнаружил эту интересную вещь, связанную с преобразованием цветов (hsl в rgb):

http://osxr.org/android/source/external/webkit/Source/WebCore/platform/graphics/Color.cpp#0111

const double scaleFactor = nextafter(256.0, 0.0); // it's here something like 255.99999999999997
// .. some code skipped
return makeRGBA(static_cast<int>(calcSomethingFrom0To1(blablabla) * scaleFactor), 

То же самое я нашел здесь: http://www.filewatcher.com/p/kdegraphics-4.6.0.tar.bz2.5101406/kdegraphics-4.6.0/kolourpaint/imagelib/effects/kpEffectHSV.cpp.html

(int)(value * 255.999999)

Правильно ли вообще использовать такую ​​технику? Почему бы не использовать что-то прямое, например, круглое (блабла * 255)? Это особенности C/C++? Как я вижу, строго говоря, это вернет не всегда правильные результаты, в 27 случаях из 100. См. Электронную таблицу по адресу https://docs.google.com/spreadsheets/d/1AbGnRgSp_5FCKAeNrELPJ5j9zON9HLiHoHC870PwdMc/edit?usp=sharing

Кто-нибудь, пожалуйста, объясните - я думаю, что это должно быть что-то основное.

Answer 1

Обычно мы хотим отобразить реальное значение x в (закрытом) интервале [0,1] в целочисленное значение j В диапазоне [0 ...255],

И мы хотим сделать это "честным" способом, чтобы, если действительные значения были равномерно распределены в диапазоне, дискретные значения были приблизительно равновероятны: каждое из 256 дискретных значений должно иметь "одинаковую долю" (1/256) из [0,1] интервал. То есть нам нужно отображение, подобное этому:

[0    , 1/256) -> 0
[1/256, 2/256) -> 1 
...
[254/256, 255/256) -> 254
[255/256, 1]       -> 255

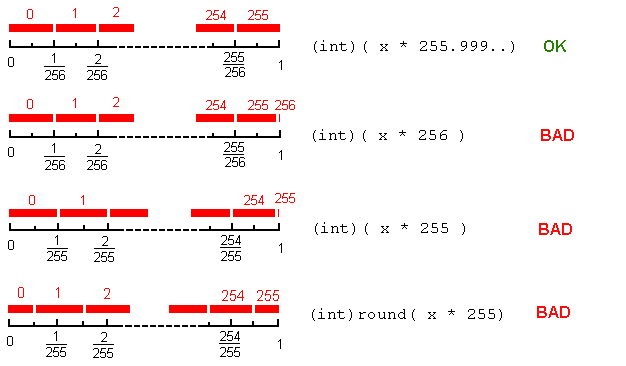
Нас не очень заботят точки перехода [*], но мы хотим охватить весь диапазон [0,1]. Как это сделать?

Если мы просто делаем j = (int)(x *255): значение 255 почти никогда не появится (только когда x=1); и остальные ценности 0...254 каждый получил бы долю 1/255 интервала. Это было бы несправедливо, независимо от поведения округления в предельных точках.

Если мы вместо этого делаем j = (int)(x * 256): этот раздел будет справедливым, за исключением проблемы sngle: мы получим значение 256 (вне диапазона!), когда x=1 [**]

Вот почему j = (int)(x * 255.9999...) (где 255.9999... на самом деле самый большой двойной меньше, чем 256) будет делать.

Альтернативная реализация (также разумная, почти эквивалентная) будет

j = (int)(x * 256); 
if(j == 256)  j = 255;  
// j = x == 1.0 ? 255 : (int)(x * 256); // alternative

но это было бы более неуклюжим и, вероятно, менее эффективным.

round() здесь не помогает Например, j = (int)round(x * 255) даст 1/255 долю целым числам j=1...254 и половина этого значения до крайних точек j=0, j=255,

[*] Я имею в виду: нас не очень интересует, что происходит в "маленьком" районе, скажем, 3/256: округление может дать 2 или 3, это не имеет значения. Но нас интересуют экстремумы: мы хотим получить 0 и 255, для x=0 а также x=1соответственно.

[**] Стандарт IEEE с плавающей запятой гарантирует, что здесь нет неопределенности округления: целые числа допускают точное представление с плавающей запятой, произведение будет точным, а приведение будет всегда 256. Далее, мы гарантируем, что 1.0 * z = z,

Answer 2

В общем скажу (int)(blabla * 255.99999999999997) правильнее использовать round(),

Зачем?

Потому что с round(), 0 и 255 имеют только "половину" диапазона, который делают 1-254. если ты round()затем 0-0.00196078431 сопоставляются с 0, а 0,00196078431-0.00588235293 сопоставляются с 1. Это означает, что 1 имеет на 200% больше вероятности возникновения, чем 0, что, строго говоря, является несправедливым смещением.

Если вместо этого один умножается на 255,9999999999997, а затем на этажи (что делает приведение к целому числу, так как оно усекается), то каждое целое число от 0 до 255 одинаково вероятно.

Ваша электронная таблица могла бы показать это лучше, если бы она учитывалась в долях в процентах (то есть, если она учитывалась каждый раз по 0,01% вместо 1%). Я сделал простую таблицу, чтобы показать это. Если вы посмотрите на эту таблицу, то увидите, что 0 несправедливо round()но с другим методом все справедливо и одинаково.

Answer 3

Приведение к типу int имеет тот же эффект, что и функция floor (т.е. оно усекается). Когда вы звоните вокруг него, ну, округляет до ближайшего целого числа.

Они делают разные вещи, поэтому выберите тот, который вам нужен.