Октавная ошибка: несоответствие горизонтальных размеров - матричная поэлементная матрица

Question

k = linspace(0,0.5)'
h = 6.58212 * 10^-16

m_0 = 9.109383 * 10^-31
E_c = ( h^2 * k.^2 ) / ( 10^-5 * m_0 )
A = [E_c, 1, 2; 3, 4, 5; 6, 7, 8]

Когда я запускаю этот код, я получаю:

error: horizontal dimensions mismatch (100x1 vs 1x1)
error: called from
    physics at line 42 column 3

Я хотел бы рассчитать собственные значения. Но для этого нужно сначала иметь матрицу, которая не падает. Я понимаю, что E_c - это вектор размером 100x1, который я пытаюсь вставить в первый слот матрицы A 3x3, и этот слот имеет размер 1x1. Нужно ли использовать поэлементно, чтобы сделать это?

Мы хотим найти значения собственных значений, где один из элементов матрицы является функцией.

Answer 1

Вот некоторые возможности, я добавил tic/toc для измерения времени выполнения.

k = linspace(0,0.5)';

h = 6.58212 * 10^-16;   
m_0 = 9.109383 * 10^-31;
E_c = ( h^2 * k.^2 ) / ( 10^-5 * m_0 );

%% method 1
%% arrayfun, no explicit loop, explicit calculation
tic
ev1 = arrayfun(@(x)eig([x 1 2; 3 4 5; 6 7 8]), E_c', 'unif', false);
ev1 = cell2mat(ev1);
toc

%% method 2
%% arrayfun, no explicit loop, function handle
tic
funEigA = @(x)eig([x 1 2; 3 4 5; 6 7 8]);
ev2 = arrayfun(funEigA, E_c', 'unif', false);
ev2 = cell2mat(ev2);
toc

%% method 3
%% explicit loop, with pre allocation of matrix, explicit calculation, no function handle in loop
tic
ev3 = zeros(length(funEigA(0)),length(E_c)); % evaluate funEigA to determin the number of eigen values. In this case this is 3, because it's a 3x3 matrix.
for ik = 1:length(E_c)
    ev3(:,ik) = eig([E_c(ik) 1 2; 3 4 5; 6 7 8]);
end
toc

%% method 4
%% with pre allocation of matrix, explicit loop & call of function handle
tic
ev4 = zeros(length(funEigA(0)),length(E_c));
for ik = 1:length(E_c)
    ev4(:,ik) = funEigA(E_c(ik));
end
toc

%% method 5
%% without pre allocation, explicit loop, call of function handle
tic
ev5 = [];
for val = E_c' % k must be a column vector
    ev5(:,end+1) = funEigA(val);
end
toc

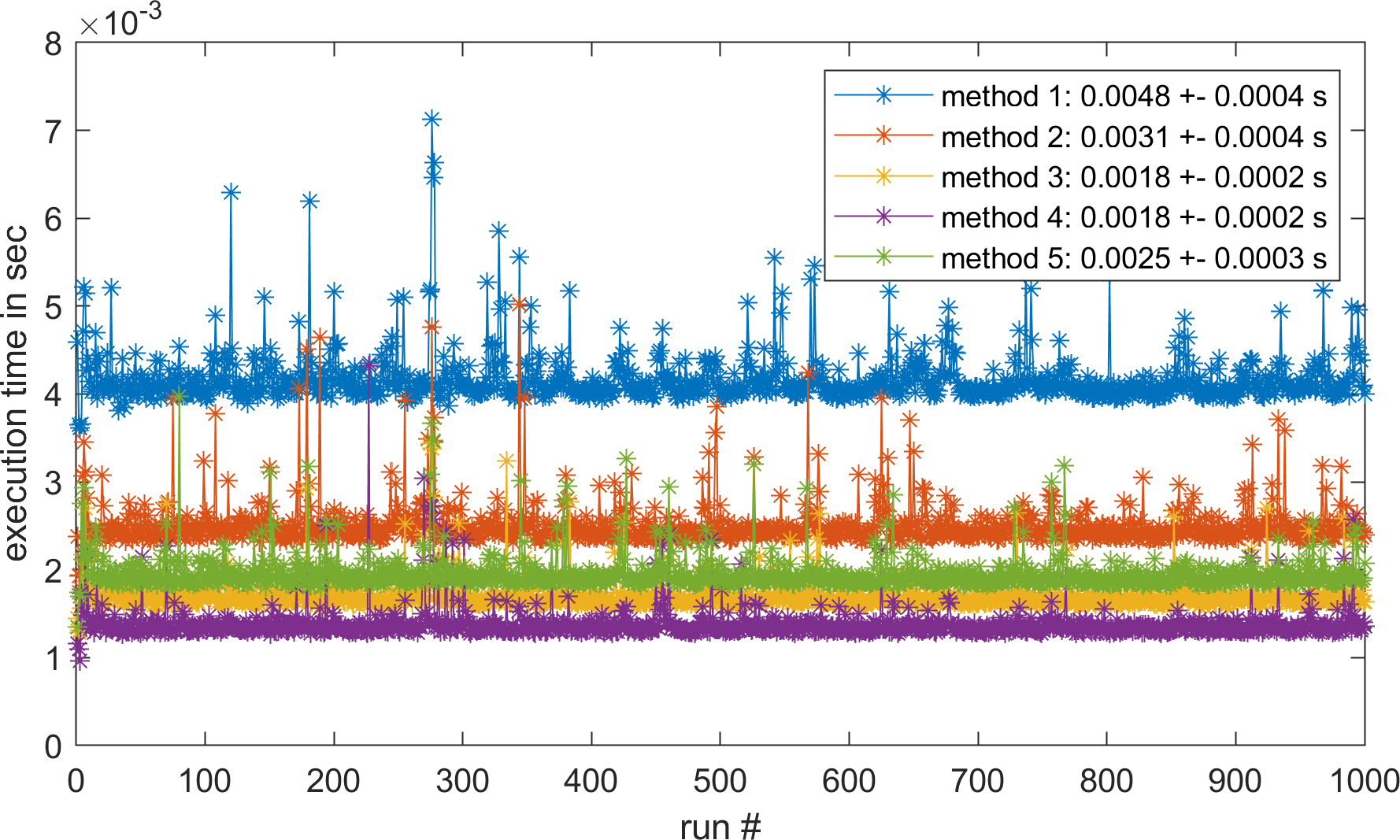
Если вы заинтересованы в производительности каждого метода, вот мой вывод (Lenovo T450, Core i7, 3,2 ГГц):

Elapsed time is 0.010564 seconds.
Elapsed time is 0.007659 seconds.
Elapsed time is 0.008660 seconds.
Elapsed time is 0.008498 seconds.
Elapsed time is 0.009461 seconds.

Или после 1000 прогонов:

Лично мне нравится метод № 1 и № 2, потому что он короткий и понятный, что происходит. Но на самом деле они медленнее и для больших k или больших матриц использование массивов ячеек может стать даже намного менее производительным, чем использование предварительно выделенных матриц.

Если вы хотите измерить скорость выполнения несколько раз, убедитесь, что вы используете clear all заранее, иначе результаты могут быть кэшированы.