Путаница относительно представления с плавающей запятой

Question

Я читал статью доктора Уильяма Т. Вертса под названием « 8-битное представление с плавающей запятой», где автор определяет, как следует из названия, 8-битное представление с плавающей запятой с одним битом для знака, тремя битами для экспоненты и оставшиеся четыре бита для мантиссы.

Вопрос 1

Теперь в статье он пишет:

Диапазон допустимых показателей степени (представляющих ни денормализованные, ни бесконечные числа) тогда находится между 2^{-2} и 2^{+3}.

Я не понимаю, что он имеет в виду под юридическим в данном контексте. И почему 2^{-3} не может быть "законным" значением? Как и при смещении 2^{-3} на 3, получается 0, который находится в поле экспоненты.

вопрос 2

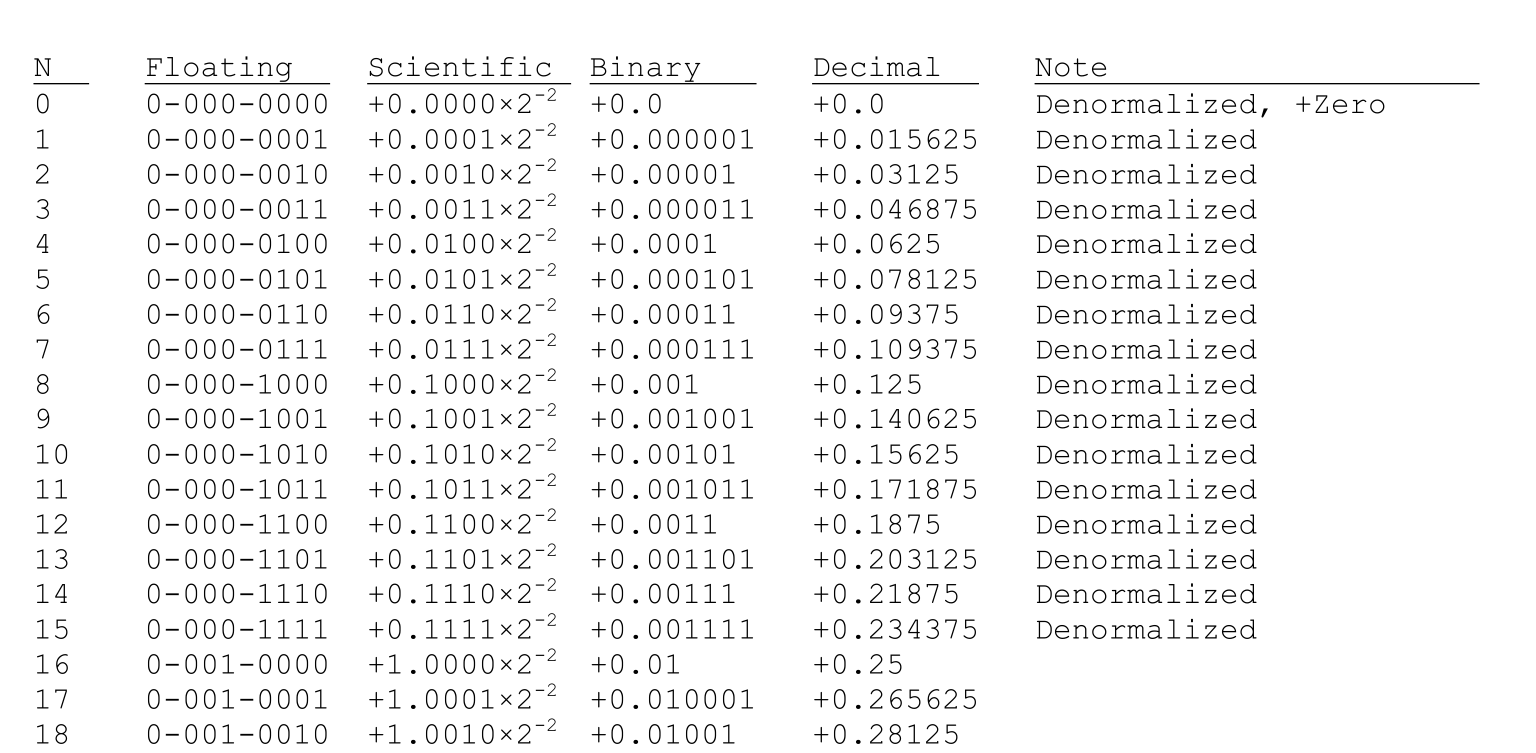
Далее он перечисляет все возможные значения чисел, представимых в этой системе. Я прикрепляю скриншот первых нескольких денормализованных чисел ниже.

Я понимаю, что мы не можем представлять малые числа в нормализованном виде, что вынуждает нас отходить от нормы и использовать0перед запятой, а не обычно1, что дает нам то, что мы называем денормализованной формой.

Но почему мы используем-2в показателе2(скорее, чем-3)?

Согласно правилам экспоненты-3, поле экспоненты должно иметь -2+3=1, которое находится в поле экспоненты, но вместо этого оно имеет поле экспоненты (у него есть001в нормированных числах). Но, если мы используем2^{-3}, поле экспоненты действительно должно иметь -3+3=0.

Хороший итог моего второго вопроса: почему мы не используем 2^{-3} в качестве показателя степени от N=1 до N=15? Поле экспоненты имеет000что соответствует -3 в качестве показателя степени.

Примечание. Я понимаю, что природа самой темы довольно запутана. Таким образом, если в моем вопросе есть неясность, прошу указать на нее в комментариях.

Answer 1

Но почему мы используем-2в показателе2(скорее, чем-3)?

Предположим, вы сделали это. С полем степени 000 ₂ для субнормальных чисел (ведущий бит 0) и значениями поля первичной мантиссы ¹ от 0000 ₂ до 1111 ₂ можно представить числа от 0,0000 ₂ •2⁻³ до 0,1111 ₂ •2⁻³ . А с полем экспоненты 001 ₂ для нормальных чисел (начальный бит 1) и значениями поля первичной мантиссы от 0000 ₂ до 1111 ₂ можно представить числа от 1,0000 ₂ •2 ⁻² до 1,1111 ₂ •2 ⁻² .

Где находится 1,0000 ₂ •2⁻³ ? Субнормаль останавливается на 0,1111 ₂ •2⁻³ , а нормали начинаются на 1,0000 ₂ •2 ⁻² . Все числа от 1,0000 ₂ •2⁻³ до 1,1111 ₂ •2⁻³ были пропущены.

Когда вы идете вниз от самой низкой субнормальной величины, 1,0000 ₂ •2⁻², вы не можете одновременно уменьшить показатель степени и изменить начальную цифру с 1 на 0.

Вот почему код экспоненты 000 ₂ означает тот же код экспоненты, что и 001 ₂ . Это код для изменения начального бита на 0, но с использованием того же показателя степени, что и самые низкие нормали. Что также отвечает на ваш первый вопрос.

Поле экспоненты на самом деле кодирует как экспоненту, так и старший бит мантиссы:

Сноска

¹ «Значимый» — предпочтительный термин для дробной части числа с плавающей запятой. «Мантисса» — это старый термин для дробной части логарифма. Мантиссы логарифмические; добавление к мантиссе умножает число. Значения линейны; добавление к мантиссе добавляет к числу (в масштабе по показателю степени).