Отсчитывая задние ребра, чтобы получить число цилиндров в ориентированном графе

Question

Я писал код, чтобы получить все возможные циклы в ориентированном графе. Вот реализация, которая отслеживает задние фронты, и всякий раз, когда один задний фронт обнаруживается, она возвращает истину, если обнаружен один цикл. Я расширил это до следующего: вычислить все возможные задние ребра в дереве, количество задних ребер должно дать количество циклов. Не уверен, что это правильно. используя это, я реализовал следующее: count Переменная ниже не полезна. Первоначально мне нужно было подсчитать каждый цикл. но это не дает правильного ответа. но размер edgeMap который хранит все задние грани, кажется, дает правильное количество циклов в некоторых графиках, но не во всех.

Код работает для G2 и G3 на рисунке, но не работает для G1. (G1 имеет только два цикла, но я получаю три задних ребра). любые предложения о том, где я могу пойти не так, будут полезны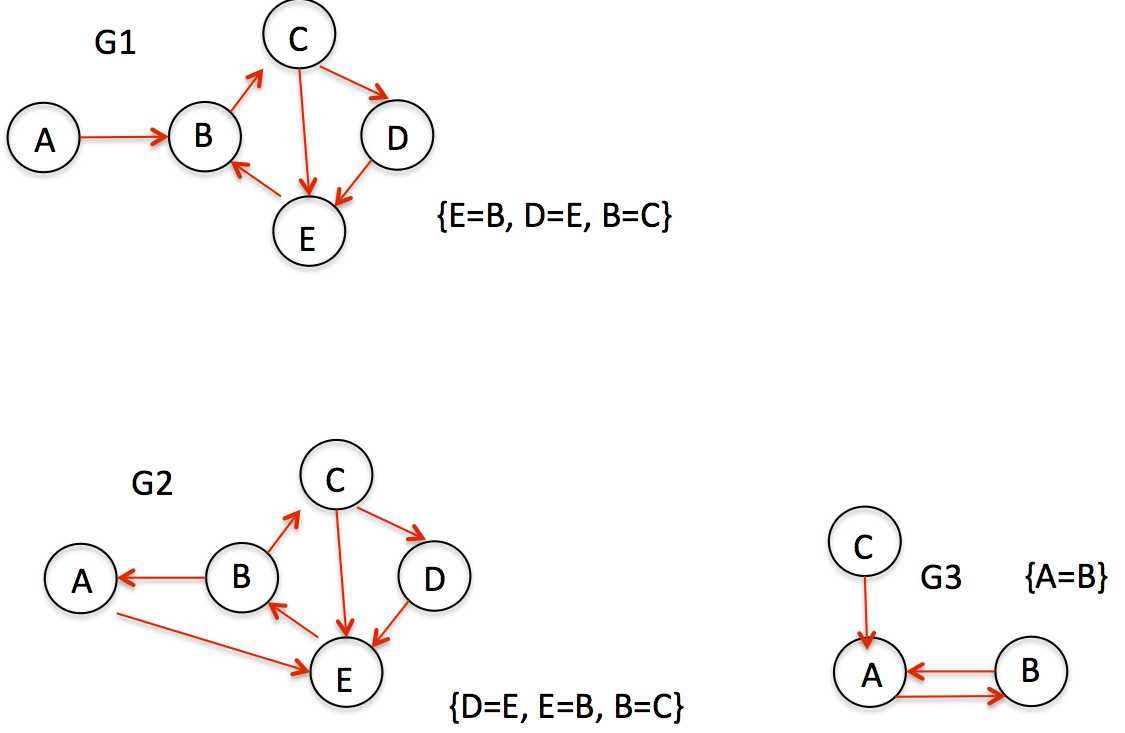

public int allCyclesDirectedmain(){
        clearAll();
        int count=0;
        Map<Vertex, Vertex> edgeMap = new HashMap<>();


        for (Vertex v : vertexMap.values()) {
            if (!v.isVisited && allCyclesDirected(v,edgeMap))
                count++;
        }
        System.out.println(edgeMap);
        return count;

    }
public boolean allCyclesDirected(Vertex v, Map<Vertex, Vertex> edgeMap ){
        if (!v.isVisited){
            v.setVisited(true);
            Iterator<Edge> e = v.adj.iterator();
            while (e.hasNext()){
                    Vertex t = e.next().target;
                    if (!t.isVisited && allCyclesDirected(t,edgeMap)){
                        edgeMap.put(v, t);
                            return true;
                    }
                    else 
                            return true;
                    }
                }
        return false;
    }

Answer 1

Количество задников не является числом циклов, поскольку один задний элемент может участвовать в нескольких циклах.

В вашем графике G1 давайте проследим прогресс поиска в глубину из A: он посещает A->B->C, а затем имеет выбор между D и E. Предположим, что это занимает D. Затем он посещает E, и находит один задний ход, идущий к B. Дело в том, что ребро EB участвует как в цикле BCE, так и в цикле BCDE!

Вот еще один пример: рассмотрим полный ориентированный граф на четырех узлах. Есть 12 ребер, но

• 6 двухвершинных циклов
• 8 трехвершинных циклов
• 6 четырехвершинных циклов

всего 20 циклов - больше, чем ребер на графике! Фактически, в графе может быть экспоненциальное количество циклов, и проблема их подсчета, называемая #CYCLE, не вычислима за полиномиальное время, если P! = NP.

Answer 2

Как упоминалось ранее, один задний элемент может вносить вклад в более чем один цикл, поэтому количество задних элементов не совпадает с числом циклов. Можно использовать алгоритм Джонсона, чтобы найти все простые циклы в графе.