Как преобразовать ядро в матричную нотацию?
Я пытаюсь понять алгоритм бикубической свертки и не смог понять, как ядро дано как кусочная функция,
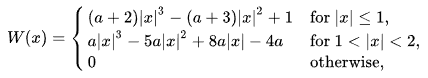
превращается в эту матрицу:
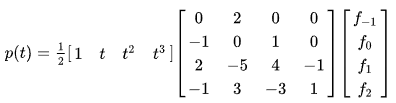
Я понимаю, что для получения матрицы а было установлено -0,5. Независимо от того, как я на это смотрю, я не могу прийти к показанной несимметричной матрице.
Я просмотрел статью Кейса, но он не расширился до матричной нотации, и я боролся с тем, как туда добраться.
Любое понимание будет высоко ценится.
2 ответа
Я нашел и понял, где Keys описывает процесс. Вы можете следовать сверху вниз на изображении ниже, но самый важный момент, который нужно отметить, это уравнение 7. 
Все значения в матрице получены из коэффициентов c-членов. Первая строка матрицы соответствует коэффициентам постоянных членов, а первый столбец соответствует элементам c_j-1. Это можно увидеть, сравнив приведенный ниже рисунок с коэффициентами уравнения 7: 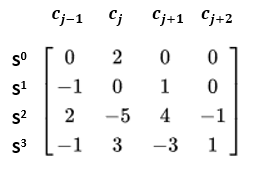
Я смог использовать это понимание для реализации метода кубической свертки для интерполяции поверхности, для которой мне удалось настроить значение a, чтобы увидеть ответ. Я рад помочь вам в этом, если что-то неясно!
Шаг 1, чтобы увидеть соотношение, состоит в умножении функции W(x) на выборочные входные данные f[n] для заданного сдвига t. Это дает 5 весов, умноженных на 5 входных выборок, и складываются вместе для формирования выходной выборки p(t).
Матрица, используемая для вычисления p (t), не является симметричной, поскольку для любого сдвига t, который не равен 0, веса, примененные к выборкам, также не являются симметричными. Вы можете увидеть это, написав W (t + i), которые являются весами, примененными к 5 выборкам вокруг выходной позиции t (i в [-2,2]).