Получение карты ориентации изображения отпечатка пальца с помощью OpenCV
Я пытаюсь реализовать метод улучшения изображения отпечатков пальцев от Анил Джейн. Для начала я столкнулся с некоторыми трудностями при извлечении изображения ориентации и строго следую инструкциям, описанным в разделе 2.4 этого документа.
Итак, это входное изображение:

И это после нормализации, используя тот же метод, что и в этой статье:

Я ожидаю увидеть что-то вроде этого (пример из интернета):

Однако вот что я получил за отображение полученной матрицы ориентации:

Очевидно, что это неправильно, и это также дает ненулевые значения для этих нулевых точек в исходном входном изображении.
Это код, который я написал:
cv::Mat orientation(cv::Mat inputImage)
{
cv::Mat orientationMat = cv::Mat::zeros(inputImage.size(), CV_8UC1);
// compute gradients at each pixel
cv::Mat grad_x, grad_y;
cv::Sobel(inputImage, grad_x, CV_16SC1, 1, 0, 3, 1, 0, cv::BORDER_DEFAULT);
cv::Sobel(inputImage, grad_y, CV_16SC1, 0, 1, 3, 1, 0, cv::BORDER_DEFAULT);
cv::Mat Vx, Vy, theta, lowPassX, lowPassY;
cv::Mat lowPassX2, lowPassY2;
Vx = cv::Mat::zeros(inputImage.size(), inputImage.type());
Vx.copyTo(Vy);
Vx.copyTo(theta);
Vx.copyTo(lowPassX);
Vx.copyTo(lowPassY);
Vx.copyTo(lowPassX2);
Vx.copyTo(lowPassY2);
// estimate the local orientation of each block
int blockSize = 16;
for(int i = blockSize/2; i < inputImage.rows - blockSize/2; i+=blockSize)
{
for(int j = blockSize / 2; j < inputImage.cols - blockSize/2; j+= blockSize)
{
float sum1 = 0.0;
float sum2 = 0.0;
for ( int u = i - blockSize/2; u < i + blockSize/2; u++)
{
for( int v = j - blockSize/2; v < j+blockSize/2; v++)
{
sum1 += grad_x.at<float>(u,v) * grad_y.at<float>(u,v);
sum2 += (grad_x.at<float>(u,v)*grad_x.at<float>(u,v)) * (grad_y.at<float>(u,v)*grad_y.at<float>(u,v));
}
}
Vx.at<float>(i,j) = sum1;
Vy.at<float>(i,j) = sum2;
double calc = 0.0;
if(sum1 != 0 && sum2 != 0)
{
calc = 0.5 * atan(Vy.at<float>(i,j) / Vx.at<float>(i,j));
}
theta.at<float>(i,j) = calc;
// Perform low-pass filtering
float angle = 2 * calc;
lowPassX.at<float>(i,j) = cos(angle * pi / 180);
lowPassY.at<float>(i,j) = sin(angle * pi / 180);
float sum3 = 0.0;
float sum4 = 0.0;
for(int u = -lowPassSize / 2; u < lowPassSize / 2; u++)
{
for(int v = -lowPassSize / 2; v < lowPassSize / 2; v++)
{
sum3 += inputImage.at<float>(u,v) * lowPassX.at<float>(i - u*lowPassSize, j - v * lowPassSize);
sum4 += inputImage.at<float>(u, v) * lowPassY.at<float>(i - u*lowPassSize, j - v * lowPassSize);
}
}
lowPassX2.at<float>(i,j) = sum3;
lowPassY2.at<float>(i,j) = sum4;
float calc2 = 0.0;
if(sum3 != 0 && sum4 != 0)
{
calc2 = 0.5 * atan(lowPassY2.at<float>(i, j) / lowPassX2.at<float>(i, j)) * 180 / pi;
}
orientationMat.at<float>(i,j) = calc2;
}
}
return orientationMat;
}
Я уже много искал в Интернете, но почти все они в Matlab. И очень мало кто использует OpenCV, но они мне тоже не помогли. Я искренне надеюсь, что кто-нибудь сможет просмотреть мой код и указать на любую ошибку, чтобы помочь. Заранее спасибо.
Обновить
Вот шаги, которые я следовал согласно статье:
- Получить нормализованное изображение Г.
- Разделите G на блоки размером wxw (16x16).
- Вычислить градиенты x и y в каждом пикселе (i,j).
Оцените локальную ориентацию каждого блока с центром в пикселях (i, j), используя уравнения:

Выполните фильтрацию нижних частот, чтобы удалить шум. Для этого преобразуйте изображение ориентации в непрерывное векторное поле, определенное как:

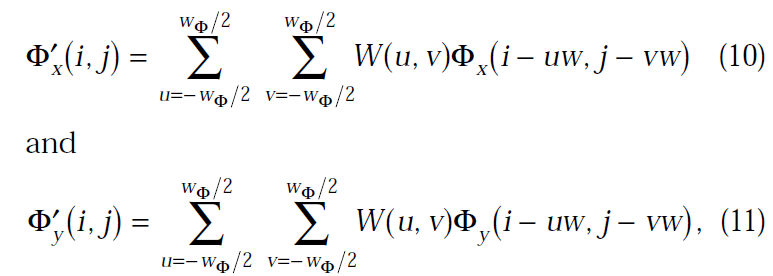
где W - двумерный фильтр нижних частот, а w(phi) x w(phi) - его размер, равный 5.
- Наконец, вычислите местную ориентацию гребня в (i, j), используя:

Update2
Это выходные данные Ориентации после изменения типа мата на CV_16SC1 в операции Собеля, как предложил Мика:

2 ответа
Может быть, мне уже поздно отвечать, но в любом случае кто-нибудь может прочитать это позже и решить ту же проблему.
Некоторое время я работал над тем же алгоритмом, тем же методом, который вы опубликовали... Но есть некоторые ошибки записи, когда папка была отредактирована (я полагаю). После многих испытаний с уравнениями я обнаружил эти ошибки, посмотрев другие подобные работы.
Вот что сработало для меня...
Vy(i, j) = 2*dx(u,v)*dy(u,v)
Vx(i,j) = dx(u,v)^2 - dy(u,v)^2
O(i,j) = 0.5*arctan(Vy(i,j)/Vx(i,j)
(Извините, я не смог опубликовать изображения, поэтому я написал измененные выражения. Remeber "u" и "v" - позиции суммирования по окну BlockSize by BlockSize)
Первым и самым важным (очевидно) являются уравнения, я видел, что в разных работах это выражение действительно было разным, и в каждом из них они говорили об одном и том же алгоритме Хонга и соавторов. Ключ находится в наименьшем среднем квадрате (первые 3 уравнения) градиентов (Vx и Vy), я предоставил исправленные формулы выше для этого действия. Затем вы можете вычислить угол тета для неперекрывающегося окна (размер 16x16, рекомендуемый в ppper), после чего алгоритм говорит, что вы должны вычислить величину удвоенного угла в направлениях "x" и "y" (Phi_x и Phi_y).
Phi_x(i,j) = V(i,j) * cos(2*O(i,j))
Phi_y(i,j) = V(i,j) * sin(2*O(i,j))
Magnitude это просто:
V = sqrt(Vx(i,j)^2 + Vy(i,j)^2)
Обратите внимание, что в соответствующей работе не упоминается, что вы должны использовать величину градиента, но это имеет смысл (для меня) в этом. После всех этих исправлений вы можете применить фильтр нижних частот к Phi_x и Phi_y, я использовал простую маску размером 5x5 для усреднения этих величин (что-то вроде medianblur() из opencv).
Последнее, что нужно - это рассчитать новый угол, то есть среднее значение 25-ти соседей в изображении O(i,j), для этого вам просто нужно:
O '(i, j) = 0,5* арктан (Phi_y/Phi_x)
Мы просто здесь... Все это только для вычисления угла НОРМАЛЬНОГО ВЕКТОРА К НАПРАВЛЕНИЯМ Хребта (O'(i,j)) в неперекрывающемся окне BlockSize by BlockSize, что это значит? это означает, что угол, который мы только что вычислили, перпендикулярен гребням, иными словами, мы просто вычислили угол ребер плюс 90 градусов... Чтобы получить нужный нам угол, мы просто должны вычесть полученный угол 90°.
Чтобы нарисовать линии, нам нужно иметь начальную точку (X0, Y0) и конечную точку (X1, Y1). Для этого представьте круг с центром в (X0, Y0) с радиусом "r":
x0 = i + blocksize/2
y0 = j + blocksize/2
r = blocksize/2
Обратите внимание, что мы добавляем i и j к первым координатам, потому что окно движется, и мы будем рисовать линию, начиная с центра неперекрывающегося окна, поэтому мы не можем использовать только центр неперекрывающегося окна. Затем, чтобы вычислить конечные координаты, чтобы нарисовать линию, мы можем просто использовать прямоугольный треугольник так...
X1 = r*cos(O'(i,j)-90°)+X0
Y1 = r*sin(O'(i,j)-90°)+Y0
X2 = X0-r*cos(O'(i,j)-90°)
Y2 = Y0-r*cos(O'(i,j)-90°)
Затем просто используйте функцию линии opencv, где начальная точка (X0, Y0), а конечная точка (X1, Y1). В дополнение к этому я нарисовал окна 16x16 и вычислил точки противоположности X1 и Y1 (X2 и Y2), чтобы нарисовать линию всего окна.
Надеюсь, это поможет кому-нибудь.
Мои результаты...

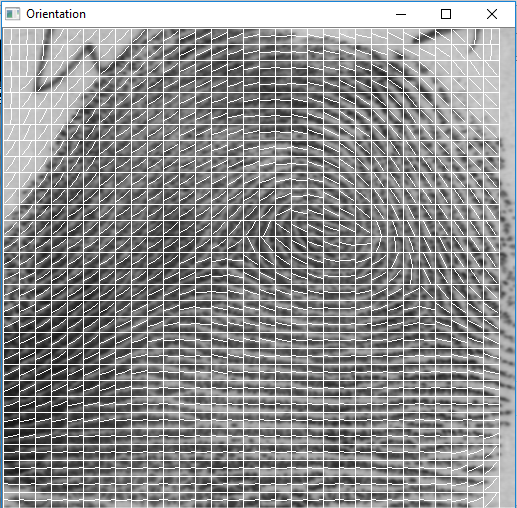
Основная функция:
Mat mat = imread("nwmPa.png",0);
mat.convertTo(mat, CV_32F, 1.0/255, 0);
Normalize(mat);
int blockSize = 6;
int height = mat.rows;
int width = mat.cols;
Mat orientationMap;
orientation(mat, orientationMap, blockSize);
Нормализация:
void Normalize(Mat & image)
{
Scalar mean, dev;
meanStdDev(image, mean, dev);
double M = mean.val[0];
double D = dev.val[0];
for(int i(0) ; i<image.rows ; i++)
{
for(int j(0) ; j<image.cols ; j++)
{
if(image.at<float>(i,j) > M)
image.at<float>(i,j) = 100.0/255 + sqrt( 100.0/255*pow(image.at<float>(i,j)-M,2)/D );
else
image.at<float>(i,j) = 100.0/255 - sqrt( 100.0/255*pow(image.at<float>(i,j)-M,2)/D );
}
}
}
Ориентационная карта:
void orientation(const Mat &inputImage, Mat &orientationMap, int blockSize)
{
Mat fprintWithDirectionsSmoo = inputImage.clone();
Mat tmp(inputImage.size(), inputImage.type());
Mat coherence(inputImage.size(), inputImage.type());
orientationMap = tmp.clone();
//Gradiants x and y
Mat grad_x, grad_y;
// Sobel(inputImage, grad_x, CV_32F, 1, 0, 3, 1, 0, BORDER_DEFAULT);
// Sobel(inputImage, grad_y, CV_32F, 0, 1, 3, 1, 0, BORDER_DEFAULT);
Scharr(inputImage, grad_x, CV_32F, 1, 0, 1, 0);
Scharr(inputImage, grad_y, CV_32F, 0, 1, 1, 0);
//Vector vield
Mat Fx(inputImage.size(), inputImage.type()),
Fy(inputImage.size(), inputImage.type()),
Fx_gauss,
Fy_gauss;
Mat smoothed(inputImage.size(), inputImage.type());
// Local orientation for each block
int width = inputImage.cols;
int height = inputImage.rows;
int blockH;
int blockW;
//select block
for(int i = 0; i < height; i+=blockSize)
{
for(int j = 0; j < width; j+=blockSize)
{
float Gsx = 0.0;
float Gsy = 0.0;
float Gxx = 0.0;
float Gyy = 0.0;
//for check bounds of img
blockH = ((height-i)<blockSize)?(height-i):blockSize;
blockW = ((width-j)<blockSize)?(width-j):blockSize;
//average at block WхW
for ( int u = i ; u < i + blockH; u++)
{
for( int v = j ; v < j + blockW ; v++)
{
Gsx += (grad_x.at<float>(u,v)*grad_x.at<float>(u,v)) - (grad_y.at<float>(u,v)*grad_y.at<float>(u,v));
Gsy += 2*grad_x.at<float>(u,v) * grad_y.at<float>(u,v);
Gxx += grad_x.at<float>(u,v)*grad_x.at<float>(u,v);
Gyy += grad_y.at<float>(u,v)*grad_y.at<float>(u,v);
}
}
float coh = sqrt(pow(Gsx,2) + pow(Gsy,2)) / (Gxx + Gyy);
//smoothed
float fi = 0.5*fastAtan2(Gsy, Gsx)*CV_PI/180;
Fx.at<float>(i,j) = cos(2*fi);
Fy.at<float>(i,j) = sin(2*fi);
//fill blocks
for ( int u = i ; u < i + blockH; u++)
{
for( int v = j ; v < j + blockW ; v++)
{
orientationMap.at<float>(u,v) = fi;
Fx.at<float>(u,v) = Fx.at<float>(i,j);
Fy.at<float>(u,v) = Fy.at<float>(i,j);
coherence.at<float>(u,v) = (coh<0.85)?1:0;
}
}
}
} ///for
GaussConvolveWithStep(Fx, Fx_gauss, 5, blockSize);
GaussConvolveWithStep(Fy, Fy_gauss, 5, blockSize);
for(int m = 0; m < height; m++)
{
for(int n = 0; n < width; n++)
{
smoothed.at<float>(m,n) = 0.5*fastAtan2(Fy_gauss.at<float>(m,n), Fx_gauss.at<float>(m,n))*CV_PI/180;
if((m%blockSize)==0 && (n%blockSize)==0){
int x = n;
int y = m;
int ln = sqrt(2*pow(blockSize,2))/2;
float dx = ln*cos( smoothed.at<float>(m,n) - CV_PI/2);
float dy = ln*sin( smoothed.at<float>(m,n) - CV_PI/2);
arrowedLine(fprintWithDirectionsSmoo, Point(x, y+blockH), Point(x + dx, y + blockW + dy), Scalar::all(255), 1, CV_AA, 0, 0.06*blockSize);
// qDebug () << Fx_gauss.at<float>(m,n) << Fy_gauss.at<float>(m,n) << smoothed.at<float>(m,n);
// imshow("Orientation", fprintWithDirectionsSmoo);
// waitKey(0);
}
}
}///for2
normalize(orientationMap, orientationMap,0,1,NORM_MINMAX);
imshow("Orientation field", orientationMap);
orientationMap = smoothed.clone();
normalize(smoothed, smoothed, 0, 1, NORM_MINMAX);
imshow("Smoothed orientation field", smoothed);
imshow("Coherence", coherence);
imshow("Orientation", fprintWithDirectionsSmoo);
}
кажется ничего не забыл)
Я внимательно прочитал ваш код и обнаружил, что вы ошиблись при вычислении sum3 и sum4:
sum3 += inputImage.at<float>(u,v) * lowPassX.at<float>(i - u*lowPassSize, j - v * lowPassSize);
sum4 += inputImage.at<float>(u, v) * lowPassY.at<float>(i - u*lowPassSize, j - v * lowPassSize);
вместо inputImage следует использовать фильтр нижних частот.