Создание настроенных InputForm и ShortInputForm

Question

Я часто хочу видеть внутреннее представление графических объектов Mathematica не в FullForm но в гораздо более читабельном InputForm возможность выбирать части кода, дважды щелкнув по нему, и легко скопировать этот код в новый вход Cell, Но по умолчанию InputForm не позволяет этого, так как InputForm по умолчанию отображается как Stringне как код Mathematica. Есть ли способ иметь InputForm отображается как код Mathematica?

Я также часто хочу видеть сокращенную версию такого InputForm где все длинные списки координат отображаются в качестве первой координаты, за которой следует количество пропущенных значений координат, заключенных в Skeleton, все пусто Lists удаляются и все номера также сокращаются для отображения не более 6 цифр. Было бы еще лучше использовать 6 цифр только для координат, но для цветовых директив, таких как Hue отображать только 2 значащие цифры. Например,

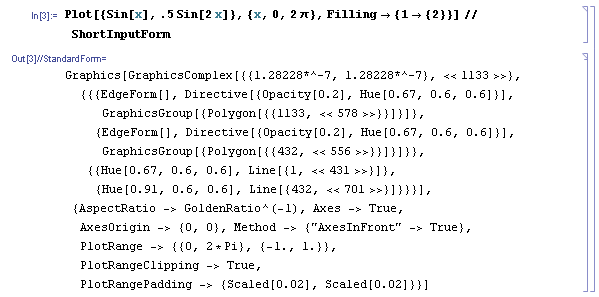
Plot[{Sin[x], .5 Sin[2 x]}, {x, 0, 2 \[Pi]}, 
  Filling -> {1 -> {2}}] // ShortInputForm

должен дать:

Graphics[GraphicsComplex[{{1.28228`*^-7, 1.28228*^-7}, <<1133>>}, 
    {{{EdgeForm[], Directive[{Opacity[0.2], Hue[0.67, 0.6, 0.6]}], 
          GraphicsGroup[{Polygon[{{1133, <<578>>}}]}]}, 
        {EdgeForm[], Directive[{Opacity[0.2], Hue[0.67, 0.6, 0.6]}],              
     GraphicsGroup[{Polygon[{{432, <<556>>}}]}]}}, {{Hue[0.67, 0.6, 
      0.6], Line[{1, <<431>>}]}, {Hue[0.91, 0.6, 0.6], 
          Line[{432, <<701>>}]}}}], {AspectRatio -> GoldenRatio^(-1), 
  Axes -> True, AxesOrigin -> {0, 0}, 
    Method -> {"AxesInFront" -> True}, 
  PlotRange -> {{0, 2*Pi}, {-1., 1}}, 
    PlotRangeClipping -> True, 
  PlotRangePadding -> {Scaled[0.02], Scaled[0.02]}}]

(Обратите внимание, что -0.9999998592131705 преобразуется в -1., 1.2822827157509358*^-7 преобразуется в 1.28228*^-7 а также Hue[0.9060679774997897, 0.6, 0.6] преобразуется в Hue[0.91, 0.6, 0.6]).

Таким образом, я хочу получить вывод InputForm как код Mathematica, а также имеют ShortInputForm функция, которая даст сокращенную версию этого кода. Кто-нибудь может мне помочь?

---

Что касается первой части вопроса, я нашел один способ достичь того, чего я хочу:

Plot[{Sin[x], .5 Sin[2 x]}, {x, 0, 2 \[Pi]}, Filling -> {1 -> {2}}] //
   InputForm // StandardForm

Answer 1

ОБНОВИТЬ

Самая последняя версия shortInputForm Функция может быть найдена здесь.

---

Оригинальный пост

Вот еще одно, даже лучшее решение (совместимо с Mathematica 5):

myInputForm[expr_] := 
 Block[{oldContexts, output, interpretation, skeleton},
  output = ToString[expr, InputForm];
  oldContexts = {$Context, $ContextPath};
  $Context = "myTemp`"; $ContextPath = {$Context};
  output = DisplayForm@ToBoxes[ToExpression[output] /.
      {myTemp`interpretation -> If[$VersionNumber >= 6,
         System`Interpretation, System`First@{#} &],
       myTemp`Row -> System`Row,
       myTemp`skeleton -> System`Skeleton,
       myTemp`sequence :> (System`Sequence @@ # &)}, StandardForm];
  {$Context, $ContextPath} = oldContexts; output]
shortInputForm[expr_] := myInputForm[expr /. {{} -> Sequence[],
    lst : {x_ /; VectorQ[x, NumberQ], y__} /;
      (MatrixQ[lst, NumberQ] && Length[lst] > 3) :>
     {x /. v : {a_, b__} /; Length[v] > 3 :>
        {a, interpretation[skeleton[Length[{b}]], sequence@{b}]},
      interpretation[skeleton[Length[{y}]], sequence@{y}]},
    lst : {x_, y__} /; VectorQ[lst, NumberQ] && Length[lst] > 3 :>
     {x, interpretation[skeleton[Length[{y}]], sequence@{y}]}}]

Как это устроено

Это решение основано на простой идее: нам нужно заблокировать преобразование таких вещей, как Graphics, Point и другие, чтобы набирать выражения для отображения их во внутренней форме (как выражения, подходящие для ввода). К счастью, если мы сделаем это, в результате StandardForm Выходные данные считаются только отформатированными (двумерными) InputForm оригинального выражения. Это как раз то, что нужно!

Но как это сделать? Прежде всего, это преобразование сделаноFormatValues определено для Symbolкак Graphics, Point и т.д. Можно получить полный список таких Symbols путем оценки следующего:

list = Symbol /@ 
  Select[DeleteCases[Names["*"], "I" | "Infinity"], 
   ToExpression[#, InputForm, 
     Function[symbol, Length[FormatValues@symbol] > 0, HoldAll]] &]

Моя первая идея была просто Block все эти Symbols (и это работает!):

myInputForm[expr_] := 
 With[{list = list}, Block[list, RawBoxes@MakeBoxes@expr]]

Но этот метод приводит к оценке всех этих Symbolс, а также оценивает все FormatValues для всех Symbolв $ContextPath, Я думаю, этого следует избегать.

Другой способ заблокировать эти FormatValues это просто удалить контекст "System`" от $ContextPath, Но это работает только если эти Symbolс еще не разрешены "System`" контекст. Поэтому нам нужно сначала преобразовать наше выражение в Stringзатем удалите "System`" контекст из $ContextPath и, наконец, преобразовать строку назад в исходное выражение. Тогда все новое Symbols будет связан с текущим $Context (а также Graphics, Point и т.д. - тоже, поскольку их нет в $ContextPath). Для предотвращения конфликтов контекста и засорения "Global`" контекст я переключаю $Context в "myTemp`" которые могут быть легко очищены при необходимости.

Вот как myInputForm работает.

Теперь о shortInputForm, Идея состоит не только в том, чтобы отобразить сокращенную версию myInputForm но также сохраните возможность выбирать и копировать части сокращенного кода в новую входную ячейку и использовать этот код, поскольку это был бы полный код без сокращений. В версии 6 и выше можно добиться последнего с Interpretation, Для совместимости с пре-6 версиями Mathematica Я добавил кусок кода, который удаляет эту способность, если $VersionNumber меньше 6.

Единственная проблема, с которой я столкнулся при работе с Interpretation что у него нет SequenceHold атрибут и поэтому мы не можем просто указать Sequence в качестве второго аргумента для Interpretation, Но этой проблемы можно легко избежать, обернув последовательность в List а потом ApplyИНГ Sequence к нему:

System`Sequence @@ # &

Обратите внимание, что мне нужно указать точный контекст для всех встроенных SymbolЯ использую, потому что в момент их вызова "System`" контекст не в $ContextPath,

На этом заканчиваются нестандартные решения, принятые мной при разработке этих функций. Предложения и комментарии приветствуются!

Answer 2

На данный момент я пришел к следующему решению:

round[x_, n_] := (10^-n*Round[10^n*MantissaExponent[x]]) /.
   {m_, e_} :> N[m*10^e];
ShortInputForm[expr_] := ((expr /.
       {{} -> Sequence[],
        lst : {x_ /; VectorQ[x, NumberQ], y__} /;
          (MatrixQ[lst, NumberQ] && Length[lst] > 2) :>
         {x, Skeleton[Length[{y}]]},
        lst : {x_, y__} /; VectorQ[lst, NumberQ] && Length[lst] > 2 :>
         {x, Skeleton[Length[{y}]]}} /.
      {exp : Except[List | Point][x__] /; 
         VectorQ[{x}, MachineNumberQ] :>
        (round[#, 2] & /@ exp), 
       x_Real /; MachineNumberQ[x] :> round[x, 6]})
    // InputForm // StandardForm)

Сейчас: