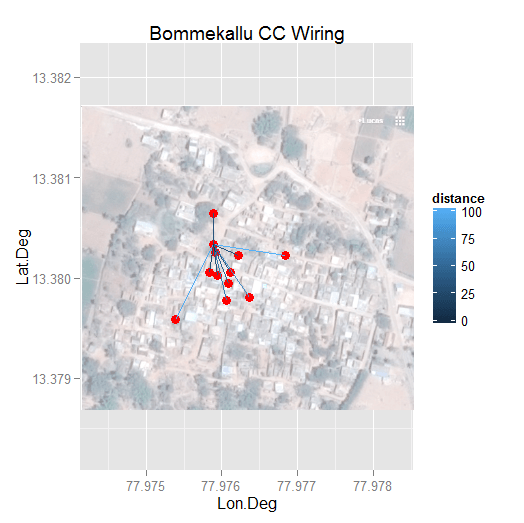
Наименьшая длина провода подключения к сети

Question

Я строю микросеть, поэтому мне нужно подключить около 12 домов к центральному источнику солнечной энергии. Проводка здесь является основной ценой, поэтому я пытаюсь придумать конфигурацию, которая минимизирует длину провода. Это похоже, но не совсем как проблема коммивояжера, потому что несколько проводов могут выходить из одного источника - если бы это был один провод / путь, это было бы точно так же, как TSP.

Итак, мой вопрос:

Кто-нибудь знает алгоритм определения кратчайшего способа соединения всех точек, где есть центральная точка, которая может соединять неопределенное количество окружающих точек? Окончательное решение должно напоминать график, в котором n-1 узлы имеют максимум два ребра, соединяющих их, а один может иметь до n-1 ребер? В частности, есть ли способ сделать это в R?

РЕДАКТИРОВАТЬ, ЧТОБЫ ПОКАЗАТЬ КОД / УСИЛИЕ

Я решил это относительно простым способом, предполагая единственный путь. И я решил, предполагая, что каждый дом подключен напрямую к источнику питания. Вот этот код:

############ interested users Wire CalculationBommekalla Analysis
require(png)
require(grid)
require(arm)
require(DCluster)
require(ggplot2)

setwd("C:/Users/Lucas/Documents/India2014_2015/ADATS Docs/BoomekallaAnalysis")

data= read.csv("BommekallInterestedUsers.csv")
summary(data)
names(data)

data$ind = c(1:nrow(data))

##### Analysis

# Shortest Path

distFrame = data[,c("Lon.Deg", "Lat.Deg")]
dists= as.matrix(dist(distFrame, upper=TRUE))
diag(dists)=1000


current= which(data.WO$ind==11)  # sushilemma
ord = rep(current,length=nrow(data.WO))
dists[,current]=1000

for (j in c(1:(nrow(data.WO)-1))){
    current= which(dists[current,]==min(dists[current,]))
    dists[,current]=1000
    ord[j+1] = current
}

# line calculation
firstHouses= data.WO[ord,]
secondHouses= data.WO[c(ord[-1],NA),]

lines = data.frame(lonA = firstHouses$Lon.Deg, 
    latA= firstHouses$Lat.Deg, 
    lonB = secondHouses$Lon.Deg,
    latB = secondHouses$Lat.Deg)
lines= na.omit(lines)

# Spider web -- completely connected to source

ccLines = data.frame(latA = data$Lat.Deg[
    data$Name=="Sushilemma"], latB = data$Lat.Deg,
    lonA = data$Lon.Deg[data$Name=="Sushilemma"],
    lonB = data$Lon.Deg) 

# Haversine Distance -- atanh_trans() is arctan

linesRads=lines*pi/180

a= with(linesRads, sin((latB-latA)/2)^2+
    cos(latB)*cos(latA)*sin((lonB-lonA)/2)^2)
c= 2*asin(pmin(1,sqrt(a)))
lines$distance=6371*c*1000

totalDistance = sum(lines$distance)

totalCost = totalDistance*15