Как создать трехмерную карту пространственной плотности?
У меня есть зависящая от времени система различного количества частиц (~100k частиц). Фактически, каждая частица представляет собой взаимодействие в трехмерном пространстве с определенной силой. Таким образом, каждая частица имеет (X,Y,Z;w), которая является координатой плюс весовой коэффициент между 0 и 1, показывая силу взаимодействия в этой координате. Здесь http://pho.to/9Ztti Я загрузил 10 снимков системы в реальном времени, причем частицы представлены в виде красноватых маленьких точек; чем краснее точка, тем сильнее взаимодействие.
Вопрос в том, как создать трехмерную (пространственную) карту плотности этих частиц, предпочтительно в Matlab или Origin Pro 9 или ImageJ? Можно ли, скажем, взять среднее значение этих изображений на основе интенсивности красного цвета в ImageJ?
Поскольку у меня есть числовые данные для частиц (X,Y,Z;w), я могу анализировать эти данные и в других программах. Итак, вы можете предложить любой другой аналитический подход / программное обеспечение
Любые идеи / комментарии приветствуются!
3 ответа
Предполагая, что ваши данные находятся в трехмерном непрерывном пространстве, а ваш набор данных - это просто список трехмерных положений взаимодействия каждой частицы, звучит так, как будто вы хотите создать 4D взвешенную гистограмму. Вам нужно будет нарезать трехмерное пространство на ячейки и суммировать взвешенные точки в каждой ячейке с течением времени, а затем отобразить результаты на одном трехмерном графике, где цвет представляет суммированные взвешенные взаимодействия с течением времени.
Вот пример со случайно сгенерированными взаимодействиями частиц:
%% Create dataSet of random particle interations in 3d space
for i=1:5000
if i == 1
dataSet = [rand()*100 rand()*100 rand()*100 rand() i];
else
dataSet(i,:) = [rand()*100 rand()*100 rand()*100 rand() i];
end
end
% dataSet = [x y z interactionStrength imageNumber]
xLimits = [min(dataSet(:,1)) max(dataSet(:,1))];
yLimits = [min(dataSet(:,2)) max(dataSet(:,2))];
zLimits = [min(dataSet(:,3)) max(dataSet(:,3))];
binSize = 10; % Number of bins to split each spatial dimention into
binXInterval = (xLimits(2)-xLimits(1))/binSize;
binYInterval = (yLimits(2)-yLimits(1))/binSize;
binZInterval = (zLimits(2)-zLimits(1))/binSize;
histo = [];
for i=xLimits(1)+(binSize/2):binXInterval:xLimits(2) + (binSize/2)
for j=yLimits(1)+(binSize/2):binYInterval:yLimits(2) + (binSize/2)
for k=zLimits(1)+(binSize/2):binZInterval:zLimits(2) + (binSize/2)
%% Filter out particle interactions found within the current spatial bin
idx = find((dataSet(:,1) > (i - binSize)) .* (dataSet(:,1) < i));
temp = dataSet(idx,:);
idx = find((temp(:,2) > (j - binSize)) .* (temp(:,2) < j));
temp = temp(idx,:);
idx = find((temp(:,3) > (k - binSize)) .* (temp(:,3) < k));
temp = temp(idx,:);
%% Add up all interaction strengths found within this bin
histo = [histo; i j k sum(temp(:,4))];
end
end
end
%% Remove bins with no particle interactions
idx = find(histo(:,4)>0);
histo = histo(idx,:);
numberOfImages = max(dataSet(:,5));
%% Plot result
PointSizeMultiplier = 100000;
scatter3(histo(:,1).*binXInterval + xLimits(1),histo(:,2).*binYInterval + yLimits(1),histo(:,3).*binZInterval + zLimits(1),(histo(:,4)/numberOfImages)*PointSizeMultiplier,(histo(:,4)/numberOfImages));
colormap hot;
%Size and color represent the average interaction intensity over time
4-мерная гистограмма из 10000 случайно сгенерированных взаимодействий частиц. Каждая ось разделена на 10 бункеров. Размер и цвет представляют суммированные взаимодействия частиц в каждом бине с течением времени: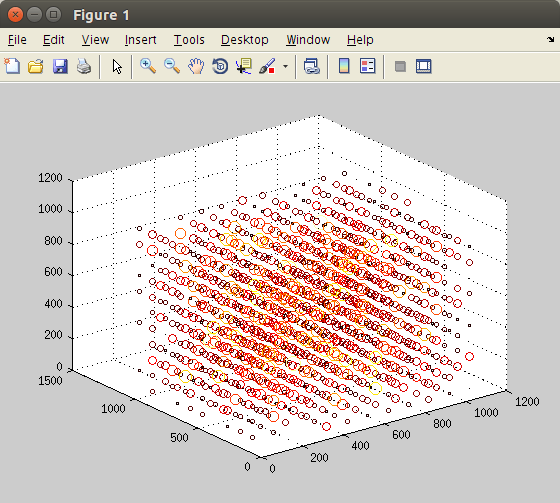
Если ваша система может обрабатывать матрицу в Matlab, это может быть так же просто, как
A = mean(M, 4);
Если предположить, M содержит 4D компиляцию ваших изображений, то A будет вашей картой.
Одним из способов будет использование трехмерного графика рассеяния (пузырьков) с переменными размерами окружности / пузырей, пропорциональными интенсивности вашей частицы.
Вот смоделированный пример:
N = 1e4; % number of particles
X = randn(N,1); % randomly generated coordinates
Y = 2*randn(N,1);
Z = 0.5*randn(N,1);
S = exp(-sqrt(X.^2 + Y.^2 + Z.^2)); % bubble size vector
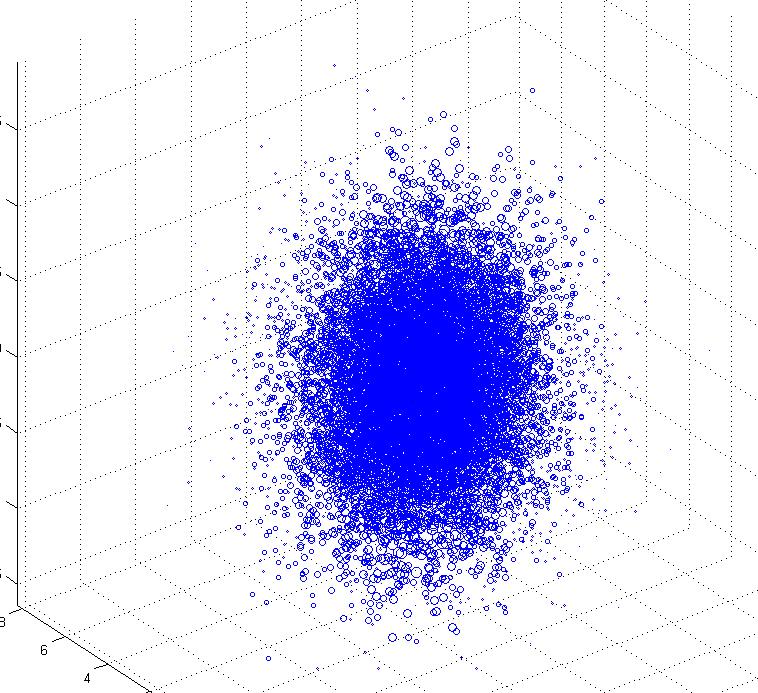
scatter3(X,Y,Z,S*200)
 конец
конец
Здесь я случайно сгенерировал значения для X, Y и Z, а S обратно пропорционально расстоянию от центра облака.
В вашем случае, если мы предположим, что значения (X,Y,Z,w) хранятся в двумерном массиве под названием Частицы, это будет:
X = Particles(:,1);
Y = Particles(:,2);
Z = Particles(:,3);
S = Particles(:,4);
Надеюсь, что это помогло.