Неточность БПФ для C#

Question

Я экспериментировал с алгоритмом FFT. Я использую NAudio вместе с рабочим кодом алгоритма FFT из Интернета. Исходя из моих наблюдений за исполнением, результирующий шаг является неточным.

Что происходит, так это то, что у меня есть MIDI (сгенерированный из GuitarPro), конвертированный в WAV-файл (44,1 кГц, 16-битный, моно), который содержит прогрессию высоты тона, начиная с E2 (самая низкая гитарная нота) до примерно E6. Какие результаты для нижних нот (около E2-B3), как правило, очень неправильно. Но достижение C4 несколько корректно в том смысле, что вы уже можете видеть правильную прогрессию (следующая нота - C#4, затем D4 и т. Д.). Однако проблема заключается в том, что обнаруженная высота звука на полшага ниже, чем фактическая высота звука (например, C4 должен быть примечанием, но отображается D#4).

Что вы думаете может быть не так? Я могу опубликовать код, если это необходимо. Спасибо большое! Я все еще начинаю понимать область DSP.

Редактировать: Вот грубая царапина того, что я делаю

byte[] buffer = new byte[8192];
int bytesRead;
do
{
  bytesRead = stream16.Read(buffer, 0, buffer.Length);
} while (bytesRead != 0);

И затем: (waveBuffer - это просто класс, который должен конвертировать byte[] в float[], так как функция принимает только float[])

public int Read(byte[] buffer, int offset, int bytesRead)
{
  int frames = bytesRead / sizeof(float);
  float pitch = DetectPitch(waveBuffer.FloatBuffer, frames);
}

И наконец: (Smbpitchfft - это класс, у которого есть алгоритм FFT... я считаю, что в этом нет ничего плохого, поэтому я не публикую его здесь)

private float DetectPitch(float[] buffer, int inFrames)
{
  Func<int, int, float> window = HammingWindow;
  if (prevBuffer == null)
  {
    prevBuffer = new float[inFrames]; //only contains zeroes
  }  

  // double frames since we are combining present and previous buffers
  int frames = inFrames * 2;
  if (fftBuffer == null)
  {
    fftBuffer = new float[frames * 2]; // times 2 because it is complex input
  }

  for (int n = 0; n < frames; n++)
  {
     if (n < inFrames)
     {
       fftBuffer[n * 2] = prevBuffer[n] * window(n, frames);
       fftBuffer[n * 2 + 1] = 0; // need to clear out as fft modifies buffer
     }
     else
     {
       fftBuffer[n * 2] = buffer[n - inFrames] * window(n, frames);
       fftBuffer[n * 2 + 1] = 0; // need to clear out as fft modifies buffer
     }
   }
   SmbPitchShift.smbFft(fftBuffer, frames, -1);
  }

И для интерпретации результата:

float binSize = sampleRate / frames;
int minBin = (int)(82.407 / binSize); //lowest E string on the guitar
int maxBin = (int)(1244.508 / binSize); //highest E string on the guitar

float maxIntensity = 0f;
int maxBinIndex = 0;

for (int bin = minBin; bin <= maxBin; bin++)
{
    float real = fftBuffer[bin * 2];
    float imaginary = fftBuffer[bin * 2 + 1];
    float intensity = real * real + imaginary * imaginary;
    if (intensity > maxIntensity)
    {
        maxIntensity = intensity;
        maxBinIndex = bin;
    }
}

return binSize * maxBinIndex;

ОБНОВЛЕНИЕ (если кто-то еще заинтересован):

Итак, в одном из ответов ниже указано, что пик частоты от БПФ не всегда эквивалентен высоте тона. Я это понимаю. Но я хотел попробовать что-то для себя, если бы это было так (при условии, что бывают периоды, когда пик частоты является результирующим шагом). В общем, я получил 2 программного обеспечения (SpectraPLUS и FFTProperties от DewResearch; кредиты для них), которые способны отображать частотную область для аудиосигналов.

Итак, вот результаты частотных пиков во временной области:

SpectraPLUS

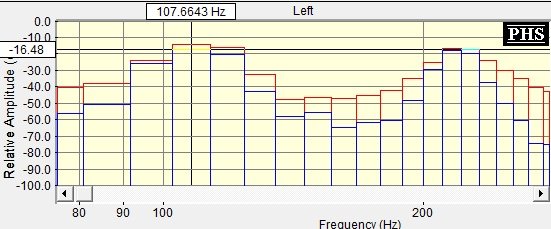
и БПФ свойства:

Это было сделано с использованием тестовой ноты A2 (около 110 Гц). Посмотрев на изображения, они имеют пики частоты в диапазоне 102-112 Гц для SpectraPLUS и 108 Гц для свойств FFT. В моем коде я получаю 104 Гц (я использую 8192 блока и частоту дискретизации 44,1 кГц... 8192 затем удваивается, чтобы сделать его сложным входным сигналом, поэтому в итоге я получаю около 5 Гц для двоичного размера по сравнению с 10 Гц для SpectraPLUS).

Так что теперь я немного запутался, так как в программном обеспечении они, кажется, возвращают правильный результат, но в моем коде я всегда получаю 104 Гц (обратите внимание, что я сравнил функцию FFT, которую я использовал с другими, такими как Math.Net, и кажется, что будь прав).

Вы думаете, что проблема может быть с моей интерпретацией данных? Или программное обеспечение делает что-то еще до отображения частотного спектра? Спасибо!

Answer 1

Похоже, у вас могут быть проблемы с интерпретацией с выходом FFT. Несколько случайных точек:

• БПФ имеет конечное разрешение - каждый выходной лоток имеет разрешение Fs / N, где Fs частота дискретизации и N это размер БПФ

• для нот с низкой музыкальной шкалой разница в частоте между последовательными нотами относительно невелика, поэтому вам потребуется достаточно большой N, чтобы различать ноты, которые находятся на полутоне (см. примечание 1 ниже)

• первый контейнер (индекс 0) содержит энергию с центром в 0 Гц, но включает энергию от +/- Fs / 2N

• бункер i содержит энергию с центром в i * Fs / N но включает в себя энергию от +/- Fs / 2N любая сторона этой центральной частоты

• Вы получите спектральную утечку из смежных бинов - насколько это плохо, зависит от того, какую оконную функцию вы используете - без окна (== прямоугольное окно), а спектральная утечка будет очень плохой (очень широкие пики) - для оценки частоты вы хотите выбрать оконная функция, которая дает вам острые пики

• высота звука - это не то же самое, что частота - высота - это восприятие, частота - это физическая величина - воспринимаемая высота звука музыкального инструмента может немного отличаться от основной частоты, в зависимости от типа инструмента (некоторые инструменты даже не производят значительных энергия на их основной частоте, но мы все еще воспринимаем их высоту, как если бы присутствовали основные)

Однако я думаю, что из доступной ограниченной информации вы, возможно, "где-то один" где-то в преобразовании индекса бина в частоту, или, возможно, ваше БПФ слишком мало, чтобы дать вам достаточное разрешение для низких нот, и вам может понадобиться увеличить Н.

Вы также можете улучшить оценку основного тона с помощью нескольких методов, таких как кепстральный анализ, или с помощью анализа фазового компонента выходного сигнала БПФ и сравнения его для последовательных БПФ (это позволяет получить более точную оценку частоты в пределах ячейки для данного размера БПФ).).

---

Заметки

(1) Просто, чтобы обозначить это цифрой, E2 составляет 82,4 Гц, F2 - 87,3 Гц, поэтому вам нужно разрешение несколько лучше, чем 5 Гц, чтобы различать две самые низкие ноты на гитаре (и намного лучше, чем это, если вы на самом деле хочу сделать, скажем, точный тюнинг). При выборке 44,1 кГц вам, вероятно, понадобится БПФ, по крайней мере, N = 8192, чтобы получить достаточное разрешение (44100 / 8192 = 5,4 Гц), вероятно, N = 16384 будет лучше.

Answer 2

Я думал, что это может помочь вам. Я сделал несколько сюжетов из 6 открытых струн гитары. Код написан на Python с использованием pylab, который я рекомендую для экспериментов:

# analyze distorted guitar notes from
# http://www.freesound.org/packsViewSingle.php?id=643
#
# 329.6 E - open 1st string
# 246.9 B - open 2nd string
# 196.0 G - open 3rd string
# 146.8 D - open 4th string
# 110.0 A - open 5th string
#  82.4 E - open 6th string

from pylab import *
import wave

fs = 44100.0 
N = 8192 * 10
t = r_[:N] / fs
f = r_[:N/2+1] * fs / N 
gtr_fun = [329.6, 246.9, 196.0, 146.8, 110.0, 82.4]

gtr_wav = [wave.open('dist_gtr_{0}.wav'.format(n),'r') for n in r_[1:7]]
gtr = [fromstring(g.readframes(N), dtype='int16') for g in gtr_wav]
gtr_t = [g / float64(max(abs(g))) for g in gtr]
gtr_f = [2 * abs(rfft(g)) / N for g in gtr_t]

def make_plots():
    for n in r_[:len(gtr_t)]:
        fig = figure()
        fig.subplots_adjust(wspace=0.5, hspace=0.5)
        subplot2grid((2,2), (0,0))
        plot(t, gtr_t[n]); axis('tight')
        title('String ' + str(n+1) + ' Waveform')
        subplot2grid((2,2), (0,1))
        plot(f, gtr_f[n]); axis('tight')
        title('String ' + str(n+1) + ' DFT')
        subplot2grid((2,2), (1,0), colspan=2)
        M = int(gtr_fun[n] * 16.5 / fs * N)
        plot(f[:M], gtr_f[n][:M]); axis('tight')
        title('String ' + str(n+1) + ' DFT (16 Harmonics)')

if __name__ == '__main__':
    make_plots()
    show()

Строка 1, основной = 329,6 Гц:

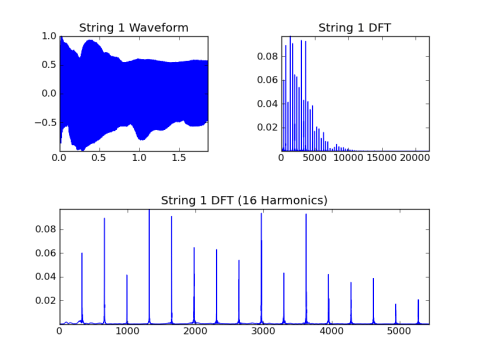
Строка 2, основной = 246,9 Гц:

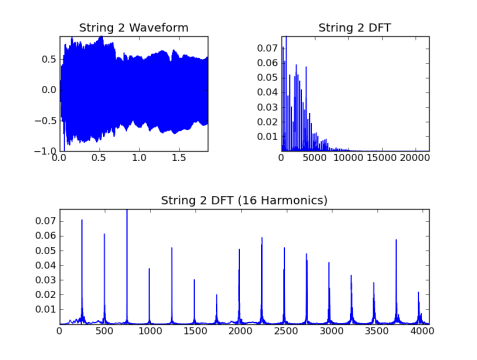
Строка 3, основной = 196,0 Гц:

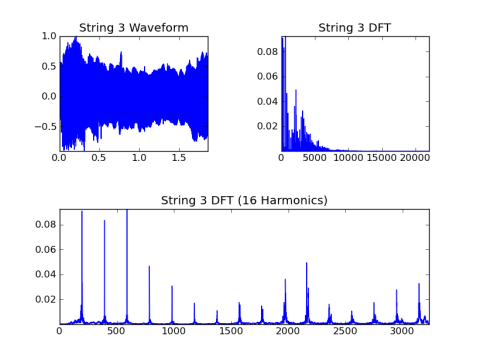
Строка 4, основной = 146,8 Гц:

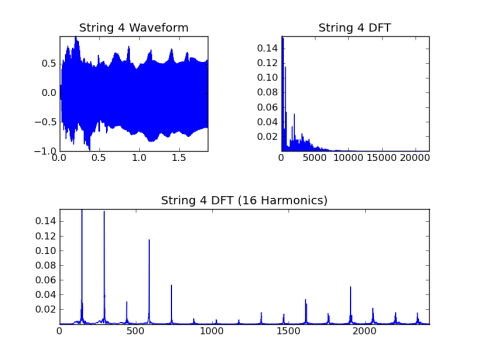
Строка 5, основной = 110,0 Гц:

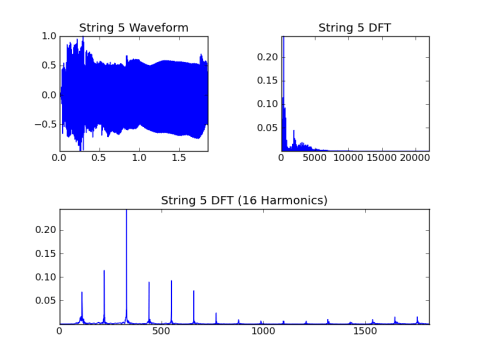
Строка 6, основная = 82,4 Гц:

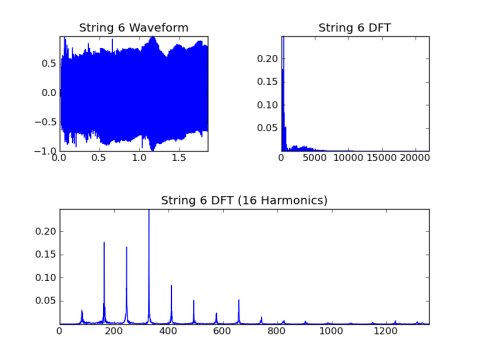
Основная частота не всегда является доминирующей гармоникой. Он определяет расстояние между гармониками периодического сигнала.

Answer 3

У меня был похожий вопрос, и ответом для меня было использование Goertzel вместо FFT. Если вы знаете, какие тоны вы ищете (MIDI), Гертцель способен обнаруживать тоны с точностью до одной синусоидальной волны (один цикл). Он делает это, генерируя синусоидальную волну звука и "помещая ее поверх необработанных данных", чтобы увидеть, существует ли она. БПФ производит выборку больших объемов данных для получения приблизительного частотного спектра.

Answer 4

Музыкальный слух отличается от частоты пика. Pitch - это психо-перцептивное явление, которое может зависеть больше от обертонов и тому подобного. Частота того, что человек назвал бы высотой тона, могла бы отсутствовать или быть совсем небольшой в реальных спектрах сигналов.

И частотный пик в спектре может отличаться от любого бин-центра БПФ. Центральные частоты бункера БПФ будут меняться по частоте и интервалу в зависимости только от длины БПФ и частоты дискретизации, а не от спектров в данных.

Таким образом, у вас есть как минимум 2 проблемы, с которыми нужно бороться. Есть тонна научных работ по оценке частоты, а также отдельная тема оценки основного тона. Начни там.