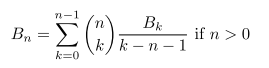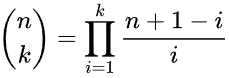Функция Бернулли в Haskell

Question

Я хочу написать функцию Бернулли bernoulli:: Integer -> Rationalв haskell, используя следующий алгоритм вычисления числа Бернулли для заданного целого числа.

функции «frac» и «binom» используются для вычисления бинома в определении. это то, что у меня есть до сих пор:

      fact :: Integer -> Integer
fact i = foldr (*) 1 [1..i]

binom :: Integer -> Integer -> Integer
binom n k = (fact n) `div` (fact k* fact (n-k))

bernoulli :: Integer -> Rational
bernoulli 0 = 1
bernoulli i = ((binom i j) * (bernoulli j)) / (j - i - 1) where j = i-1

Я пробовал это несколько раз, но либо рекурсия не работает, либо результирующий Rational неверен.

Answer 1

Я нашел три проблемы в вашем коде:

1. скобки в binom
2. Смешивание Rationalа также Integer
3. Ваша функция не сумма, а только первый член

В моем коде вы можете увидеть, как я справился с этими проблемами.

      fact :: Integer -> Integer
fact i = foldr (*) 1 [1..i]

binom :: Integer -> Integer -> Integer
binom n k = (fact n) `div` ((fact k) * fact (n-k))

bernoulli :: Integer -> Rational
bernoulli 0 = 1
bernoulli n = sum [
    toRational(binom n k) * (bernoulli k) / toRational(k - n - 1)
    | k <- [0..(n-1)]
  ]

Тест:

      map bernoulli [0..10]

Выход:

      [1 % 1,(-1) % 2,1 % 6,0 % 1,(-1) % 30,0 % 1,1 % 42,0 % 1,(-1) % 30,0 % 1,5 % 66]

Небольшое дополнение:
если мы не будем следовать правилу использования существующих библиотек, решение также может выглядеть так:

      binom :: Rational -> Rational -> Rational
binom n k = product [ ( n + 1 - i ) / i | i <- [ 1 .. k ] ]

bernoulli :: Rational -> Rational
bernoulli 0 = 1
bernoulli n = sum [
    binom n k * bernoulli k / (k - n - 1)
    | k <- [0..(n-1)]
  ]

Потому что:

Обратите внимание на сходство программы с математической записью.

PS bernoulliс foldr:

      bernoulli :: Integer -> Rational
bernoulli n = foldr (summand n) (0::Rational) [0 .. (n-1)]
  where
    summand n k s1 = s1 + toRational(binom n k) * bernoulli k / toRational(k - n - 1)