Найти решение для повторения: T(N) = 2 T(N/4 + √N) + (√10) N

Question

При решении сложного уравнения повторения, как это T(N) = 2 T(N/4 + √N) + (√10) N ;T(1) = 1

Я попытался внести некоторые изменения в переменные, чтобы упростить их и решить с помощью основной теоремы, но мне это не удалось, поэтому я выбрал доминирующую, поэтому она будет такой:T(N) = 2 T(N/4) + (√10) N так что, это T(N)=Θ(N), Это правда или нет?

Answer 1

Попытки развернуть рекурсию или сделать замену не оставили меня никуда. Так что единственное, что мне удалось сделать, это увидеть, что 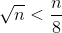для любого достаточно большого n (выше 64). Вы можете выбрать любое число (не только 8), больше 4.

Таким образом, вы в конечном итоге

Решая это с помощью теоремы мастера, вы видите, что она падает в первом случае с ,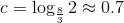

Поэтому решение Θ(N) что так же, как вы задавались вопросом.