Как самобалансирующееся дерево или структура дерева небольшой высоты помогает создавать эффективные списки и абстрактную структуру данных

Question

Я читаю о дереве AVL, и там я перенаправил на само балансирующее дерево, там я прочитал, что

В информатике самообалансированное (или сбалансированное по высоте) дерево двоичного поиска - это любое дерево двоичного поиска на основе узлов, которое автоматически сохраняет свою высоту (максимальное количество уровней ниже корня) малой по отношению к произвольным вставкам и удалениям элементов. 1

Эти структуры обеспечивают эффективные реализации для изменяемых упорядоченных списков и могут использоваться для других абстрактных структур данных, таких как ассоциативные массивы, очереди с приоритетами и наборы.

Я не совсем понимаю

1. Каково отношение высоты к списку? массив?
2. Как дерево малой высоты обеспечивает эффективную реализацию изменяемых упорядоченных списков? массив? Очереди?
3. Предположим, что узел списка или индекса массива является высотой списка или массива, насколько он может быть маленьким?

Answer 1

Вот визуальный баланс 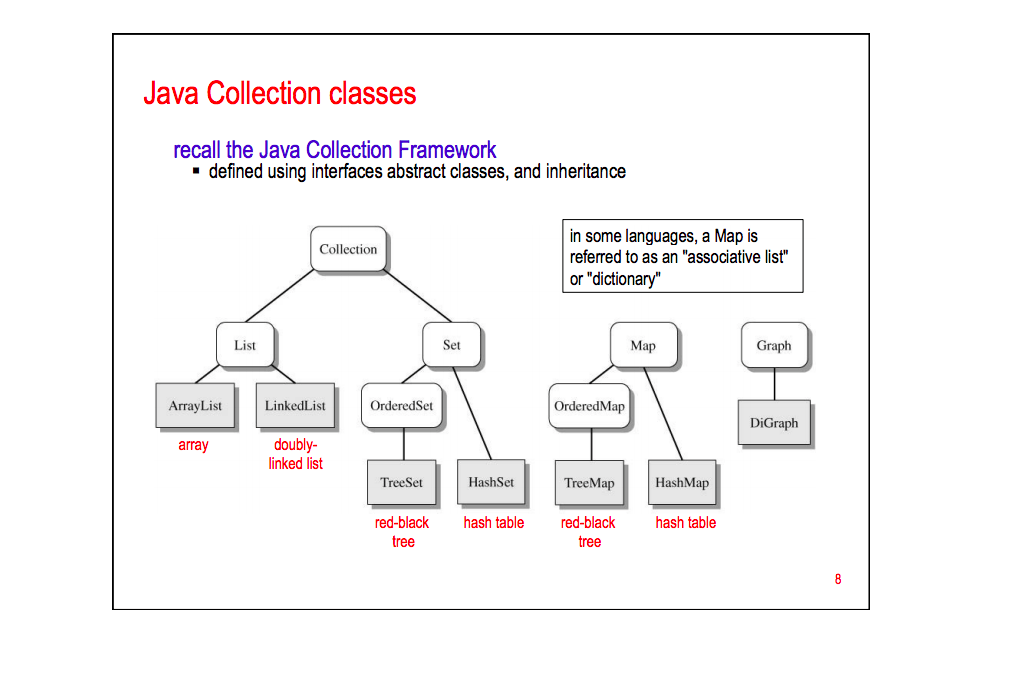2. Помните, что деревья предлагают уникальный путь к каждому узлу. Поскольку деревья AVL являются бинарными деревьями поиска, мы "знаем", в каком направлении идти, если дано значение, потому что дерево отсортировано. Деревья AVL (для каждого узла высоты левого и правого поддеревьев различаются не более чем на 1) позволяют осуществлять быстрый поиск и вставку, обычно записывают N, поскольку он может вращаться и манипулировать собой в постоянное время. Мы можем внедрить упорядоченные значения списка, очереди и т. Д. В древовидную структуру, чтобы использовать ее характеристики. Ключ остается сбалансированным деревом (остается горизонтальным, а не вертикальным, что он делает, следуя признаку бинарного дерева поиска).

Можете ли вы уточнить на 1 и 3?