Используя аппаратный рнг из питона

Question

Существуют ли какие-либо готовые библиотеки, чтобы аппаратное обеспечение prng (rdrand) от Intel могло использоваться программами-пустышками для заполнения буферов случайных чисел?

В противном случае кто-то может указать мне правильное направление для некоторого кода на C, который я мог бы адаптировать или использовать (я использую CPython и Cython с numpy, так что достаточно минимальной обертки).

Генераторы случайных чисел, которые я хочу, являются равномерными случайными числами между [0,1).

Answer 1

Этот код будет использовать API / dev / urandom (Unix) или CryptGenRandom (Windows). Какой RNG используется, аппаратный или программный, зависит от операционной системы.

Если вы хотите точно определить, какой генератор используется, вы должны запросить его через его аппаратный драйвер или библиотеку. Когда у вас есть случайные биты в виде строки, вы поступаете аналогично этому коду, используя np.fromstring.

Обычно мы можем доверять операционной системе использовать лучшие источники энтропии для своих криптографических служб, включая генератор случайных битов. Если имеется аппаратный ГСЧ, его можно использовать, как правило, в сочетании с другими источниками энтропии.

import os
import numpy as np

def cryptorand(n):
    a = np.fromstring(os.urandom(n*4), dtype=np.uint32) >> 5
    b = np.fromstring(os.urandom(n*4), dtype=np.uint32) >> 6
    return (a * 67108864.0 + b) / 9007199254740992.0

Вот распределение 1 000 000 случайных отклонений, сгенерированных этим методом в Mac OS X. Как вы можете видеть, оно довольно равномерно для [0,1):

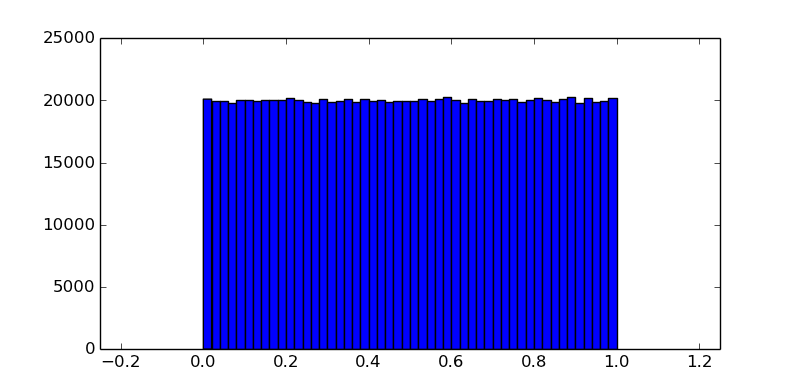
Если вам нужны действительно сильные криптографические случайные отклонения, вы можете использовать /dev/random вместо /dev/urandom. Это относится только к Unix-подобным системам, а не к Windows:

import numpy as np

def cryptorand(n):
    with open('/dev/random','rb') as rnd:
        a = np.fromstring(rnd.read(n*4), dtype=np.uint32) >> 5
        b = np.fromstring(rnd.read(n*4), dtype=np.uint32) >> 6
        return (a * 67108864.0 + b) / 9007199254740992.0

Обратите внимание, что эта функция может блокироваться, в отличие от версии, которая использует os.urandom в качестве источника энтропии.

(Edit1: обновлена ​​нормализация, чтобы приравнять ее к NumPy)

Изменить 2: комментарии указывают, что причиной вопроса была скорость, а не криптографическая сила. Цель аппаратного RNG - не скорость, а сила, поэтому он делает вопрос недействительным. Тем не менее, быстрый и хороший PRNG, который может стать альтернативой Mersenne Twister, - это генератор Джорджа Марсаглии с множеством переносов. Вот простая реализация в Cython:

import numpy as np
cimport numpy as cnp

cdef cnp.uint32_t gw = 152315241 # any number except 0 or 0x464fffff
cdef cnp.uint32_t gz = 273283728 # any number except 0 or 0x9068ffff

def rand(cnp.intp_t n):
    """Generate n random numbers using George Marsaglia's 
    multiply-with-carry method."""
    global gw, gz
    cdef cnp.uint32_t w, z, a, b
    cdef cnp.intp_t i
    cdef cnp.ndarray x = cnp.PyArray_SimpleNew(1, &n, cnp.NPY_FLOAT64)
    cdef cnp.float64_t *r = <cnp.float64_t*> cnp.PyArray_DATA(x)
    w,z = gw,gz
    for i in range(n): 
        z = 36969 * (z & 65535) + (z >> 16)
        w = 18000 * (w & 65535) + (w >> 16)
        a = (z << 16) + w
        z = 36969 * (z & 65535) + (z >> 16)
        w = 18000 * (w & 65535) + (w >> 16)
        b = (z << 16) + w
        r[i] = (a * 67108864.0 + b) / 9007199254740992.0
    gw,gz = w,z
    return x

Остерегайтесь, что ни Mersenne Twister, ни умножение с переносом не имеют криптографической силы.

Answer 2

Да. Есть модуль rdrand.

Answer 3

Доступна статья здесь ( http://iopscience.iop.org/article/10.3847/1538-4357/aa7ede/meta;jsessionid=A9DA9DDB925E6522D058F3CEEC7D0B21.ip-10-40-2-120) и (не платная версия) здесь ( https://arxiv.org/abs/1707.02212), где описано, как использовать Intel Secure Key, который представляет собой криптографически безопасный генератор случайных чисел, реализованный на кристалле. Доступ к нему можно получить через инструкции RdRand и RdSeed.

Но автор, кажется, говорит, что вы должны пойти на реализацию этого в C/C++ вместо Python. Модуль Python rdrand работает примерно в 100 раз медленнее, чем генератор случайных чисел по умолчанию в Python, и примерно в 1000 раз медленнее, чем в Numpy (статья 5.2).